时间复杂度T(n)和渐进时间复杂度O(n)是什么,该如何计算?

提示：本文属于基础篇，内容过多，如果对此已有了解，可以直接阅读加粗文字

算法的效率 = 运行的时间 + 所需的存储空间 ，我们暂时不考虑存储空间，如何度量运行时间是本文讨论的内容，我们首先要考虑到影响算法执行时间的主要因素：算法选用的策略 、问题的规模。一个特定算法的运行时间，它是问题规模（通常用整数n表示）的函数。

总结：一个算法的语句执行的次数称为语句频度或者时间频度，表示为T(n)，n表示问题的规模；O(n)也是一个函数，它表示渐进时间复杂度，又叫大O表示法。

算法的量度记为：T(n)=O(f(n)) ——渐进时间复杂度

T(n)=O(f(n))的数学含义：存在两个常量C和N，当n≥N时，有T(n)≤C*f(n)

那么根据这个式子（过程不再描述）可以得出：

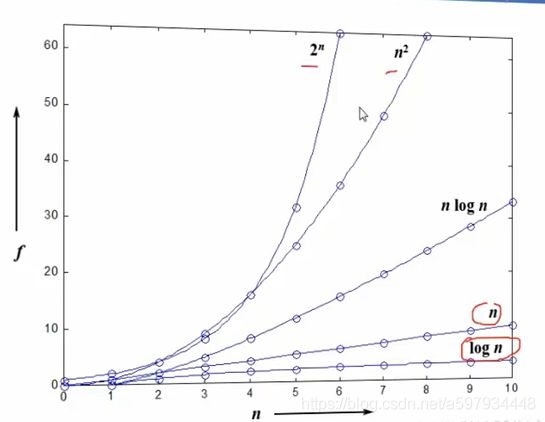
• 与T(n)相比,f(n)更为简洁,但依然会反映前者的增长趋势
• 低次项可忽略

总结：一般地，若T(n)是有关n的一个多项式,则f(n)可由T(n)中的最高此项去掉系数所得。

例：设有函数T(n)=3n²-n+4，请证明T(n)=O(n²)。

证明：因为存在C=6,N=1,对所有的n≥N,0≤3n²-n+4≤6n²都是成立的，所以由大O的定义可得T(n)=O(n²)。**

T(n)=O(f(n))，这是大O表示的渐进时间复杂度，它表示随着问题规模n的增长，算法执行时间的增长率是相同的，而且f(n)比T(n)更为简洁，f(n)由T(n)“去粗取精”（低次项忽略，常系数忽略）得到。

---

那么如何估算一个指定算法的时间复杂度呢？

算法 = 控制结构 + 原操作(对固有类型数据的操作)

算法的执行时间T(n) = 原操作重复执行的次数 或 原操作的语句频度

下面我们使用上面的结论估算一个算法的时间复杂度：

void mult(int a[],int b[],int &c[],int n){
//以二维数组村粗矩阵元素，c为a和b的乘积                 //语句频度
	for(i=1;i<=n;i++)								  //n+1
		for(j=1;j<=n;j++){							  //n(n+1)
			c[i,j]=0;								  //n² 关键操作
			for(k=1;k<=n;k++)						  //n²*(n+1)
				c[i,j] += a[i,k] * b[k,j];			  //n³ 关键操作
		}
}
                                                   
//所以T(n)=n³+n²=O(n³)    

结论：T(n) = 关键操作的语句频度 ，而关键操作往往就是算法中控制结构内最深层的原操作。

---

虽然我们用关键操作的频度来度量一个算法的操作时间，它所计算出来的量并不是时间量，而是一种增长趋势的量度，但是它与软硬件无关，只反映算法本身执行效率的优劣，所以是简便且有效的。下面我们一起来看例题：

//例题1，求下列程序段的时间复杂度
for(int i=1;i<=n;i=2*i)
	printf("i=%d\n",i); //关键操作

解题：设关键操作语句的执行次数为T(n)
有 2^T(n)≤n，所以T(n)≤log₂n，所以关键操作的语句频度是log₂n向下取整
T(n)=O(log₂n)=O(logn)

//例题2，求下列程序段的时间复杂度
for(int i=1;i<=n;i=2*i)
	for(int j=0;j<i;j++)
		printf("i=%4d",i); //关键操作

解题：设关键操作语句的执行次数为T(n)，那么有
T(n)=2⁰+2¹+2²+…+2^log₂n
这是一个几何级数，几何增速与末项的级数是相同的，所以这个算法的复杂度是T(n)=O(2^log₂n)=O(n)

归纳：
多项式时间算法的时间复杂度：
O(1) 指数时间算法的时间复杂度：
O(2ⁿ)n)

注意：线性集和对数集的增长趋势是比较平稳的，但是线性复杂度的算法不一定快于平方时间复杂度或者其他复杂度的算法，当问题规模n足够大才是恒成立的，所以时间复杂度比较时得看问题规模n的大小。