Dijkstra (迪杰斯特拉)算法c#实现方法

Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法

算法思想：

设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，

第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），

第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

(1) 初始时，S只包含起点s；U包含除s外的其他顶点，且U中顶点的距离为"起点s到该顶点的距离"[例如，U中顶点v的距离为(s,v)的长度，然后s和v不相邻，则v的距离为∞]。

(2) 从U中选出"距离最短的顶点k"，并将顶点k加入到S中；同时，从U中移除顶点k。

(3) 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其它顶点的距离；例如，(s,v)的距离可能大于(s,k)+(k,v)的距离。

(4) 重复步骤(2)和(3)，直到遍历完所有顶点。

         

 

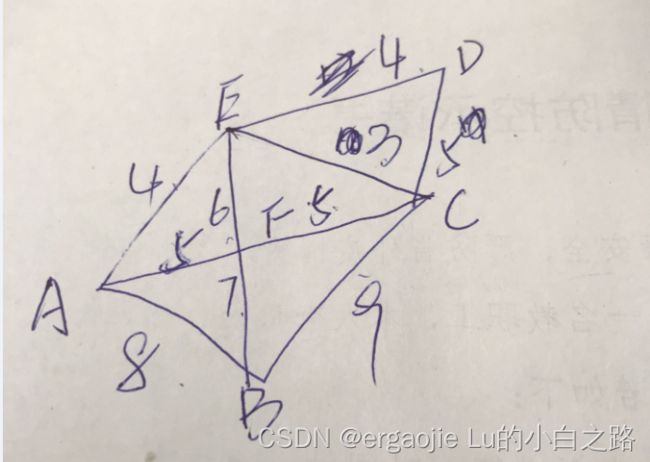
以这个图为例，求出A——》D的最短距离

代码如下：

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace 验证码
{
    public partial class 迪杰斯特拉 : Form
    {
        public 迪杰斯特拉()
        {
            InitializeComponent();
        }

        private void button1_Click(object sender, EventArgs e)
        {
            List str = new List();//建立List进行存储点
            str.Add("A");
            str.Add("B");
            str.Add("C");
            str.Add("D");
            str.Add("E");
            str.Add("F");//存储
            string[] str1 = { "A", "B", "C", "D", "E", "F" };//进行数组存储点（后期进行调用）
            int[,] intDis = new int[6, 6];//建立数组存储加权信息
            for (int i = 0; i < 6; i++)//全部写入10000（无穷）
            {
                for (int j = 0; j < 6; j++)
                {
                    intDis[i, j] = 10000;
                }
            }
            intDis[0, 4] = intDis[4, 0] = 4;
            intDis[0, 5] = intDis[5, 0] = 5;
            intDis[0, 1] = intDis[1, 0] = 8;
            intDis[4, 3] = intDis[3, 4] = 4;
            intDis[4, 5] = intDis[5, 4] = 6;
            intDis[2, 4] = intDis[4, 2] = 3;
            intDis[5, 1] = intDis[1, 5] = 7;
            intDis[5, 2] = intDis[2, 5] = 5;
            intDis[1, 2] = intDis[2, 1] = 9;
            intDis[3, 2] = intDis[2, 3] = 5;//对网络加权值进行构建
            string[] jihe = new string[6];//路径数组（以A为起点）
            jihe[0] = "A";
            jihe[1] = "B";
            jihe[2] = "C";
            jihe[3] = "D";
            jihe[4] = "E";
            jihe[5] = "F";
            List mListptS = new List();//点名S（最短）
            List mListptDisS = new List();//点距离（最短）
            List mListptU = new List();//点名U（临时存储）
            List mListptDisU = new List();//点距离U（临时存储）
            mListptS.Add("A");
            mListptDisS.Add(0);
            mListptU.Add("B");
            mListptDisU.Add(8);
            mListptU.Add("C");
            mListptDisU.Add(10000);
            mListptU.Add("D");
            mListptDisU.Add(10000);
            mListptU.Add("E");
            mListptDisU.Add(4);
            mListptU.Add("F");
            mListptDisU.Add(5);//按B,C,D,E,F进行存储，保证点与距离，str对应
            for (int i = 1; i < 6; i++)
            {
                jihe[i] = "A" +"==>"+ jihe[i];//确定起点为A
            }
            while (mListptU.Count != 0)//对U点集进行判断
            {
                int temp = 10000;//无穷距离
                int min = 10000;//无穷距离
                int suoyin = 0;//索引
                for (int i = 0; i < mListptU.Count; i++)
                {
                    if (temp > mListptDisU[i])
                    {
                        if (min > mListptDisU[i])//进行判断，选取与A距离最短的点
                        {
                            min = mListptDisU[i];
                            suoyin = i;
                        }
                    }
                }
                mListptS.Add(mListptU[suoyin]);//加入点集
                mListptDisS.Add(mListptDisU[suoyin]);//加入距离点集
                string ups = mListptU[suoyin];//选择的点，进行后期索引查找
                int upsd = 0;//在str中的索引值
                for (int i = 0; i < str.Count; i++)
                {
                    if (str[i] == ups)
                    {
                        upsd = i;//确定在str中的索引值，保持同步
                        break;
                    }
                }
                int updata = mListptDisU[suoyin];//点到确定点的距离

                for (int i = 1; i < mListptDisU.Count; i++)
                {
                    if (intDis[upsd, i] < 10000 || intDis[i, upsd] < 10000)//若不是无穷大进行下一步
                    {
                        if (mListptDisU[i - 1] > updata + intDis[i, upsd])//判断新路径是否比原路径短，若短进入下一步
                        {
                            mListptDisU[i - 1] = updata + intDis[i, upsd];//对新距离进行存储，注意索引值相对应
                            jihe[i] = mListptS[0] +"==>"+ str[upsd] + "==>"+str[i];//对路径进行存储
                        }
                    }
                }
                mListptU.Remove(mListptU[suoyin]);//删除点集中的选择点
                str.Remove(str[suoyin]);//删除对应的mListptU[]保持后面索引一致
            }
            string Finally = "D";
            for (int i = 1; i < 6; i++)//对A进行忽略（保证索引一致）
            {
                if (str1[i] == Finally)//选择要计算点的最短路径
                {
                    MessageBox.Show("距离："+mListptDisU[i - 1].ToString() + "|" +"路径："+ jihe[i]);//输出
                }
            }
        }
    }
    }

注：以窗体应用为例

输出的结果为到点的路径与长度。

实现成果：

 

下次见，拜拜！