排序算法-快速排序(Java实现)
快排是我们经常用到的经典排序算法之一,今天就来彻底的学习一下快排吧
文章目录
-
-
- 算法思想
- 代码实现-固定基准法
- 代码实现-随机选取基准法
- 代码实现-三分取中法
- 快排优化-小序列优化
- 快排优化-相同元素优化
- 非递归实现快排
- 最坏时间复杂度达到O(n log n)
-
算法思想
快速排序是指在待排序列中选取一个基准,然后把不比该基准大的放在基准的前面,把比该基准大的放在基准的后面,这样待排序列就被基准划分成了两个序列,对这两个序列再递归进行这样的操作,直到基准两边没有或者只有一个数字,最终就完成了排序。快排主要用到的算法思想是分治思想。
单纯的文字描述或许不能清晰的了解,通过一组例子来了解一下:
待排序列如下:
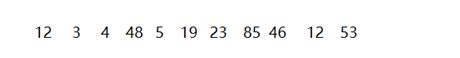
我们先来介绍第一种选取基准的方法:固定基准法
我们每次都选取当前序列的第一个数字为基准,当前的基准就是12,有两个指针,一个为low,指向当前序列的第一个数字,一个为high,指向当前序列的最后一个数字。先把基准拿出来(用temp保存一下),和high比较,如果high所指数字小了则把high数字放到low这里,low++,如果low小了则high–。继续比较low和high所指的数字,还有一种情况就是当空白位置在后面时(空白位置是指该数字放到其他地方,暂且认为是没有数字,其实这个地方是原来的数字,不过没意义了),temp和low比较,如果low小了,low++继续比较,如果high小了,把low的值拿出来给high,high–。
这样的文字虽然不太懂,确很容易能抽象出代码,我们可以先来看图片程序是如何跑的,然后再来读文字。

- 把12作为基准,拿出来

比较temp和high,high为53,high大了,所以high–,继续进行比较,high为12,交换没有意义,这块我们可以不写等于号,就可以继续往下比较了,high为46,high大了,high–,85大了,high–,23大了,high–,19大了,然后high指针指向了5。
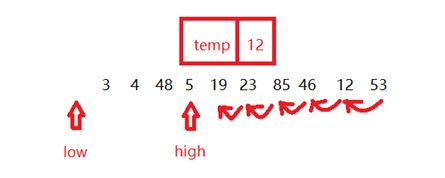
- 这时候,high比temp小,所以把5拿出来放到low的位置,low++
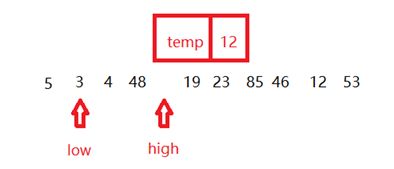
- 然后这次换low和temp比较,low为3比temp小,low++,low为4,比temp小,low++,low为48。
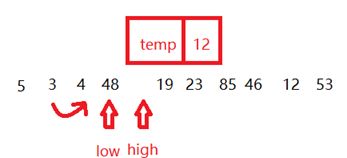
- 当low和temp比较后,发现temp小,所以把48放到high的位置,high–,这时候发现low和high相遇了。

- 当low和high重合的时候,把temp的值放到这里面来一趟划分就结束了,我们发现不比temp小的都在temp的后面,不比temp大的都在temp的前面。
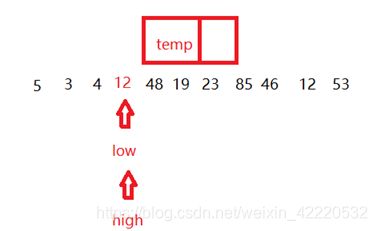
- 我们现在对 5 3 4 和 48 19 23 85 46 12 53这两个序列继续进行刚才的操作就会得到这样的结果

- 这就完成了第二次划分。5前面的4,3继续递归调用就会有序,后面没有数字所以不进行递归。48前面的序列和后面也继续重复这个操作。最终整个序列就会有序了。
代码实现-固定基准法
public static void quickSort(int []array) {
sort(array,0,array.length-1);
}
public static void sort(int[] array,int low,int high) {
int par = partition(array,low,high);
if(par > low+1) {
sort(array,low,par-1);
}
if(par < high-1) {
sort(array,par+1,high);
}
}
public static int partition(int[] array,int low,int high) {
int pivot = array[low];
while(low < high) {
while(pivot < array[high] && low < high) {
high--;
}
if(low >= high) {
break;
} else {
array[low] = array[high];
low++;
}
while(pivot > array[low] && low < high) {
low++;
}
if(low >= high) {
break;
} else {
array[high] = array[low];
high--;
}
}
array[low] = pivot;
return low;
}
排序属性分析:
- 从排序的过程来看,该过程一直在跳跃交换数字,所以快排是不稳定的。
- 快排使用了分治的思想,所以如果待排序列是正序或者逆序,那么快排每次得到的序列都是比上一层递归少一个元素的序列,那么时间复杂度就为O(n2),不过一般情况下,平均下来的时间复杂度是O(n log n),最好情况下,就是基准选取的非常合理,把待排序列平等划分,这样的话是最好的。
如何把基准划分的非常合理呢?我们刚才上面的思路是固定基准法,也就是默认把一个序列的第一个元素当做基准,但是如果选取的序列第一个很大概率是最小的,那么选取的基准肯定是非常不合理的,所以引入第二种选取基准的方法:随机选取基准法
代码实现-随机选取基准法
随机选取基准法的思路很简单,我们只需要在待排序列中拿到一个随机下标,然后把该下标对应的元素与第一个下标对应的元素交换,其他代码不变,就可以实现该功能了
具体一点来说:我们要做的就是在这个序列中找到一个随机的数字,和low作交换,代替low成为基准,这趟划分中,这个随机的数字就是基准。所以我们只需要在partition调用之前,写一个函数交换一下就可以了。
public static void swap(int[] array,int ran,int low) {
int temp = array[ran];
array[ran] = array[low];
array[low] = temp;
}
public static void sort(int[] array,int low,int high) {
//生成一个在low到high范围内的数字下标
Random random = new Random();
int ran = random.nextInt(high-low)+low;
//交换该下标和第一个元素下标
swap(array,ran,low);
int par = partition(array,low,high);
if(par > low+1) {
sort(array,low,par-1);
}
if(par < high-1) {
sort(array,par+1,high);
}
}
partition函数还是不变的
继续思考,随机选取基准法具有很大的随机性,如果本来第一个元素是一个比较好的基准,但是随机数选择到的是最小的,那么交换完反而降低了效率,这种可能性是存在的,因为存在很大的随机性
如何想办法解决这个问题呢?就引入了第三种选取基准的方法:三分取中法
代码实现-三分取中法
三分取中是指从待排序列中选取下标为 (low+high)/2 的下标定位mid,然后我们通过比较low,high,和mid的值,对这三个数实现换位
换位完的顺序是array[high]>array[low]>array[mid]
同样我们只需要在代码中写一个函数
public static void selectMid(int[] array,int low,int high) {
int mid = (low + high)/2;
//array[high]>array[low]>array[mid]
int temp = 0;
if(array[high] < array[mid]) {
temp = array[high];
array[high] = array[mid];
array[mid] = temp;
}
if(array[high] < array[low]) {
temp = array[high];
array[high] = array[low];
array[low] = temp;
}
if(array[low]<array[mid]) {
temp = array[mid];
array[mid] = array[low];
array[low] = temp;
}
}
public static void sort(int[] array,int low,int high) {
//调用三分取中函数
selectMid(array,low,high);
int par = partition(array,low,high);
if(par > low+1) {
sort(array,low,par-1);
}
if(par < high-1) {
sort(array,par+1,high);
}
}
快排优化-小序列优化
当递归至待排序列剩下N=10个数时,快排就没有插入排序的优势明显,所以我们在待排序列小于等于10的时候,使用插入排序。
if (high - low <= 10)
{
InsertSort(arr,low,high);
return;
}
快排优化-相同元素优化
在第一个例子中发现,和基准相同的元素我们没有做任何处理,跳过了这个数字。我们完全可以把和基准相同的元素聚集在基准旁边,然后重新定义下一次递归的范围,这样算法效率会高很多。
举个例子:
待排序列如下:

知道了功能后,如何去实现这个功能呢?
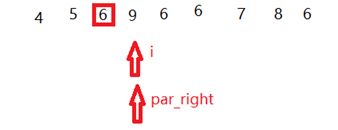
我们定义两个指针分别为par_left,par_right,让他们分别指向基准的左边和右边第一个元素,定义另外一个指针负责遍历。以par_right举例,就是循环右边的所有元素,如果遇到6,就交换par_right和遍历指针的值,然后par_right往后移动一位,通过画图来理解一下:
- 判断i是否和基准相等,不相等,i往后继续遍历。
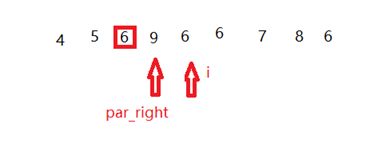
- 发现现在i和基准相等了,所以将i和par_right交换,i++,par_right++,如下图
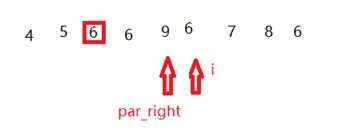
- i还是6,i和par_right继续进行交换,i++,par_right++
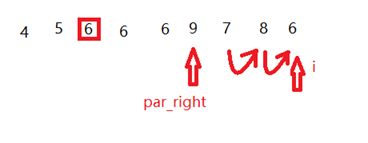
- i和基准不相等,一直往后移动,直到又出现了6,完成交换,这样右边的所有6都挪到了基准的右边,左边的同理。
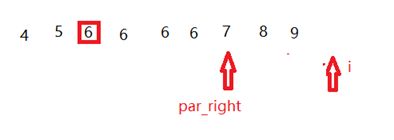
看一下代码实现:
public static void sort(int[] array,int low,int high) {
int par = partition(array,low,high);
//每次划分后把与基准相同的元素聚集到基准旁边,然后重新定义范围再次进行递归
int par_left = Foucs_Same_elem(array,low,high,par)[0];
int par_right = Foucs_Same_elem(array,low,high,par)[1];
if(par_left >= low+1) {
sort(array,low,par_left);
}
if(par_right <= high-1) {
sort(array,par_right,high);
}
}
public static int[] Foucs_Same_elem(int[] array,int low,int high,int par) {
int par_left = low-1,par_right = high+1;
if(par-1 >= low) {
par_left = par-1;
}
if(par+1 <= high) {
par_right = par+1;
}
for (int i = par_right; i <= high ; i++) {
if(array[i] == array[par]) {
if(i != par_right) {
swap(array,par_right,i);
par_right++;
}
}
}
for (int i = par_left; i >= 0 ; i--) {
if(array[i] == array[par]) {
if(i != par_left) {
swap(array,par_left,i);
par_left--;
}
}
}
return new int[]{par_left,par_right};
}
非递归实现快排
无论是递归还是非递归,我们的partition函数是不变的,就是我们划分返回基准的函数是不变的,不过是非递归的时候用栈模拟递归的过程,把每次排序low和high存储到栈里面,用的时候出栈,产生新的low和high的时候入栈,一直运行到栈为空,这样就把所有的序列都进行了划分。
举个例子:

我们先对待排序列进行一次划分,这里我们就用固定基准法来说明
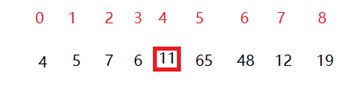
我们把0,3,5,8压栈,然后开始进行循环
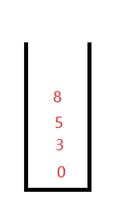
开始循环,8和5出栈,这个时候一定要注意哪个是low,哪个是high,然后根据5和8进行划分
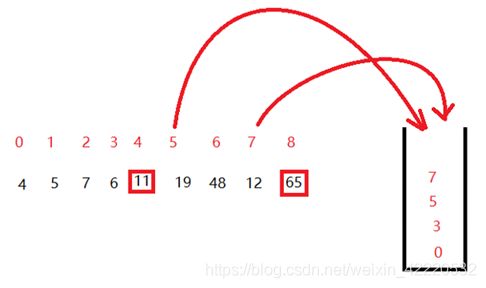
然后我们把5和7入栈,对5和7进行划分

发现6的左右都只有一个数字,默认有序了,没有什么可以入栈的,所以就继续下次循环,从栈中取出0,3进行划分
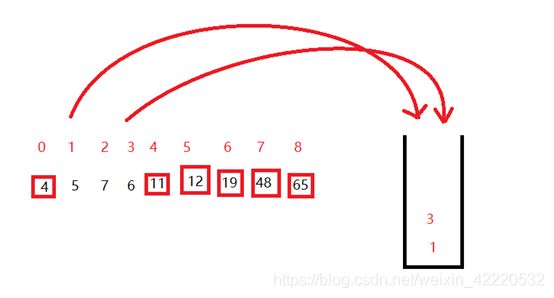
把1,3入栈,然后取出1,3,再次进行划分
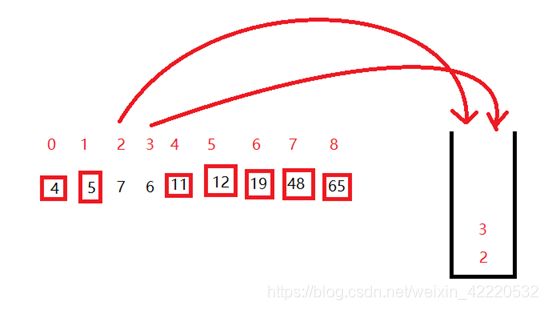
5有序后,5后面剩下2号和3号,所以2号和3号入栈
继续循环,2和3出栈,进行划分

2号只有一个数字,默认有序,继续出栈,发现栈为空,所以循环结束,排序也就完成了。
代码实现:
public static void quickSort(int []array) {
//建造一个模拟栈
int[] stack = new int[array.length];
//定义栈的有效数字个数
int size = 0;
int par = partition(array,0,array.length-1);
if(par - 1 > 0) {
stack[size++] = 0;
stack[size++] = par-1;
}
if(par + 1 < array.length-1) {
stack[size++] = par+1;
stack[size++] = array.length-1;
}
while(size > 0) {
int high = stack[--size];
int low = stack[--size];
par = partition(array,low,high);
if(par - 1 > low) {
stack[size++] = low;
stack[size++] = par-1;
}
if(par + 1 < high) {
stack[size++] = par+1;
stack[size++] = high;
}
}
}
public static int partition(int[] array,int low,int high) {
int pivot = array[low];
while(low < high) {
while(pivot < array[high] && low < high) {
high--;
}
if(low >= high) {
break;
} else {
array[low] = array[high];
low++;
}
while(pivot > array[low] && low < high) {
low++;
}
if(low >= high) {
break;
} else {
array[high] = array[low];
high--;
}
}
array[low] = pivot;
return low;
}
最坏时间复杂度达到O(n log n)
待更新… …