数据结构与算法 —— 最短路径Dijkstra算法（迪杰斯特拉）详细图解以及python实现

目录

前言

1. 介绍

2. 加权图

2.1 概念

3. 最短路径 -- Dijkstra 算法

3.1 历史

3.2 Dijkstra 算法的基本思路

3.3 Dijkstra 算法图解

4.  python中dijkstra算法的实现

5. 总结 

---

前言

前两章我们讲到了关于图的基本知识，和广度/深度优先搜索。

本章，我们将介绍加权图和最短路径的相关知识。

---

1. 介绍

最短路径是图论中常见问题。

最短路径是指在一个图中找到两个节点之间的最短路径。

最短路径算法常见的有 floyd算法（弗洛伊德算法）和 dijkstra算法（迪杰斯特拉）。本文只介绍dijkstra算法。
最短路径运用非常广泛，比如在导航系统中，确定两个地点间哪条路线最短；在网络路由中，路由器需要找到最短路径来转发数据包。

---

2. 加权图

2.1 概念

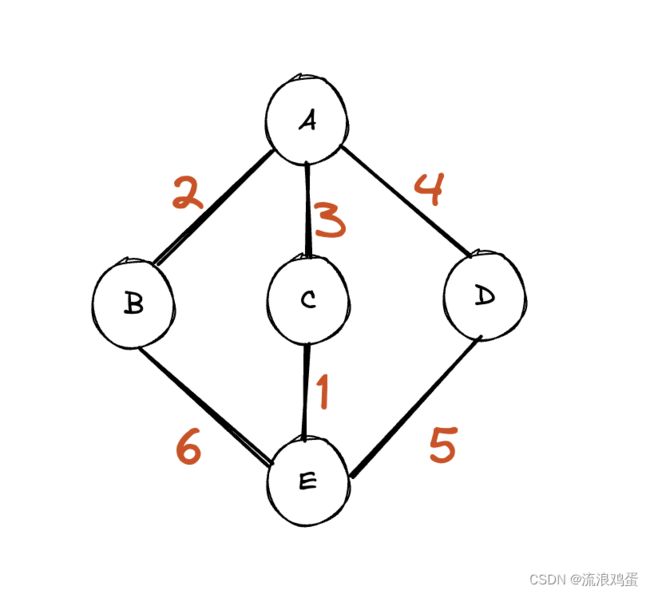
加权图是指每条边都带有权重的图。每个边的权重可以表示两个顶点之间的距离、成本或任何其他可以量化的指标。实际上，边的权重可以为负数，但是本章只介绍最短路径中的dijkstra算法且这种算法的前提条件就是权重不能为负数，所以不将负数的权重拓展到本文。

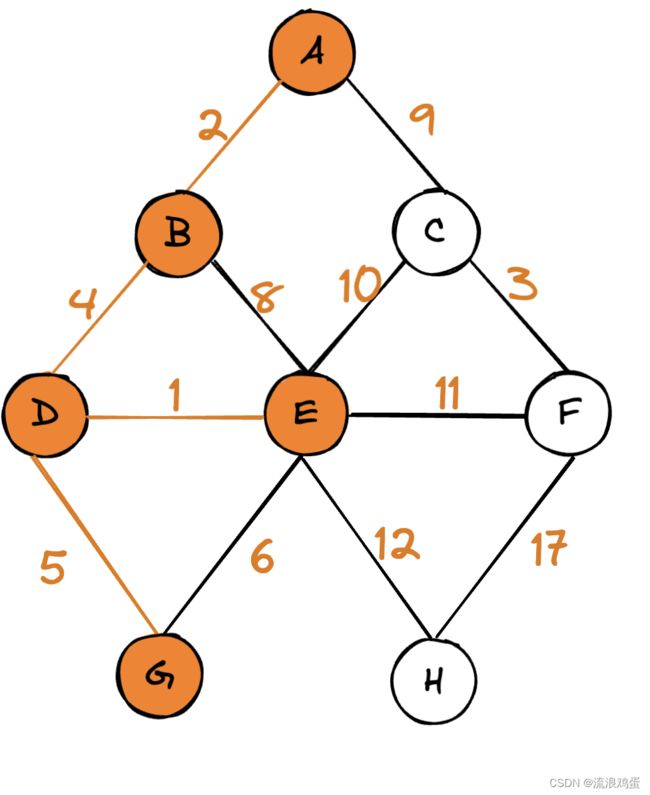
下面的加权图中，每一个红色的数字都代表着那条边的权重。

---

3. 最短路径 -- Dijkstra 算法

3.1 历史

这个算法由荷兰杰出计算机科学家、软件工程师艾兹赫尔·戴克斯特拉 (Edsger W. Dijkstra)（1930年5月11日~2002年8月6日）发明。他是计算机先驱之一，与高德纳（Donald Ervin Knuth）并称为我们这个时代最伟大的计算机科学家。

从 Rotterdam 到 Groningen 的最短路线是什么？我花了大概 20 分钟时间设计了这个寻找最短路径的算法。一天早上我正和我年轻的未婚妻在 Amsterdam 逛街，觉得有点累了，我们就坐在咖啡厅的露台上喝了一杯咖啡，我在想是否能够解决这个问题，然后，我设计出了这个最短路径算法。我说过，这是一个 20 分钟的设计。事实上，三年之后的 1959 年它才被发布，现在看来依然很不错，其原因之一是我当时设计的时候没有纸和笔，从而不得不极力避免所有可避免的复杂性。最终，令我惊讶的是，这个算法成为了我成名的基石之一。

节选自文章《An interview with Edsger W. Dijkstra》

3.2 Dijkstra 算法的基本思路

首先将起始节点的距离标记为0，其他节点的距离因为还不确定所以先需要标记为无穷大。

然后，在图中找到距离起始节点最近的节点，更新其相邻节点的距离，距离为从起始节点到该节点的距离加上该节点到相邻节点的距离。

不断循环此过程，直到所有节点都被访问过。

这就是Dijkstra 算法的基本思路。

3.3 Dijkstra 算法图解

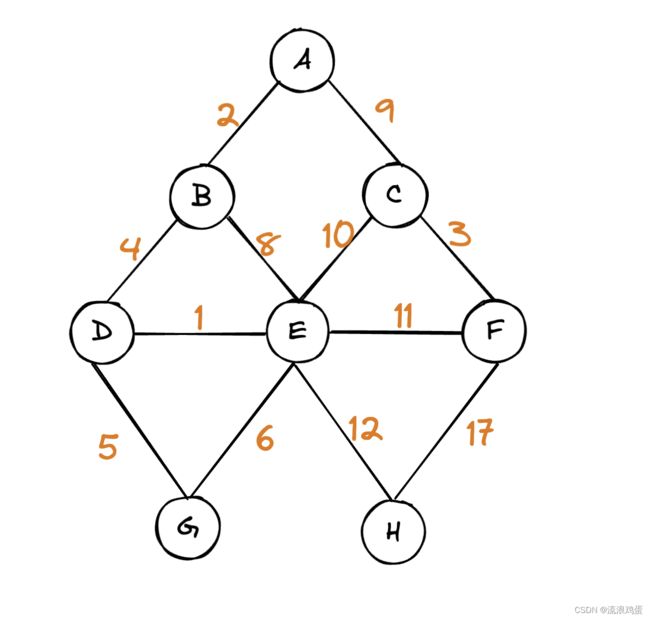
在下面这个图的基础上，我们可以一步一步来分析Dijkstra 算法的过程。

我们的目的是用此算法找到节点D到任意其他节点的最短路径。

1. 首先我们创建一个表格来记录节点D到所有节点的距离（自身为0，其余初始化为无穷大），还需要记录最短路径中每个节点的先驱节点（初始化为空）。最后需要一个flag去标记已经访问过的节点（初始化为F）。

节点	Flag	距离	先驱节点
A	F	∞
B	F	∞
C	F	∞
D	F	0
E	F	∞
F	F	∞
G	F	∞
H	F	∞

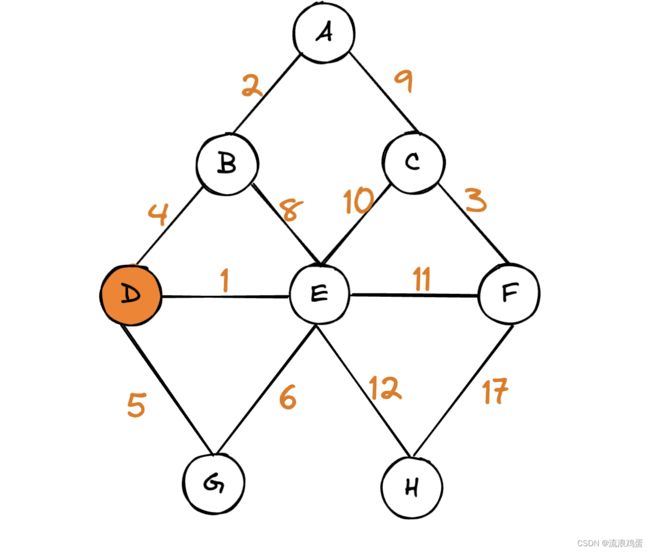
2. 检查所有未标记节点中距离最短的节点，就是节点D，将其加入最短路径中，并标记。 

节点	Flag	距离	先驱节点
A	F	∞
B	F	∞
C	F	∞
D	T	0
E	F	∞
F	F	∞
G	F	∞
H	F	∞

3. 更新经过节点D的相邻节点距离到起始节点的距离，也就是D-B，D-E，D-G的距离，分别是4，1，5，同时使节点D作为他们的先驱节点。

节点	Flag	距离	先驱节点
A	F	∞
B	F	4	D
C	F	∞
D	T	0
E	F	1	D
F	F	∞
G	F	5	D
H	F	∞

4. 检查所有未标记节点中距离最短的节点，就是节点E，将其加入最短路径中，并标记。

节点	Flag	距离	先驱节点
A	F	∞
B	F	4	D
C	F	∞
D	T	0
E	T	1	D
F	F	∞
G	F	5	D
H	F	∞

5.  更新经过节点E的相邻节点到起始节点的距离，也就是D-E-B，D-E-C，D-E-F，D-E-G和D-E-H的距离，分别是9，11，12，7,13。但是因为D-B和D-G的路径在上一步已经更新过了，并且距离要小于D-E-B和D-E-G的距离，所以不更新节点B和节点G的距离，更新节点C，F和H的距离，同时使节点E作为他们的先驱节点。

节点	Flag	距离	先驱节点
A	F	∞
B	F	4	D
C	F	11	E
D	T	0
E	T	1	D
F	F	12	E
G	F	5	D
H	F	13	E

6.  检查所有未标记节点中距离最短的节点，就是节点B，将其加入最短路径中，并标记。

节点	Flag	距离	先驱节点
A	F	∞
B	T	4	D
C	F	11	E
D	T	0
E	T	1	D
F	F	12	E
G	F	5	D
H	F	13	E

7. 更新经过节点B的相邻节点到起始节点的距离，也就是D-B-A，距离为6，同时使节点B作为他的先驱节点。 

节点	Flag	距离	先驱节点
A	F	6	B
B	T	4	D
C	F	11	E
D	T	0
E	T	1	D
F	F	12	E
G	F	5	D
H	F	13	E

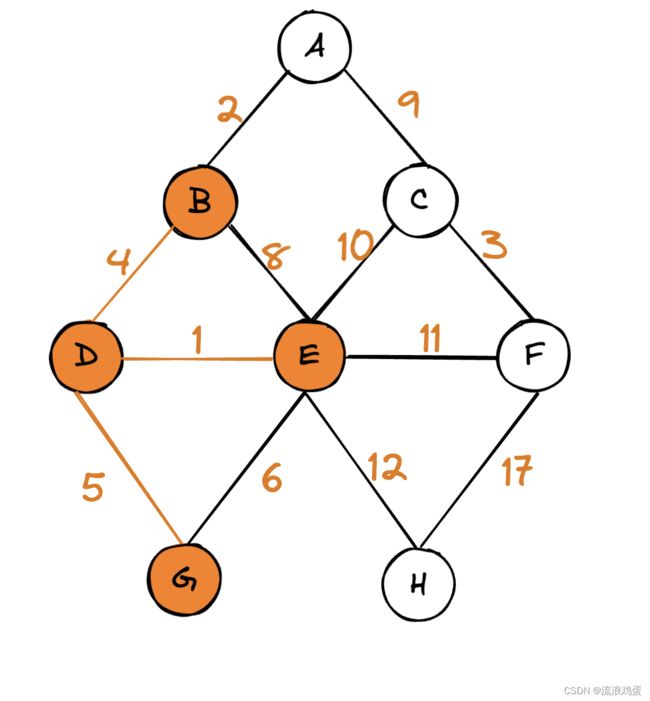
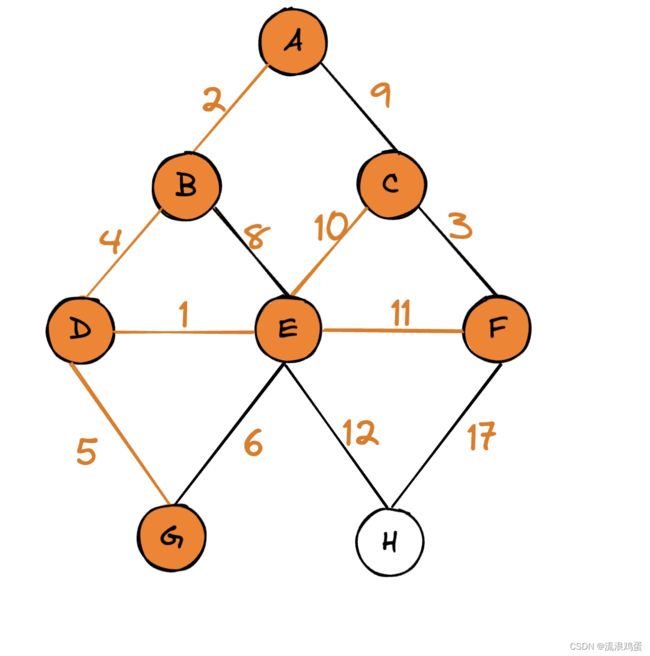
8.  检查所有未标记节点中距离最短的节点，就是节点G，将其加入最短路径中，并标记。

节点	Flag	距离	先驱节点
A	F	6	B
B	T	4	D
C	F	11	E
D	T	0
E	T	1	D
F	F	12	E
G	T	5	D
H	F	13	E

9.   更新经过节点G的相邻节点到起始节点的距离，也就是D-G-E，距离为11，但是因为之前保存过D-E的距离为1，很明显D-E的距离要更近一些，所以不更新表格。

10. 检查所有未标记节点中距离最短的节点，就是节点A，将其加入最短路径中，并标记。

节点	Flag	距离	先驱节点
A	T	6	B
B	T	4	D
C	F	11	E
D	T	0
E	T	1	D
F	F	12	E
G	T	5	D
H	F	13	E

11.  更新经过节点A的相邻节点到起始节点的距离，也就是D-B-A-C，距离为15，但是因为之前保存过D-E-C的距离为11，D-E-C的距离要近于D-B-A-C，所以不更新表格。

12.  检查所有未标记节点中距离最短的节点，就是节点C，将其加入最短路径中，并标记。

节点	Flag	距离	先驱节点
A	T	6	B
B	T	4	D
C	T	11	E
D	T	0
E	T	1	D
F	F	12	E
G	T	5	D
H	F	13	E

13. 更新经过节点C的相邻节点到起始节点的距离，也就是D-E-C-F，距离为14，但是因为之前保存过D-E-F的距离为12，D-E-F的距离要近于D-E-C-F，所以不更新表格。 

14. 检查所有未标记节点中距离最短的节点，就是节点F，将其加入最短路径中，并标记。

节点	Flag	距离	先驱节点
A	T	6	B
B	T	4	D
C	T	11	E
D	T	0
E	T	1	D
F	T	12	E
G	T	5	D
H	F	13	E

15. 更新经过节点F的相邻节点到起始节点的距离，也就是D-E-F-H，距离为29，但是因为之前保存过D-E-H的距离为13，D-E-H的距离要近于D-E-F-H，所以不更新表格。

16.   检查所有未标记节点中距离最短的节点，就是节点H，将其加入最短路径中，并标记。

节点	Flag	距离	先驱节点
A	T	6	B
B	T	4	D
C	T	11	E
D	T	0
E	T	1	D
F	T	12	E
G	T	5	D
H	T	13	E

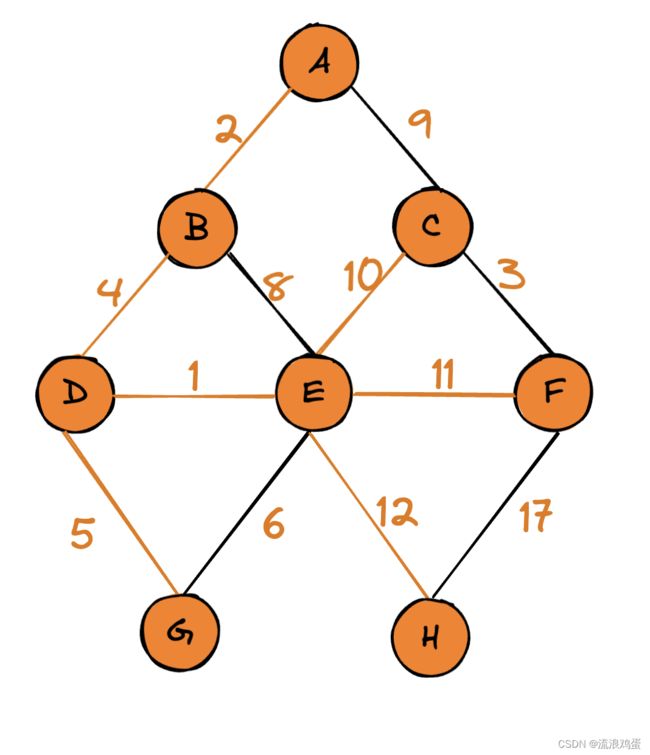
17. 算法结束，此时我们拥有了从出发点D到任意一个节点的距离以及路径。最短路径可以根据先驱节点倒推出来，比如从D到H的最短距离为13，最短路径为D-E-H。

节点	Flag	距离	先驱节点
A	T	6	B
B	T	4	D
C	T	11	E
D	T	0
E	T	1	D
F	T	12	E
G	T	5	D
H	T	13	E

最短距离：看节点H，发现与起始点D的最短距离为13。
最短路径：看H的先驱节点，发现是E，在看E的先驱节点，发现是D。那么，从D到H的最短路径就是D-E-H了。 

---

4.  python中dijkstra算法的实现

import sys

def dijkstra(graph, start_node):
    unvisited_nodes = {node: sys.maxsize for node in graph}  # 初始化所有节点距离为无穷大
    unvisited_nodes[start_node] = 0  # 起始节点距离为0
    shortest_paths = {start_node: (0, [])}  # 起始节点的路径和距离

    while unvisited_nodes:
        current_node = min(unvisited_nodes, key=unvisited_nodes.get)  # 找到未访问节点中距离最小的节点
        current_distance = unvisited_nodes[current_node]

        for neighbor, distance in graph[current_node].items():
            if neighbor not in unvisited_nodes: continue  # 已访问过的节点跳过
            new_distance = current_distance + distance
            if new_distance < unvisited_nodes[neighbor]:  # 如果找到更短路径，更新
                unvisited_nodes[neighbor] = new_distance
                shortest_paths[neighbor] = (new_distance, shortest_paths[current_node][1] + [current_node])  # 更新路径和距离

        unvisited_nodes.pop(current_node)  # 当前节点已访问过，从未访问节点中删除

    return shortest_paths  # 返回最短路径和距离

# 测试Dijkstra算法
if __name__ == "__main__":
    graph = {
        'A': {'B': 2, 'C': 9},
        'B': {'A': 2, 'D': 4, 'E': 8},
        'C': {'A': 9, 'E': 10, 'F': 3},
        'D': {'B': 4, 'E': 1, 'G': 5},
        'E': {'B': 8, 'C': 10, 'D': 1, 'F': 11, 'G': 6, 'H': 12},
        'F': {'C': 3, 'E': 11, 'H': 17},
        'G': {'D': 5, 'E': 6},
        'H': {'E': 12, 'F': 17},
    }
    start_node = 'D'
    shortest_paths = dijkstra(graph, start_node)
    print(shortest_paths)

首先我创建了一个上面举例子的图，然后设置顶点D为起始顶点。

运行上面代码之后会打印出：

{'D': (0, []), 'B': (4, ['D']), 'E': (1, ['D']), 'G': (5, ['D']), 'C': (11, ['D', 'E']), 'F': (12, ['D', 'E']), 'H': (13, ['D', 'E']), 'A': (6, ['D', 'B'])}

我们可以很明显找到从D到任意一个顶点的最短路径和距离。

---

5. 总结 

Dijkstra算法是非常经典的最短路径算法，这种算法可以找到起始顶点与图中任意一个顶点的最短路径。但是其也有限制，图的权重必须不能有负数。如果图的权重带有负数，则需要使用Bellman-ford算法，如果想要确定任意两点的最短路径，则需要使用floyd算法。

---

ps. 本来打算把最小生成树也在这一章总结的，但是最近学校事情比较多，只能往后拖一拖了TOT 

希望大家能从这篇文章中对Dijkstra算法有更清晰的了解，如果我有什么地方讲的不对，欢迎大家指出！