数据结构初阶--栈和队列
一、栈
栈的概念及结构
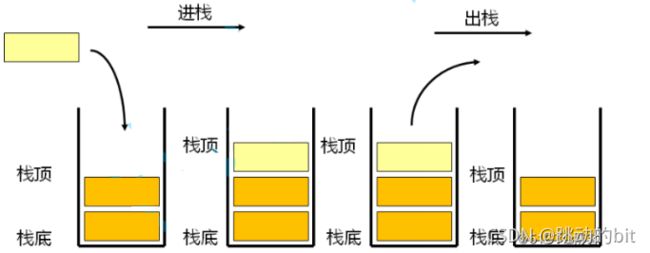
栈:一种特殊的线性表,其只允许在固定的一端插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO (Last In First Out) 的原则;同时对于栈来说,一种入栈顺序对应多种出栈顺序
栈有两个经典的操作
1️⃣ 压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
2️⃣ 出栈:栈的删除操作叫做出栈。出数据也在栈顶 。
栈的实现
⛅注:对于链式表
如果用尾做栈顶,尾插尾删,要设计成双向链表,否则要找尾节点前一个链表,删除效率很低
如果用头做栈顶,头插头删,就可以设计成单链表
这里对于栈的实现我们既可以选择数组也可以和选择链表两者的效率都差不多,但是还是建议使用数组
因为存储数据时,数组申请一次所得到的空间大于链表,数据存储速度更快。而链表申请一次存一次
因为数组栈支持随机访问,故它的头删尾删效率更高
创建栈
静态栈的创建:
typedef int STDataType;
typedef N 10;
typedef struct Stack
{
STDataType a[N];
int top;//栈顶的位置
}ST;动态栈的创建:
typedef int STDataType;
typedef struct Stack
{
STDataType* a;
int top;//栈顶
int capacity;//容量空间大小
}ST;初始化:
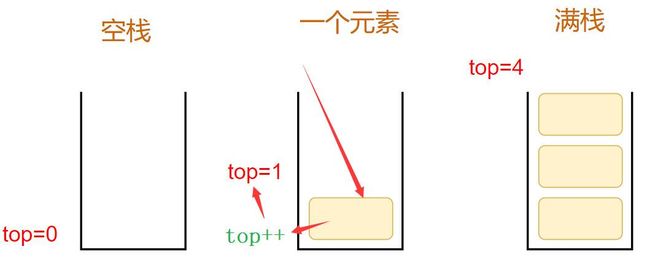
top为0的初始化:
void StackInit(ST* ps)
{
assert(ps);
ps->a = NULL;
ps->top = 0;
ps->capacity = 0;
}对于top 初始化为0,其实就是每次栈顶添加新元素时,都是先进行赋值,再top++,并且还需要对栈满进行判断
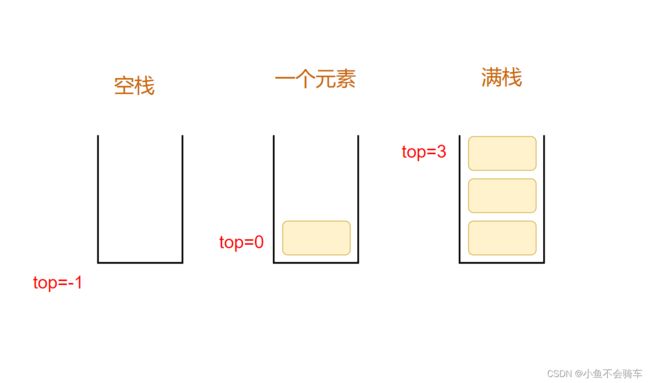
top为-1的初始化:
void StackInit(ST* ps)
{
assert(ps);
ps->a = NULL;
ps->top = -1;
ps->capacity = 0;
}当我的top初始化为-1时,由于我们添加元素需要从0下标开始添加,所以我们需要先top++,再赋值,此时我们的top记录的就是栈顶元素的下标
入栈/插入:
初识化好栈后,就可以把元素压到栈里了,因为栈是一个简化版的顺序表,从下标为零开始插入元素,可以理解为刚插入的元素就是在顺序表的最后边(把顺序表逆时针竖过来 理解成栈的顶),然后元素个数自增1,当元素个数等于栈的容量时就要进行扩容了,这里是两倍两倍地扩容,以此来实现栈。
实现的代码非常简单,只有短短几行。
void StackPush(ST* ps, STDatatype x)
{
assert(ps);
checkCapacity(ps);
ps->a[ps->top] = x;
ps->top++;
}
入栈就是增加元素,每次增加一个元素,top自加1,增加的元素多了就会使栈的容量不足,这是就要进行扩容了,这里写了一个checkCapacity的函数来检查是否需要扩容,需要则该函数会自动完成扩容。
void checkCapacity(ST* ps)
{
assert(ps);
//检查空间,满了就增容
if (ps->top == ps->capacity)
{
//第一次开辟空间容量为4,其它次容量为当前容量*2
int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
//第一次开辟空间,a指向空,realloc的效果同malloc
STDataType* newStack =(STDataType*) realloc(ps->a, sizeof(STDataType) * newCapacity);
//检查realloc
//realloc失败
if (newStack == NULL)
{
printf("realloc fail\n");
exit(-1);
}
//realloc成功
ps->a = newStack;
ps->capacity = newCapacity;
}
}思想:如果栈的容量和元素个数相等了就要进行扩容,因为初始化的时候是设置的容量和元素个数都为0,a为空,那么扩容是就要判断容量是否为0,如果为0就先开辟4个元素的空间供栈使用,否则就按照原来容量的两倍进行扩容。扩容失败就结束程序,成功就把开辟的空间的地址赋值给原来指向存储数据空间的指针a,扩容完成后栈的容量变为原来二倍。
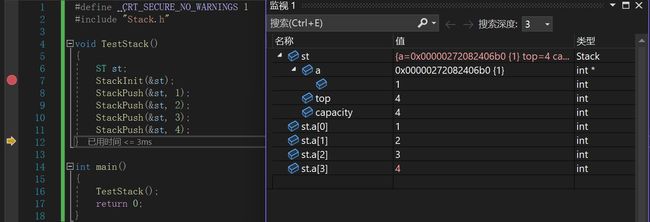
注:监视时,要观察全局的压栈出栈对应的x情况,可以用st.a[下标]的方法
判空:
直接返回元素个数是否等于0即可
写法一:
bool StackEmpty(ST* ps)
{
assert(ps);
/* if (ps->top == 0)
{
return true;
}
else
{
return false;
}
*/
//等于0是真,否则为假
return ps->top == 0;
}写法二:
bool StackEmpty(ST* ps)
{
assert(ps);
if (ps->top == 0)
{
return true;
}
else
{
return false;
}
}出栈/删除:
实现了入栈就要实现出栈,既然压栈和出栈是类似往弹夹里压子弹出子弹,那么出栈就是把最上面的元素拿出来即可,上面说了栈是一个简单的顺序表,入栈是把元素依次往后放,最后边的元素就是栈顶的元素,我们出栈就是拿栈顶的元素出来,也就是把顺序表最后边的元素拿出来(对应下标为顺序表(或栈 都是一样的 栈就是阉割了的顺序表)的元素个数减1),然后让栈的元素个数自减即可完成出栈操作。
这里是直接让栈的元素个数自减1,这样就让出栈的元素的下面一个元素就是新的栈顶元素了
注意:这里出栈的条件必须是栈的元素个数大于零!!!
void StackPop(ST* ps)
{
assert(ps);
//删除的话得保证指向的空间不为空
assert(!StackEmpty(ps));//看解释1,解释2
//删除
--ps->top;
}1️⃣也可以写成assert(ps->top>0);
2️⃣确保我们在出栈/删除的时候,top>0。如果没有这一步,万一我们删狠了,把它删到top=-100去了,到时候咱们再打印可就要越界访问报错了
长度:
STDataType StackSize(ST* ps)
{
assert(ps);
//此时的top就是长度
return ps->top;
}栈顶:
STDatatype StackTop(ST* ps)
{
assert(ps);
//找栈顶的话得保证指向的空间不为空
assert(!StackEmpty(ps));//等效于assert(ps->top >0);
//此时的top-1就是栈顶数据
return ps->a[ps->top - 1];
}销毁:
我们把元素入栈是存放在a指向的空间中的,入栈的过程中可能有多次扩容,我们在销毁栈的时候就把这块空间释放掉,把指向这块空间的指针a置空防止出现野指针,然后让元素个数和容量都为空即可。
void StackDestory(ST* ps)
{
assert(ps);
//a为真代表它指向动态开辟的空间
if (ps->a)
{
free(ps->a);
}
ps->a = NULL;
ps->top = 0;
ps->capacicy = 0;
}打印:
while (!StackEmpty(st))//不为空,则继续
{
printf("%d ", StackTop(st));//打印当前栈顶
StackPop(&st);//把当前栈顶给删掉,得到新栈顶
}完整代码
这里需要三个文件
1️⃣ Static.h,用于函数的声明
2️⃣ Static.c,用于函数的定义
3️⃣ Test.c,用于测试函数
Stack.h
#pragma once
//头
#include
#include
#include
#include
//结构体
typedef int STDatatype;
typedef struct Stack
{
STDatatype* a; //指向动态开辟的空间
int top; //栈顶
int capacicy; //容量
}ST;
//函数
//注意链表和顺序表我们写Print,但是栈不写,因为如果栈可以Print的话,就不符合后进先出了
//初始化
void StackInit(ST* ps);
//插入
void StackPush(ST* ps, STDatatype x);
//判空
bool StackEmpty(ST* ps);
//删除
void StackPop(ST* ps);
//长度
int StackSize(ST* ps);
//栈顶
STDatatype StackTop(ST* ps);
//打印
void Print(ST* ps);
//销毁
void StackDestory(ST* ps);
Stack.c
#include"Stack.h"
void StackInit(ST* ps)
{
assert(ps);
//初始化
ps->a = NULL;
ps->top = 0;
ps->capacicy = 0;
}
void StackPush(ST* ps, STDatatype x)
{
assert(ps);
//检查空间,满了就增容
if (ps->top == ps->capacicy)
{
//第一次开辟空间容量为4,其它次容量为当前容量*2
int newcapacity = ps->capacicy == 0 ? 4 : ps->capacicy * 2;
//第一次开辟空间,a指向空,realloc的效果同malloc
STDatatype* tmp = realloc(ps->a, sizeof(STDatatype) * newcapacity);
//检查realloc
//realloc失败
if (tmp == NULL)
{
printf("realloc fail\n");
exit(-1);
}
//realloc成功
ps->a = tmp;
ps->capacicy = newcapacity;
}
//插入数据
ps->a[ps->top] = x;
ps->top++;
}
bool StackEmpty(ST* ps)
{
assert(ps);
//等于0是真,否则为假
return ps->top == 0;
}
void StackPop(ST* ps)
{
assert(ps);
//删除的话得保证指向的空间不为空
assert(!StackEmpty(ps));
//删除
--ps->top;
}
int StackSize(ST* ps)
{
assert(ps);
//此时的top就是长度
return ps->top;
}
STDatatype StackTop(ST* ps)
{
assert(ps);
//找栈顶的话得保证指向的空间不为空
assert(!StackEmpty(ps));
//此时的top-1就是栈顶数据
return ps->a[ps->top - 1];
}
//打印
void Print(ST* ps)
{
assert(ps);
while (!Empty(ps))
{
printf("%d ", STTop(ps));
STPop(ps);
}
}
void StackDestory(ST* ps)
{
assert(ps);
//a为真代表它指向动态开辟的空间
if (ps->a)
{
free(ps->a);
}
ps->a = NULL;
ps->top = 0;
ps->capacicy = 0;
}
Test.c
#include"Stack.h"
int main()
{
ST st;
//初始化
StackInit(&st);
//插入+删除
StackPush(&st, 1);
StackPush(&st, 2);
StackPush(&st, 3);
StackPush(&st, 4);
StackPush(&st, 5);
StackPop(&st);
StackPop(&st);
//长度
StackSize(&st);
//栈顶
StackTop(&st);
//打印
Print(&st);
//销毁
StackDestory(&st);
return 0;
}
二、队列
队列的概念及结构
相比栈,队列的特性和栈是相反的。
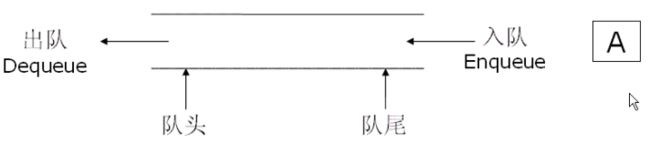
它只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO (First In First Out) 的特性。
入队列:进行插入操作的一端称为队尾;出队列:进行删除操作的一端称为队头
对于队列来说,一种入队顺序,只有一种出队顺序
就比如说这张排队买火车票的示例来说,最先排队的人最先买到票,买到票也就可以直接提桶跑路了,也就不需要继续等待了,后面的人要想买到票只能等待前面的人买完了才能轮到他自己,否则的话是要一直等待下去的。有的小伙伴看到这里就会想,我可以插队啊!!在这里我只想说小伙子,你的思想很危险呐!路还长,大好青春可不能就此结束啊!!
所以队列也属于逻辑结构,是一种线性数据结构,它的特征当然是先进先出啦,队列的出口端叫作队头,队列的入口端叫作队尾
队列的实现
这里对于队列的实现我们使用链表的方式
结构体的创建:
typedef int QDataType;
typedef struct QueueNode
{
struct QueueNode* next;//指向下一个节点
QDataType data;//存储数据
}QueueNode;
typedef struct Queue
{
QueueNode* head;//头指针
QueueNode* tail;//尾指针
}Queue;初始化:
void QueueInit(Queue* pq)
{
assert(pq);
//把2个指针置空
pq->head = NULL;
pq->tail = NULL;
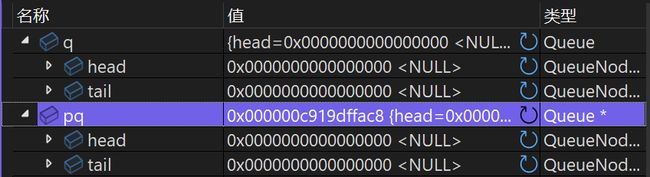
}注:初始化过后,各个参数对应的地址及指向
入队:
入队就是将新元素放入队列中,只允许在队尾的位置放入元素,新元素的下一个位置将会成为队尾
void QueuePush(Queue* pq, QDataType x)
{
assert(pq);
QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
newnode->data = x;
newnode->next = NULL;
//第一次插入
if (pq->head == NULL)//考虑队列为空的情况
{
pq->head = pq->tail = newnode;
}
//非第一次插入
else
{
//相当于链表的头插
pq->tail->next = newnode;//看解释1
//新节点变为新队尾
pq->tail = newnode;
}
}1️⃣pq->tail->next怎么理解?
pq->tail->next本质上是(pq->tail)->next,pq->tail是当前尾指针对应newnode,newnode的next就是新的尾节点
判空:
只需返回头结点是否为空,如果为空就是没有插入数据,可以以此来判断队列是否为空。
bool QueueEmpty(Queue* pq)
{
assert(pq);
//空链表返回true,非空链表返回false
return pq->head == NULL;
}出队:
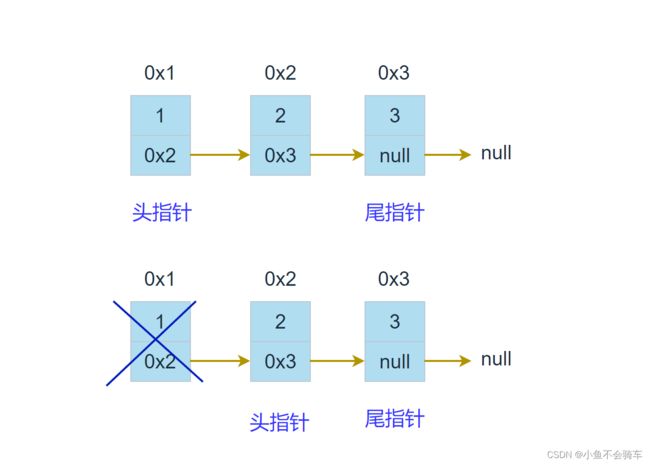
出队操作就是把元素移除队列,只允许在队头的一端移出元素,出队元素的后一个元素将会成为新的队头
不完善的写法:
void QueuePop(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));//如果是头和尾都是空了那么就是没有元素不用删了
QueueNode* next = pq->head->next;
free(pq->head);
pq->head = next;
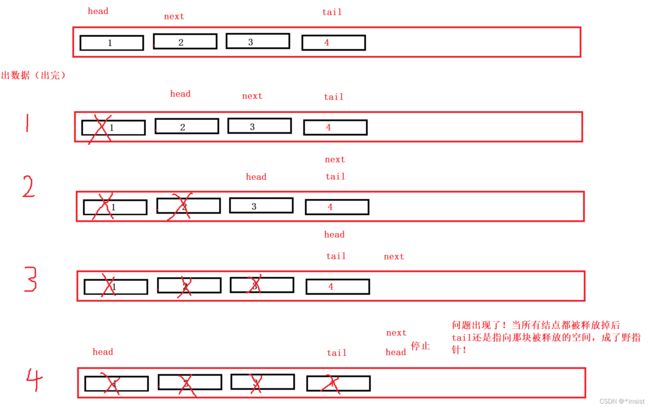
}问题所在:
完善的写法:(加一个判断条件)
void QueuePop(Queue* pq)
{
assert(pq);
//队列为空时不能删除
assert(!QueueEmpty(pq));
//只有一个节点的情况
if (pq->head->next == NULL)
{
free(pq->head);
pq->head = pq->tail = NULL;
}
//多个节点的情况
else
{
//相当于头删
QueueNode* next = pq->head->next;
free(pq->head) ;
pq->head = next;
}
}长度:
定义一个计数器size,遍历队列,只要结点不为空,size++,当为空结点是就结束,此时的count就是队列元素个数。
拓展:也可以在队列的结构中加一个size 即在Queue中再定义一个size,每次插入元素就size++,最后只需要返回Queue中的size即可,省去了遍历的步骤!
QDataType QueueSize(Queue* pq)
{
assert(pq);
//如果需要频繁的调用QueueSize这个接口,可以在Queue这个结构体中增加一个成员用于记录长度
int size = 0;
QueueNode* cur = pq->head;
while (cur)
{
size++;
cur = cur->next;
}
return size;
}取头:
因为我们保存了头尾指针,想要获取队头元素就直接返回头指针指向结点里的数据即可。
QDataType QueueFront(Queue* pq)
{
assert(pq);
//链表为空时不能取头
assert(!QueueEmpty(pq));
return pq->head->data;
}取尾:
因为我们保存了头尾指针,想要获取队尾元素就直接返回尾指针指向结点里的数据即可。
QDataType QueueBack(Queue* pq)
{
assert(pq);
//链表为空时不能取尾
assert(!QueueEmpty(pq));
return pq->tail->data;
}销毁:
void QueueDestory(Queue* pq)
{
assert(pq);
QueueNode* cur = pq->head;
//遍历链表
while (cur)//看解释1
{
//看解释2
QueueNode* next = cur->next;
free(cur);
cur = next;
}
//销毁完了就置空
pq->head = pq->tail = NULL;
}1️⃣
while(cur)等价于while(cur !=NULL)
不可以写成while(cur !=pq->tail),因为当cur==pq->tail时跳出循环,导致tail处的节点未被销毁
2️⃣为什么要先保存该节点的下一个节点的地址再释放该节点的空间?
如果我们一上来就把头节点的空间销毁了,那我们接下来怎么找下一个节点?靠头节点的next吗?不可能,头节点都销毁掉了,你再访问它就是非法访问了
完整代码:
这里需要三个文件
1️⃣ Queue.h,用于函数的声明
2️⃣ Queue.c,用于函数的定义
3️⃣ Test.c,用于测试函数
Queue.h
#pragma once
//头
#include
#include
#include
#include
//结构体
typedef int QDataType;
typedef struct QueueNode
{
struct QueueNode* next; //指向下一个节点
QDataType data; //存储整型数据
}QueueNode;
typedef struct Queue
{
QueueNode* head;//头指针
QueueNode* tail;//尾指针
}Queue;
//函数
void QueueInit(Queue* pq);
void QueuePush(Queue* pq, QDataType x);
bool QueueEmpty(Queue* pq);
void QueuePop(Queue* pq);
QDataType QueueSize(Queue* pq);
QDataType QueueFront(Queue* pq);
QDataType QueueBack(Queue* pq);
void QueueDestory(Queue* pq);
Queue.c
#include"Queue.h"
void QueueInit(Queue* pq)
{
assert(pq);
//把2个指针置空
pq->head = pq->tail = NULL;
}
void QueuePush(Queue* pq, QDataType x)
{
assert(pq);
//malloc空间,如果需要频繁的开辟空间建议再实现一个BuyQueueNode用于malloc
QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
if (newnode == NULL)
{
printf("malloc fail\n");
exit(-1);
}
newnode->data = x;
newnode->next = NULL;
//第一次插入
if (pq->head == NULL)
{
pq->head = pq->tail = newnode;
}
//非第一次插入
else
{
pq->tail->next = newnode;
pq->tail = newnode;
}
}
bool QueueEmpty(Queue* pq)
{
assert(pq);
//空链表返回true,非空链表返回false
return pq->head == NULL;
}
void QueuePop(Queue* pq)
{
assert(pq);
//链表为空时不能删除
assert(!QueueEmpty(pq));
//只有一个节点的情况
if (pq->head->next == NULL)
{
free(pq->head);
pq->head = pq->tail = NULL;
}
//多个节点的情况
else
{
QueueNode* next = pq->head->next;
free(pq->head) ;
pq->head = next;
}
}
QDataType QueueSize(Queue* pq)
{
assert(pq);
//如果需要频繁的调用QueueSize这个接口,可以在Queue这个结构体中增加一个成员用于记录长度
int sz = 0;
QueueNode* cur = pq->head;
while (cur)
{
sz++;
cur = cur->next;
}
return sz;
}
QDataType QueueFront(Queue* pq)
{
assert(pq);
//链表为空时不能取头
assert(!QueueEmpty(pq));
return pq->head->data;
}
QDataType QueueBack(Queue* pq)
{
assert(pq);
//链表为空时不能取尾
assert(!QueueEmpty(pq));
return pq->tail->data;
}
void QueueDestory(Queue* pq)
{
assert(pq);
QueueNode* cur = pq->head;
//遍历链表
while (cur)
{
QueueNode* next = cur->next;
free(cur);
cur = next;
}
pq->head = pq->tail = NULL;
}
Test.c
#include"Queue.h"
int main()
{
//1、传二级指针
//2、返回值
//3、带哨兵位的头节点
//4、嵌套结构体 (这里使用这种方式)
Queue q;
//初始化
QueueInit(&q);
//插入
QueuePush(&q, 1);
QueuePush(&q, 2);
QueuePush(&q, 3);
QueuePush(&q, 4);
//删除
QueuePop(&q);
QueuePop(&q);
//取头
QueueFront(&q);
//取尾
QueueBack(&q);
//释放
QueueDestory(&q);
return 0;
}
三、栈和队列面试题
有效的括号
题目描述:
思路:
这个题是一个类似于栈结构的问题,它需要在栈顶放入一个左括号,然后这时候有一个右括号和这个栈顶的左括号进行匹配,匹配完成后左括号出栈,如果失败则返回false,当所有括号都匹配完成以后,栈里面没有数据,这时候返回true
有几个点需要注意的点:
如果一开始就是右括号比如这种")(",那肯定是不匹配的,因此我们需要在读取第一个右括号时判断栈里面是否为空,如果为空则说明没有和这个右括号想匹配的左括号,这个时候返回false。
最终一定是栈里面没有数据才返回true,如果是这种情况{(),最终栈里面剩一个{,有数据,返回false。
代码实现:
typedef char STDataType;
typedef struct stack
{
STDataType* a;
int top;
int capacity;
}Stack;
//初始化
void stackInit(Stack* ps)
{
assert(ps);
ps->a = NULL;
ps->top = ps->capacity = 0;
}
//扩容
void checkCapacity(Stack* ps)
{
assert(ps);
if (ps->top == ps->capacity)
{
int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
STDataType* newA = (STDataType*)realloc(ps->a, sizeof(STDataType) * newCapacity);
if (newA == NULL)
{
printf("realloc fail");
exit(-1);//非正常运行导致退出程序
}
ps->capacity = newCapacity;
ps->a = newA;
}
}
//压栈
void stackPush(Stack* ps, STDataType x)
{
assert(ps);
checkCapacity(ps);
ps->a[ps->top] = x;
ps->top++;
}
//判空
bool stackEmpty(Stack* ps)
{
assert(ps);
return ps->top == 0;
}
//c出栈
void stackPop(Stack* ps)
{
assert(ps);
assert(!stackEmpty(ps));
ps->top--;
}
//栈顶
STDataType stackTop(Stack* ps)
{
assert(ps);
assert(!stackEmpty(ps));
return ps->a[ps->top - 1];
}
//销毁
void StackDestory(Stack* ps)
{
assert(ps);
free(ps->a);
ps->a = NULL;
ps->top = ps->capacity = 0;
}
bool isValid(char* s)
{
Stack st;
stackInit(&st);
//printf("%d\n",strlen(s));
//排除奇数字符串
if (strlen(s) % 2 != 0)
{
return false;
}
//偶数字符串进入
else
{
while (*s)//等价于*s!='\0','\0'对应的ASCLL码值和NULL一样是0
{
if (*s == '[' || *s == '(' || *s == '{')
{
stackPush(&st, *s);//入栈
++s;
//针对"["或"("或"{"这一情况
if (*s == NULL)
{
return false;
}
}
else
{
//针对"]"或"}"或")"这一情况
if (stackEmpty(&st))
{
return false;
}
STDataType top = stackTop(&st);
stackPop(&st);
if (
(*s == ')' && top != '(')
|| (*s == ']' && top != '[')
|| (*s == '}' && top != '{')
)
{
StackDestory(&st);
return false;
}
else
{
s++;
}
}
}
//针对"[[[]"这种跳出循环后还剩"[["栈不为空这种情况
if (!stackEmpty(&st))
{
return false;
}
return true;
}
}用队列实现栈
题目描述:
思路一
思路二
用栈实现队列
设计循环队列
题目描述:
思路一
思路二
四、概念选择题
1、一个栈的初始状态为空。现将元素1、2、3、4、5、A、B、C、D、E依次入栈,然后再依次出栈,则元素出栈的顺序是 ( )
A. 12345ABCDE
B. EDCBA54321
C. ABCDE12345
D. 54321EDCBA
解析:B,根据栈的特点 —— 后进先出,先进后出,可以得到正确答案
2、若进栈的序列为1,2,3,4,进栈过程中可以出栈,则下列不可能的一个出栈序列是 ( )
A. 1,4,3,2
B. 2,3,4,1
C. 3,1,4,2
D. 3,4,2,1
解析:C,本题需要注意的是进栈过程中可以出栈,这也导致了多种情况的出现:
进栈顺序:1 2 3 4
出栈顺序:1 2 3 4
4 3 2 1
… …
3、循环队列的存储空间为 Q(1:100) ,初始状态为 front=rear=100 。经过一系列正常的入队与退队操作后, front=rear=99 ,则循环队列中的元素个数为( )
A. 1
B. 2
C. 99
D. 0
解析:D,当循环队列进行一系列操作后,front == rear 说明为空;front == rear+1 说明为满
4、以下( )不是队列的基本运算?
A. 从队尾插入一个新元素
B. 从队列中删除第i个元素
C. 判断一个队列是否为空
D. 读取队头元素的值
解析:B,从队列的特性先进先出,后进后出即可知道答案
5、现有一循环队列,其队头指针为front,队尾指针为rear;循环队列长度为N,实际最多存储 N - 1 个数据。其队内有效长度为?( )
A. (rear - front + N) % N + 1
B. (rear - front + N) % N
C. (ear - front) % (N + 1)
D. (rear - front + N) % (N - 1)
解析:B,
这里分为两种情况:
1️⃣ 队列的有效长度是 (rear - front + N) % N == 3
对于第 1 种情况来说只需要 rear - front 即可,为什么还需要 +N 再 % N ❓❔
因为这里还有第 2 种情况,而仅仅是 rear - front 这个公式是不能满足第 2 种情况的
2️⃣ 队列的有效长度是 (rear - front + N) % N == 4
对于第 2 种情况来说只需要 rear + N - front 即可,为什么还需要 +N 再 % N ❓❔
因为本题是只有 1 个正确答案,所以还要顾虑到第 1 种情况,需要寻找能同时适用于两种情况的 1 个公式