以8位并行数据为例确定crc-32的一般矩阵表示形式

在进行数据校验时我们会使用到crc（循环冗余校验）校验的方式，例如在以太网通信网络中会对信息进行编码和校验，生成码采用的就是33位的

crc-32：x32+x26+x23+...+x2+x+1; (104c11db7)。循环冗余校验码的计算是模2的除法运算。模2指的是运算的时候不进行借位和进位的操作。可以用下面的例子来说明。假如信息码为11011，生成码为101（2+1）则校验码的计算过程是

先把信息码左移两位（二进制），得1101100。

然后通过异或操作

1101100

101

---------

 111100

 101

---------

 010100

  101

--------

  00000

这个计算结果为00

假如信信息码为1100时，余码就是01

110000

101

----

010000

 101

--------

 00100

   101

------

   001

所以根据上面的运算可以得出任何信息码的余码。

一般使用线性反馈移位寄存器LFSR或(LFSR2)来进行物理实现。这两种方式结构如下：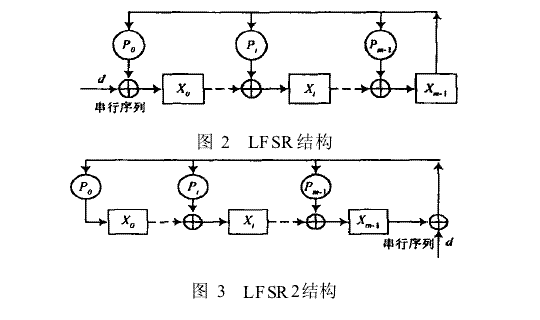

本篇文章我使用的是LFSR2结构，假如使用LFSR结构需要在先输入n位的0（n是冗余码的位数）。为简单起见推导过程使用的4位信息码，8位的冗余码，生成式为P={p7,p6,p5,p4,p3,p2,p1,p0},初始余码为X0={x0(7),x0(6),x0(5),x0(4),x0(3),x0(2),x0(1),x0(0)}。输入数据D={d3,d2,d1,d0}；

则当输入一位d3时表达式；+表示异或

x1(7)=x0(6)+p7(x0(7)+d3)=p7x0(7)+x0(6)+p7d3;

x1(6)=x0(5)+p6(x0(7)+d3)=p6x0(7)+x0(5)+p6d3;

x1(5)=x0(4)+p5(x0(7)+d3)=p5x0(7)+x0(4)+p5d3;

x1(4)=x0(3)+p4(x0(7)+d3)=p4x0(7)+x0(3)+p4d3;

x1(3)=x0(2)+p3(x0(7)+d3)=p3x0(7)+x0(2)+p3d3;

x1(2)=x0(1)+p2(x0(7)+d3)=p2x0(7)+x0(1)+p2d3;

x1(1)=x0(0)+p1(x0(7)+d3)=p1x0(7)+x0(0)+p1d3;

x1(0)=p0(x0(7)+d3)=p0x0(7)+p0d3;

X1'=FX0'+P'd3;其中

F={　p7,1,0,0,0,0,0,0

     p6,0,1,0,0,0,0,0

 　　p5,0,0,1,0,0,0,0

 　　p4,0,0,0,1,0,0,0    

 　　p3,0,0,0,0,1,0,0

 　　p2,0,0,0,0,0,1,0

　　 p1,0,0,0,0,0,0,1

 　　p0,0,0,0,0,0,0,0}

同样可以得X2'=FX1'+P'd2;

          X3'=FX2'+P'd1;

　　　　　X4'=FX3'+P'd0;

进而得X4'=F*F*F*F*X0+{F*F*F*P',F*F*P',F*P',P'}*D';

所以输入四位数据时最后余码的状态与初始的状态有关。

对于任意的n位并行信息码Xn=Fn*X0+{F(n-1)p'.....p'}D'。

下面是用表格对8位信息码，32位余码，生成码为0x04c11db7;

参考Excel表格。最后的结果为（左边为低位x0~x31）

以下为在verilog中的验证代码：

  1 module arc_8(input clk,output reg [31:0] crc);
  2 reg [4:0]count=0;
  3 reg [31:0] fcs_temp,datatemp2;
  4 reg [31:0] R ;
  5 reg[2:0] step=0;
  6 reg [7:0]data_count=0;
  7 reg [2:0] num=0;
  8 reg on=1;
  9 reg [7:0] datatemp;
 10 always@(posedge clk)
 11 begin 
 12         case(step)
 13             0:begin if(on) step<=1;else step<=0;R<=0;end 
 14             1:begin         
 15                                             if(data_count<126)begin // 主要是第一个循环0x60e84e34,验证的结果应该为0x7db9cbc8
 16                                             case(num)
 17                                                 0:begin datatemp<=8'h60;num<=1;on<=1;end
 18                                                 1:begin datatemp <=8'he8;num<=2;end
 19                                                 2:begin datatemp<=8'h4e;num<=3;end 
 20                                                 3:begin datatemp<=8'h34;num<=0;data_count<=data_count+1;end 
 21                                         endcase 
 22                                         step<=3;end
 23                                     else begin on<=0; step<=6;end end
 24             3:begin     step<=4;
 25                             //00100000100000000000000000000000
 26                             fcs_temp[31]<=R[23]^R[29];
 27                             //10010000010000000000000000000000
 28                             fcs_temp[30]<=R[22]^ R[28]^R[31];
 29                             //11001000001000000000000000000000
 30                             fcs_temp[29]<=R[21]^ R[27]^R[30]^R[31];
 31                             //01100100000100000000000000000000
 32                             fcs_temp[28]<=R[20]^R[26]^R[29]^R[30];
 33                             //10110010000010000000000000000000
 34                             fcs_temp[27]<=R[19]^R[25]^R[28]^R[29]^R[31];
 35                           //01011001000001000000000000000000
 36                           fcs_temp[26]<= R[18]^R[24]^R[27]^ R[28]^ R[30];
 37                             //00001100000000100000000000000000
 38                             fcs_temp[25]<=R[17]^R[26]^R[27];
 39                             //10000110000000010000000000000000
 40                             fcs_temp[24]<=R[16]^R[25]^R[26]^R[31];
 41                             //01000011000000001000000000000000
 42                             fcs_temp[23]<=R[15]^R[24]^R[25]^R[30];
 43                             //00000001000000000100000000000000
 44                             fcs_temp[22]<=R[14]^R[24];
 45                             //00100000000000000010000000000000
 46                             fcs_temp[21]<=R[13]^R[29];
 47                             //00010000000000000001000000000000
 48                             fcs_temp[20]<=R[12]^ R[28];
 49                             //10001000000000000000100000000000
 50                             fcs_temp[19]<=R[11]^R[27]^ R[31];
 51                             //11000100000000000000010000000000
 52                             fcs_temp[18]<=R[10]^ R[26]^R[30]^R[31];
 53                             //01100010000000000000001000000000
 54                             fcs_temp[17]<=R[ 9]^R[25]^R[29]^R[30];
 55                             //00110001000000000000000100000000
 56                             fcs_temp[16]<=R[ 8]^R[24]^R[28]^R[29];
 57                             //10111000000000000000000010000000
 58                             fcs_temp[15]<=R[ 7]^R[27]^R[28]^R[29]^R[31];
 59                             //11011100000000000000000001000000
 60                             fcs_temp[14]<=R[ 6]^R[26]^R[27]^R[28]^R[30]^R[31];
 61                             //11101110000000000000000000100000
 62                             fcs_temp[13]<=R[ 5]^R[25]^R[26]^R[27]^ R[29]^ R[30]^ R[31];
 63                             //01110111000000000000000000010000
 64                             fcs_temp[12]<=R[ 4]^R[24]^R[25]^R[26]^R[28]^R[29]^R[30];
 65                             //00011011000000000000000000001000
 66                             fcs_temp[11]<=R[ 3]^R[24]^R[25]^R[27]^R[28];
 67                             //00101101000000000000000000000100
 68                             fcs_temp[10]<=R[ 2]^R[24]^R[26]^R[27]^R[29];
 69                             //00110110000000000000000000000010
 70                             fcs_temp[9]<=R[ 1]^R[25]^R[26]^R[28]^R[29];
 71                             //00011011000000000000000000000001
 72                             fcs_temp[8]<=R[ 0]^R[24]^R[25]^R[27]^R[28];
 73                             //10101101000000000000000000000000
 74                             fcs_temp[7]<=R[24]^R[26]^R[27]^R[29]^R[31];
 75                             //11110110000000000000000000000000
 76                             fcs_temp[6]<=R[25]^R[26]^R[28]^R[29]^R[30]^R[31];
 77                             //11111011000000000000000000000000
 78                             fcs_temp[5]<=R[24]^R[25]^R[27]^R[28]^R[29]^R[30]^R[31];
 79                             //01011101000000000000000000000000
 80                             fcs_temp[4]<=R[24]^R[26]^R[27]^R[28]^R[30];
 81                             //10001110000000000000000000000000
 82                             fcs_temp[3]<=R[25]^R[26]^R[27]^R[31];
 83                             //11000111000000000000000000000000
 84                             fcs_temp[2]<=R[24]^R[25]^R[26]^R[30]^R[31];
 85                             //11000011000000000000000000000000
 86                             fcs_temp[1]<=R[24]^R[25]^R[30]^R[31];
 87                             //01000001000000000000000000000000
 88                             fcs_temp[0]<=R[24]^R[30];end
 89     
 90             4:begin     step<=5;
 91                                 datatemp2[31]<=datatemp[ 5];
 92                                 datatemp2[30]<=datatemp[ 4]^datatemp[ 7];
 93                                 datatemp2[29]<=datatemp[ 3]^datatemp[ 6]^datatemp[ 7];
 94                                 datatemp2[28]<=datatemp[ 2]^datatemp[ 5]^datatemp[ 6];
 95                                 datatemp2[27]<=datatemp[ 1]^datatemp[ 4]^datatemp[ 5]^datatemp[ 7];
 96                                 datatemp2[26]<=datatemp[ 0]^datatemp[ 3]^datatemp[ 4]^datatemp[ 6];
 97                                 datatemp2[25]<=datatemp[ 2]^datatemp[ 3];
 98                                 datatemp2[24]<=datatemp[ 1]^datatemp[ 2]^datatemp[ 7];
 99                                 datatemp2[23]<=datatemp[ 0]^datatemp[ 1]^datatemp[ 6];
100                                 datatemp2[22]<=datatemp[ 0];
101                                 datatemp2[21]<=datatemp[ 5];
102                                 datatemp2[20]<=datatemp[ 4];
103                                 datatemp2[19]<=datatemp[ 3]^datatemp[ 7];
104                                 datatemp2[18]<=datatemp[ 2]^datatemp[ 6]^datatemp[ 7];
105                                 datatemp2[17]<=datatemp[ 1]^datatemp[ 5]^datatemp[ 6];
106                                 datatemp2[16]<=datatemp[ 0]^datatemp[ 4]^datatemp[ 5];
107                                 datatemp2[15]<=datatemp[ 3]^datatemp[ 4]^datatemp[ 5]^datatemp[ 7];
108                                 datatemp2[14]<=datatemp[ 2]^datatemp[ 3]^datatemp[ 4]^datatemp[ 6]^datatemp[ 7];
109                                 datatemp2[13]<=datatemp[ 1]^datatemp[ 2]^datatemp[ 3]^datatemp[ 5]^datatemp[ 6]^datatemp[ 7];
110                                 datatemp2[12]<=datatemp[ 0]^datatemp[ 1]^datatemp[ 2]^datatemp[ 4]^datatemp[ 5]^datatemp[ 6];
111                                 datatemp2[11]<=datatemp[ 0]^datatemp[ 1]^datatemp[ 3]^datatemp[ 4];
112                                 datatemp2[10]<=datatemp[ 0]^datatemp[ 2]^datatemp[ 3]^datatemp[ 5];
113                                 datatemp2[9]<=datatemp[ 1]^datatemp[ 2]^datatemp[ 4]^datatemp[ 5];
114                                 datatemp2[8]<=datatemp[ 0]^datatemp[ 1]^datatemp[ 3]^datatemp[ 4];
115                                 datatemp2[7]<=datatemp[ 0]^datatemp[ 2]^datatemp[ 3]^datatemp[ 5]^datatemp[ 7];
116                                 datatemp2[6]<=datatemp[ 1]^datatemp[ 2]^datatemp[ 4]^datatemp[ 5]^datatemp[ 6]^datatemp[ 7];
117                                 datatemp2[5]<=datatemp[ 0]^datatemp[ 1]^datatemp[ 3]^datatemp[ 4]^datatemp[ 5]^datatemp[ 6]^datatemp[ 7];
118                                 datatemp2[4]<=datatemp[ 0]^datatemp[ 2]^datatemp[ 3]^datatemp[ 4]^datatemp[ 6];
119                                 datatemp2[3]<=datatemp[ 1]^datatemp[ 2]^datatemp[ 3]^datatemp[ 7];
120                                 datatemp2[2]<=datatemp[ 0]^datatemp[ 1]^datatemp[ 2]^datatemp[ 6]^datatemp[ 7];
121                                 datatemp2[1]<=datatemp[ 0]^datatemp[ 1]^datatemp[ 6]^datatemp[ 7];
122                                 datatemp2[0]<=datatemp[ 0]^datatemp[ 6];end 
123     
124              5:begin R<=fcs_temp^datatemp2; step<=1;end             
125             6:begin step<=0;crc<=~R;end 
126             endcase
127 end
128 endmodule

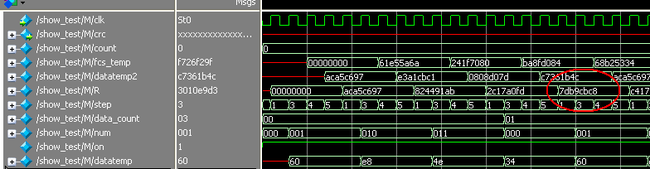
modelsim 中显示结果