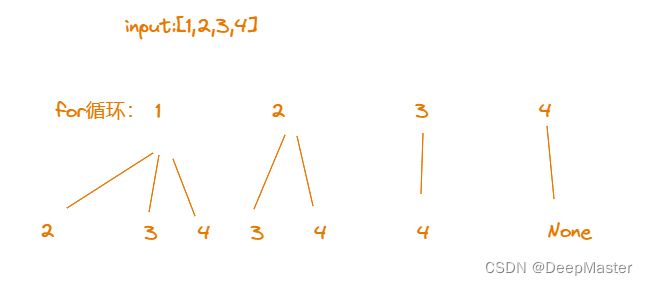代码随想录算法训练营第二十四天|77. 组合
Leetcode - 77
首先,回溯,回溯是隐藏在递归中的一个现象,就是递归向上传递的操作。
有些问题,比如列举的问题,使用for循环可能要嵌套无数多层,无法解决。此处只能用回溯算法来解决这种问题。 是一种暴力的方式,效率不高。
回溯算法适用于五种问题:
1. 组合问题: 比如一个序列中,求指定长度的所有组合,注意,组合是不讲究顺序的,[1,2]和[2,1]是同一个。
2. 切割问题: 比如一个字符串按照某种切分方式,使得切分出来的子串都是回文串。
3, 子集问题:穷举一个序列所有的子序列。
4. 排列问题:求N个数按照一定规则全排列的所有排列方式,注意排列是有顺序的, [1,2]和[2,1]是有区别的。
5.棋盘问题: N皇后,数独。
解题的模版就是
终止条件 + 处理逻辑 , for循环 : for循环内部是处理逻辑 + 递归 + 回溯。
回到这题,参数,这里n,k都是定死的值,不会随着递归而改变,这里我不将其作为递归的参数。
res可以作为全局变量,参数暂时想到用一个列表temp来装临时的值。
终止条件: temp的长度为k,则将temp中的内容加入结果集res,注意此处不能直接append temp,否则在temp进行改变的时候,res中已经存入的结果也会随之改变,可以deepcopy一份再append,也可以直接append(temp[:])。
for循环: 从某个值开始,然后到n结束,这里我们想到我们开始的值是会变化的,比如1,2... 所以每次递归的时候我们需要传入一个开始的值,所以这里参数列表加一个curr,代表当前起始值。
循环内部,temp append当前循环值,
递归: 传入temp,注意此处要传入i+1,让下一次递归是从当前起始值后一个位置开始。
回溯: 每次向上传递时,回退一个值,即temp进行一次pop
def combine(self, n: int, k: int) -> List[List[int]]:
res = []
def makeCombination(temp, curr):
nonlocal res
if len(temp) == k:
res.append(temp[:])
return
# 这里可以设想,第一次进入for循环,i的值是1,递归下次传入的curr是i+1,也就是后一个值,依次类推,1会与2,3...n一一进行匹配,1为起点结束后,不断回溯,此时i变为2,递归传入i+1,也就是3,2再与其后面的元素3,4,...n进行匹配。这样就是整个穷举的过程
for i in range(curr, k+1):
temp.append(i)
makeCombination(temp, i+1)
temp.pop()
makeCombination([], 1)
return res如图,for循环里第一行数就是我们代码设定的for循环,底下的分支,对应的就是递归的过程,通过不断递归产生如下分支。
再如图 ,n=4,k=4, 只有1 2 3 4一条路径是符合要求的,其余的路径比如[1,2],在[1,2,3]已经被选择的情况下,只能再选择4,但是4已经是最后一个元素了,就算加入4,长度也满足不了k,所以这条路径是不用遍历的,包括后面的路径也是一个道理,这里我们就可以进行剪枝,让不可能满足条件的路径不用再去花费功夫去递归了
可以看到 第一层for循环里,到2之后就可以判断递归不用再继续了,因为后序的元素无法满足要求,所以在第一层for循环时就要加条件予以限制。
假设当前序列集长度为t, 所以此时还需要 k-t个元素进行填充。 所以下一次for循环的起始值,也就是下一个元素的值最少要等于 (k+1) - t (注:这里可以带值进行测算,如t = 2,k = 4,k-t = 2,若从2开始肯定是没有限制的,因为序列中已有两个元素了,所以此时一下个元素至少要从3开始,此时就是 k - t +1),python for循环中是左闭右开的形式,所以要想让右边取到 k- t +1这个值,需要再加1,也就是 (k+1) - t +1
def combine(self, n: int, k: int) -> List[List[int]]:
res = []
def makeCombination(temp, curr):
nonlocal res
if len(temp) == k:
res.append(temp[:])
return
last = n +1 - (k- len(temp))
# 这里相当于是做了一次筛选,若curr的值大于last,则说明不应该再继续下去。对于range,step设为默认值的情况下,start若大于end,则不会再继续循环
for i in range(curr, last + 1):
temp.append(i)
makeCombination(temp, i+1)
temp.pop()
makeCombination([], 1)
return res因为是条件限制的关系,所以也可以写成下面形式
def combine(self, n: int, k: int) -> List[List[int]]:
res = []
def makeCombination(temp, curr):
nonlocal res
if len(temp) == k:
res.append(temp[:])
return
last = n +1 - (k- len(temp))
#此处是将在for循环中进行的判断提前了
if curr > last:
return
for i in range(curr, n + 1):
temp.append(i)
makeCombination(temp, i+1)
temp.pop()
makeCombination([], 1)
return res