计算能力足够强大，所有加密算法原理上都会被破解吗

转载自：http://blog.sina.com.cn/s/blog_185c43eee0102ypk1.html

苏盛辉  2018-06-29

 

1  引言

    2018年5月28日，潘建伟教授在两院院士大会上做了一个科普性质的报告：新量子革命助力中国成为信息技术引领者[1]。其中提到：“一旦拥有足够强大的计算能力，所有依赖于计算复杂度的加密算法原理上都会被破解”。对此，我们实在不敢苟同。

    注意，在标题中，我们省略了定语“依赖于计算复杂度的”，但下面的讨论不会省略它。

 

2  什么是计算复杂度

    计算复杂度(Computational Complexity，也叫计算复杂性)与问题及解决问题的算法有关。简单地讲，计算复杂度就是在某种计算模型上解决问题的困难程度[2][3]。

    一个问题如果在确定型图灵机上存在多项式时间算法，就是易解的，否则就是难解的。

    例如，给一亿个正整数按大小排列顺序(即排序问题)，就是易解的问题。再例如，给一所大学按某些条件排定课表(排课问题)，就是难解的问题，尤其，当该大学拥有一千个班时，即使使用超级计算机来排定一个最佳的课表也需要上百年时间。又例如，因式分解问题、离散对数问题等也是难解的问题[4][5]。

    在确定型图灵机上有多项式时间解(算法)的问题叫P问题(P是一个类，包含所有的P问题)，在非确定型图灵机上有多项式时间解的问题叫NP问题(NP也是一个类，包含所有的NP问题)[5][6]。P是否等于NP是计算复杂性理论的中心问题，也是美国Clay数学研究所悬赏100万美金求解的千禧年问题之一(图1)[7]。目前，人们普遍倾向于相信有P ≠ NP。

 

图1:  P ≠ NP或P = NP证明的悬赏

 

    按照广义Church-Turing命题(其并没有被证明却被许多人相信)，在确定型图灵机上还没有被找到多项式时间算法的因式分解问题和离散对数问题，其在电子计算机上的多项式时间算法也同样不会被找到。

    然而，人们在量子图灵机(也叫通用量子计算机，简称量子计算机，是实际量子计算机的样板)这种新的计算模型上发现了因式分解问题、离散对数问题的多项式时间求解算法(得益于量子比特的叠加和纠缠)[8][9]，这对广义Church-Turing命题提出了严重挑战[3]。不过，这并不意味着在量子计算机上所有问题都存在多项式时间求解算法了。

 

3  计算复杂度与绝对安全悖论

    从文献[2][3][4]知，凡是企图用计算机来解决或求解的问题都涉及到计算复杂度。

 

3.1  绝对安全悖论的产生

    潘建伟教授在2016年6月接受记者采访时表示：世界上第一封绝对不会被截、被破、被复制(即绝对安全)的密信将要诞生。传统的加密手段，都是依赖所谓的计算复杂度。但是随着计算能力的增加，在某种程度上肯定是会被破解的。而量子通信利用基于物理学的基本原理，利用微光世界的最小单元，在原理上将实现不会被破解的奇迹[10]。

    正如我们在2018年6月18日所指出，这些话在内涵上是相互矛盾的，从而导致了绝对安全悖论[11]。

    首先，量子通信(或量子保密通信)是一种混合通信，它有两个信道：一个量子信道和一个经典信道。量子信道用于协商和发送密钥，本身并不做加密和解密操作，经典信道用于加密、传输密文和解密。在追求一次一钥完美安全情况下，加密和解密通过异或运算完成。

    其次，利用穷举搜索从密文寻找明文(它是一段有意义的文字)是一个典型的与计算复杂度相关的问题[2][3]，其时间复杂度一般为2 ^ n步骤，这里n为密文的比特长度。这表明量子通信也依赖于计算复杂度。

    最后，量子计算机的计算能力是足够强大的，按照潘教授的话，在量子计算机上所有与密码相关的问题都会被破解(即都存在多项式时间算法)，那么，穷举搜索明文问题也存在多项式时间算法，这样，量子通信也就不安全了。因而，绝对安全的悖论就产生了。

    注意，利用Grover量子搜索算法，人们能在2 ^ (n / 2)步骤内以较大概率找到明文[12]，不过，这仍然是指数时间量级，而非多项式时间量级。

 

3.2  没有任何原理表明在量子计算机上所有依赖于计算复杂度的密码算法都会被破解

    类似于图灵机上的易解或难解问题，一个问题如果在量子图灵机上存在有界错误多项式时间算法，就是易解的，否则就是难解的。

    同样地，BQP和QMA在量子图灵机上被定义[13][14]。BQP是BPP的量子相似体，而BPP可以被认为是P的概率版本；QMA是MA的量子相似体，而MA可以被认为是NP的概率版本。

    正如人们目前不能证明P ≠ NP或P = NP一样，人们目前亦不能证明BQP ≠ QMA或BQP = QMA，但事实让人们倾向于相信BQP ≠ QMA[13][14]。

    实际上，迄今为止，人们在量子计算机上只发现了因式分解问题、离散对数问题、椭圆离散对数问题的多项式时间算法[9]，它们属于隐含子群类问题。绝大多数NP难题(包括非隐含子群类问题)，例如多变量问题、格问题、非范子集积问题等，并没有被发现存在量子多项式时间算法。为什么被人们发现的求解NP问题的量子多项式时间算法会很少呢？Shor给出了解释：(1) 量子计算以一种不同于经典计算的方式进行运算，人们用于设计经典算法的技术以及对于经典计算的直觉不适用于量子计算；(2) 也许真的存在很少的问题, 对于这些问题的求解, 量子计算能够提供相对于经典计算的实质加速, 但大多数或者全部此类量子算法已经被发现[15]。

    因此，没有任何原理表明在量子计算机上依赖于计算复杂度的密码算法都会被破解。相反，相对安全证明理论和大量的事实表明在量子计算机上存在不会被破解的密码算法(体制)[16]，包括对称算法和非对称算法[17][18]。

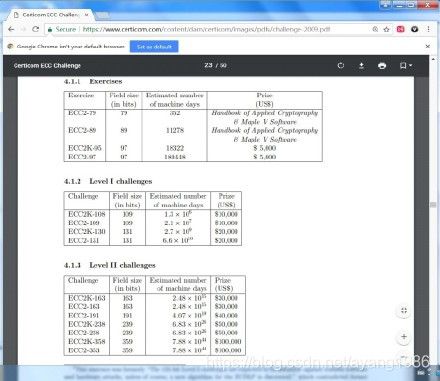
    密码的安全就像药物的安全一样，不可能从理论上证明其绝对安全，只能从临床实验上保证其足够安全。众所周知，人们(当然，包括潘建伟教授在内)不会因为药物的绝对安全性没有被证明就不使用药物了，密码也是这个道理。什么是密码的临床实验呢？那就是密码难题的公开悬赏破解，它是国际密码学界的一种通常做法。例如，RSA密码就如此做了[19]， ECC密码也如此做了(图2)[20]。 

图2:  ECC的破解悬赏

 

    ECC破解悬赏目前仍是有效的，具体要求和说明请见文献[20]。

 

4  实质上密码算法的安全性主要是与计算模型有关 而与计算能力无太大关系

    在电子计算机时代，密码算法(无论是对称算法还是非对称算法)为什么能够生存，这是因为加密和解密操作是可以在多项式时间内完成的，而破译(即破解)却不能在多项式时间内完成，只能在亚指数或指数时间内完成，即解密和破译之间存在时间复杂度的量级差。

    为什么基于因式分解问题的RSA密码算法在“神威”和“天河”等超级计算机上仍然是安全的(即不可破解的)呢？这是因为“神威”和“天河”仍然属于电子计算机的范畴，因式分解问题是难题的论断在其上并没有被改变。不错，“神威”和“天河”的速度和内存是很大，计算能力是很强，但是，只需线性地提高RSA的安全参数(即模数的比特长度)就可以抵消这种速度和内存带来的威胁，这就是具体安全，一种水涨船高的安全。例如，在“神威”或“天河”超级计算机上，1024比特的RSA不再具体安全了，但2048或4096比特的RSA仍是具体安全的。当然，随着安全参数的提升，RSA的加密与解密效率会大大降低，这也是RSA正逐渐退出历史舞台、被ECC取代的原因。

    量子计算机是一种新的计算模型。在该模型上，解决因式分解问题的新型算法被设计，导致因式分解问题是难题的论断被改变，RSA解密和破译之间的时间复杂度量级差不再存在，这样，即使4096或8192比特的RSA也无济于事了。另一方面，对于多变量问题、格问题、非范子集积问题等而言，它们在量子计算机上仍是难题(这意味着即使运用量子计算机，至少也要在亚指数或指数时间内才能求解它们)，这样，基于它们的密码算法仍然存在解密和破译之间的时间复杂度量级差，因而，此类密码在量子计算机上仍然是安全的，这就是后量子密码。对后量子密码理论和技术的研究就是后量子密码学[21][22]。

    因此，密码算法的安全性实质上主要是与计算模型有关，而与计算能力无太大关系。

 

5  结束语

    我们建议，专家们在做科普时，一定要深入理解相关学科的核心知识，了解国际上相关技术的现状，从而尽量做到深入浅出、以小见大、一分为二、实事求是。当然，我们不会认为，一些专家为了夸大某种技术和贬低另一种技术而故意混淆是非或扭曲一些国际上已达成的共识。

    量子密码与后量子密码到底孰优孰劣，除了国内技术探讨之外，还一定要看国际上主要国家的趋势，尤其为现代密码学的奠基和发展做出了重要贡献的国家的趋势。

    在信息技术领域，为达成既定目标选择做某事或不做某事、选择走某路线或不走某路线，性价比是一个极其重要的考虑因素。不做不等于落后。当然，自己有钱自己做，没人能管，但花国家的钱、花老百姓的钱来做就是另外一码事了。

 

参考文献

[1] 高雅丽. 潘建伟院士: 新量子革命助力中国成为信息技术引领者. 中国科学报, 2018年5月31日.

[2] W. Dean. Computational Complexity Theory. Stanford Encyclopedia of Philosophy, Stanford University, Jul 2016.

[3] D. Z. Du and K. Ko. Theory of Computational Complexity. John Wiley & Sons, New York, 2000.

[4] M. Sipser. Introduction to the Theory of Computation. PWS Publishing, Boston, 1997.

[5] A. Menezes, P. Oorschot, and S. Vanstone. Handbook of Applied Cryptography. CRC Press, London, UK, 1997.

[6] B. Schneier. Applied Cryptography: Protocols, Algorithms, and Source code in C (2nd Edition). John Wiley & Sons, New York, 1996.

[7] Clay Mathematics Institute. Millennium Problems. http://www.claymath.org/millennium-problems, May 2000.

[8] D. Deutsch. Quantum Theory, the Church-Turing Principle and the Universal Quantum Computer. Proceedings of the Royal Society A. 400(1818), Jul 1985, pp: 97–117.

[9] P. W. Shor. Polynomial-time Quantum Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM Journal on Computing, v26(5), 1997, pp: 1484 - 1509.

[10] 桂楷东. 潘建伟: 专用量子计算机有望十年内面世. 中国科技网, 2016年6月6日.

[11] 苏盛辉. 这三个悖论 愿与潘建伟教授探讨. http://blog.sina.com.cn/s/blog_185c43eee0102yocm.html, 2018年6月18日.

[12] L. K. Grover. A Fast Quantum Mechanical Algorithm for Database Search. Proc. of STOC '96, Pennsylvania, May 22 - 24, 1996, pp: 212-219.

[13] D. Aharonov and T. Navehy. Quantum NP - A Survey. https://arxiv.org/pdf/quant-ph/0210077.pdf, Oct 2002.

[14] J. Watrous. Quantum Computational Complexity. Encyclopedia of Complexity and Systems Science, v1-10, 2009, pp: 7174–7201.

[15] P. W. Shor. Why Haven't More Quantum Algorithms Been Found. Journal of the ACM, v50(1), 2003, pp: 87 - 90.

[16] S. Su, S. Lü, X. Fan. Asymptotic Granularity Reduction and Its Application. Theoretical Computer Science, v412(39), 2011, pp: 5374-5386.

[17] National Institute of Standards and Techno (NIST). Report on Post-Quantum Cryptography (NISTIR 8105). http://csrc.nist.gov/publications/drafts/nistir-8105/nistir_8105_draft.pdf, Feb 03, 2016.

[18] National Cyber Security Centre UK. Quantum Key Distribution. https://www.ncsc.gov.uk/, Oct 04, 2016.

[19] RSA Challenge Administrator. Announcement of RSA Factoring Challenge. RSA Data Security, Mar 18, 1991.

[20] CR. Certicom ECC Challenge. https://www.certicom.com/content/dam/certicom/images/pdfs/challenge-2009.pdf, Nov 6, 1997 (revised Nov 10, 2009).

[21] D. J. Bernstein, J. Buchmann, and E. Dahmen. Post-Quantum Cryptography. Springer, 2009.

[22] Dustin Moody. Post-Quantum Cryptography: NIST's Plan for the Future. National Institute of Standards and Technology (NIST), 2016.