4. Python--Scipy库（上/1-6）

本文非常全面的介绍了Scipy库，希望大家有耐心的看下去。参考链接在最后。

目录：

1. Scipy简介

    1.1 子包

    1.2 数据结构

2. Scipy开发环境安装

    2.1 Windows

    2.2 Linux

3. Scipy基本功能

    3.1 内在Numpy数组创建

    3.2 矩阵

4. Scipy簇聚

    4.1 Scipy中实现K-Means

    4.2 三个集群计算K均值

5. Scipy常量

    5.1 Scipy常量包

    5.2 可用常量列表

6. FFTpack

    6.1 快速傅立叶变换

    6.2 离散余弦变换

7. 积分

8. 插值

9. 输入/输出

10. Linalg

11. Ndimage

12. 优化算法

13. 统计函数

14. CSGraph

15. Scipy空间

16. Scipy ODR

17. Scipy特殊包

------------------------------------------------------------------------------

1. Scipy简介

SciPy，发音为Sigh Pi，是一个科学的python开源代码，在BSD许可下分发的库，用于执行数学，科学和工程计算。

SciPy库依赖于NumPy，它提供了便捷且快速的N维数组操作。 SciPy库的构建与NumPy数组一起工作，并提供了许多用户友好和高效的数字实践，例如:数值积分和优化的例程。 它们一起运行在所有流行的操作系统上，安装快速且免费。 NumPy和SciPy易于使用，但强大到足以依靠世界上一些顶尖的科学家和工程师。

1.1 SciPy子包

SciPy被组织成覆盖不同科学计算领域的子包。 这些总结在下表中 -

scipy.cluster   矢量量化/Kmeans（https://docs.scipy.org/doc/scipy/reference/cluster.html#module-scipy.cluster，，，，以下同此）

scipy.constants   物理和数学常数

scipy.fftpack   傅里叶变换

scipy.integrate   集成例程

scipy.interpolate   插值

scipy.io   数据输入和输出

scipy.linalg   线性代数例程

scipy.ndimagen   维图像包

scipy.odr   正交距离回归

scipy.optimize   优化

scipy.signal   信号处理

scipy.sparse   稀疏矩阵

scipy.spatial   空间数据结构和算法

scipy.special   任何特殊的数学函数

scipy.stats   统计

 

1.2 数据结构

SciPy使用的基本数据结构是由NumPy模块提供的多维数组。 NumPy为线性代数，傅立叶变换和随机数生成提供了一些功能，但与SciPy中等效函数的一般性不同。

 

2. Scipy开发环境安装

标准Python发行版不捆绑任何SciPy模块。 一个轻量级的选择是使用流行的Python包安装程序安装SciPy，

$ pip install pandas

如果安装Anaconda Python软件包，默认情况下会安装Pandas。 以下是将它们安装在不同操作系统中的软件包和链接。

2.1 Windows

Anaconda(来自https://www.continuum.io)是SciPy堆栈的免费Python发行版。 它也适用于Linux和Mac。有关安装的教程请参考:https://www.yiibai.com/pandas/python_pandas_environment_setup.html

Canopy(https://www.enthought.com/products/canopy/)免费提供，以及用于Windows，Linux和Mac的完整SciPy堆栈的商业发行。

Python(x，y)- 这是一个免费的Python发行版，其中包含用于Windows操作系统的SciPy堆栈和Spyder IDE。 (可从https://python-xy.github.io/下载)

 

2.2 Linux

各个Linux发行版的软件包管理器用于在SciPy堆栈中安装一个或多个软件包。

Ubuntu

可以使用以下路径在Ubuntu中安装Python。

$ sudo apt-get install python-numpy python-scipy

python-matplotlibipythonipython-notebook python-pandas python-sympy python-nose

Shell

Fedora

可以使用以下路径在Fedora中安装Python。

sudo yum install numpyscipy python-matplotlibipython python-pandas

sympy python-nose atlas-devel

 

3. Scipy基本功能

默认情况下，所有的NumPy函数都可以通过SciPy命名空间获得。 当导入SciPy时，不需要显式导入NumPy函数。 NumPy的主要目标是均匀多维数组。 它是一个元素表(通常是数字)，都是相同类型，由正整数的元组索引。 在NumPy中，大小(尺寸)被称为轴。 轴的数量称为等级。

现在，让修改NumPy中的Vectors和Matrices的基本功能。 由于SciPy构建在NumPy数组之上，因此需要了解NumPy基础知识。 由于线性代数的大多数部分只处理矩阵。

NumPy向量

向量(Vector)可以通过多种方式创建。 其中一些描述如下。

将Python数组类对象转换为NumPy中的数组，看看下面的例子。

import numpy as np

list=[1,2,3,4]

arr=np.array(list)

print(arr)

执行上面示例代码，得到以下结果 -

[1 2 3 4]

 

3.1 内在NumPy数组创建

NumPy有从头开始创建数组的内置函数。 其中一些函数解释如下。

使用zeros()

zeros(shape)函数将创建一个用指定形状(shape)填充0值的数组。 默认dtype是float64。 看看下面的例子。

import numpy as np

print(np.zeros((2,3)))

执行上面示例代码，得到以下结果 -

array([[ 0., 0., 0.],

[ 0., 0., 0.]])

 

使用ones()

ones(shape)函数将创建一个填充1值的数组。 它在所有其他方面与0相同。 看看下面的例子。

import numpy as np

print(np.ones((2,3)))

执行上面示例代码，得到以下结果 -

array([[ 1., 1., 1.],

[ 1., 1., 1.]])

使用arange()

arange()函数将创建具有有规律递增值的数组。 看看下面的例子。

import numpy as np

print(np.arange(7))

执行上面示例代码，得到以下结果 -

array([0, 1, 2, 3, 4, 5, 6])

 

定义值的数据类型

看看下面一段示例代码 -

import numpy as np

arr=np.arange(2,10,dtype=np.float)

print(arr)

print("Array Data Type :",arr.dtype)

执行上面示例代码，得到以下结果 -

[ 2. 3. 4. 5. 6. 7. 8. 9.]

Array Data Type : float64

 

使用linspace()

linspace()函数将创建具有指定数量元素的数组，这些元素将在指定的开始值和结束值之间平均间隔。 看看下面的例子。

import numpy as np

print(np.linspace(1.,4.,6))

执行上面示例代码，得到以下结果 -

array([ 1. , 1.6, 2.2, 2.8, 3.4, 4. ])

 

3.2 矩阵

矩阵是一个专门的二维数组，通过操作保留其2-D特性。 它有一些特殊的运算符，如*(矩阵乘法)和**(矩阵幂值)。 看看下面的例子。

import numpy as np

print(np.matrix('1 2; 3 4'))

执行上面示例代码，得到以下结果 -

matrix([[1, 2],

[3, 4]])

矩阵的共轭转置

此功能返回自我的(复数)共轭转置。 看看下面的例子。

import numpy as np

mat=np.matrix('1 2; 3 4')

print(mat.H)

执行上面示例代码，得到以下结果 -

matrix([[1, 3],

        [2, 4]])

 

矩阵的转置

此功能返回自身的转置。看看下面的例子。

import numpy as np

mat=np.matrix('1 2; 3 4')

print(mat.T)

执行上面示例代码，得到以下结果 -

matrix([[1, 3],

        [2, 4]])

 

当转置一个矩阵时，我们创建一个新的矩阵，其行是原始的列。 另一方面，共轭转置为每个矩阵元素交换行和列索引。 矩阵的逆矩阵是一个矩阵，如果与原始矩阵相乘，则产生一个单位矩阵。

 

4. Scipy簇聚

K均值聚类是一种在一组未标记数据中查找聚类和聚类中心的方法。 直觉上，我们可以将一个群集(簇聚)看作 - 包含一组数据点，其点间距离与群集外点的距离相比较小。 给定一个K中心的初始集合，K均值算法重复以下两个步骤 -

对于每个中心，比其他中心更接近它的训练点的子集(其聚类)被识别出来。

计算每个聚类中数据点的每个要素的平均值，并且此平均向量将成为该聚类的新中心。

重复这两个步骤，直到中心不再移动或分配不再改变。 然后，可以将新点x分配给最接近的原型的群集。 SciPy库通过集群包提供了K-Means算法的良好实现。 下面来了解如何使用它。

4.1 SciPy中实现K-Means

我们来看看并理解如何在SciPy中实现K-Means。

导入K-Means

下面来看看每个导入的函数的实现和用法。

from SciPy.cluster.vq import kmeans,vq,whiten

 

数据生成

我们需要生成(模拟)一些数据来探索聚类。参考以下代码 -

from numpy import vstack,array

from numpy.random impor trand

# data generation with three features 

data=vstack((rand(100,3)+array([.5,.5,.5]),rand(100,3)))

现在，我们来看看生成的模拟数据，上述程序将生成以下输出。

[[ 1.34103331  1.13924682  0.68465819]

[ 1.28481332  0.91318917  0.84225546]

[ 0.96498008  1.42382266  0.83564809]

[ 1.37049373  0.66635033  1.46568707]

[ 0.87424166  0.86090225  1.22545336]

[ 1.0264795  0.90724604  1.46837972]

[ 1.40996857  1.37769991  1.39805802]

[ 0.964556    0.71632157  1.47983347]

[ 0.69909637  1.21695335  1.46434369]

[ 1.01887602  0.86448455  1.02242951]

[ 0.82573176  1.19165063  1.09085707]

[ 0.64378227  0.70673944  0.69484097]

[ 1.16087103  0.64371977  0.89720984]

[ 1.23410673  0.56805382  1.33534058]

[ 0.50417695  1.29632466  0.96589447]

[ 0.91395183  1.39173555  1.0748435 ]

[ 1.04540644  1.20721464  0.97173727]

... ...

[ 0.79250839  0.48689797  0.42250824]

[ 0.05846914  0.83469742  0.57586067]

[ 0.0308333  0.8642561  0.1111777 ]

[ 0.61327069  0.43425013  0.99716439]

[ 0.81698148  0.91098877  0.12706862]

[ 0.60665992  0.55999208  0.57454962]

[ 0.13894142  0.03315365  0.43182983]

[ 0.62293781  0.34701877  0.61229591]]

根据每个要素标准化一组观察值。 在运行K-Means之前，使用白化重新缩放观察集的每个特征维度是有好处的。 每个特征除以所有观测值的标准偏差以给出其单位差异。

美化数据

我们可使用以下代码来美白数据。

# whitening of data

data=whiten(data)

print(data)

 

4.2 用三个集群计算K均值

现在使用以下代码计算三个群集的K均值。

# computing K-Means with K = 3 (2 clusters)

centroids,_=kmeans(data,3)

上述代码对形成K个簇的一组观测向量执行K均值。 K-Means算法调整质心直到不能获得足够的进展，即失真的变化，因为最后一次迭代小于某个阈值。 在这里，可以通过使用下面给出的代码打印centroids变量来观察簇。

print(centroids)

上面的代码将生成以下输出。

print(centroids)[[2.260347021.439243351.3697022][2.637885722.814464622.85163854][0.735072561.308018551.44477558]]

使用下面给出的代码将每个值分配给一个集群。

# assign each sample to a cluster

clx,_=vq(data,centroids)

vq函数将'M'中的每个观察向量与'N'obs数组与centroids进行比较，并将观察值分配给最近的聚类。 它返回每个观察和失真的聚类。 我们也可以检查失真。使用下面的代码检查每个观察的聚类。

# check clusters of observation

print(clx)

上面的代码将生成以下输出。

array([1,1,0,1,1,1,0,1,0,0,1,1,1,0,0,1,1,0,0,1,0,2,0,2,0,1,1,1,0,0,1,1,0,0,1,1,0,0,0,0,1,1,0,0,1,1,0,0,1,0,1,0,0,0,1,1,0,0,0,1,0,1,0,0,1,0,0,0,0,0,0,0,0,0,1,0,0,1,0,0,1,0,0,0,0,0,0,0,0,1,0,0,0,0,1,0,0,1,2,1,2,2,2,2,2,2,2,2,0,2,0,2,2,2,2,2,0,0,2,2,2,1,0,2,0,2,2,2,2,2,2,2,2,2,0,2,2,1,2,2,2,2,2,2,2,2,2,2,2,2,0,2,0,2,2,2,2,2,2,2,2,2,0,2,2,2,2,0,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2],dtype=int32)

Python

上述数组的不同值 0,1,2表示簇。

 

5. Scipy常量

SciPy常量(constant)包提供了广泛的常量，用于一般科学领域。

5.1 SciPy常量包

scipy.constants包提供了各种常量。必须导入所需的常量并根据需要来使用它们。下面看看这些常量变量是如何导入和使用的。

首先，通过下面的例子来比较'pi'值。

#Import pi constant from both the packages

import scipy

import math

print("sciPy - pi = %.16f"%scipy.constants.pi)

print("math - pi = %.16f"%math.pi)

执行上面示例代码，得到以下结果 -

sciPy - pi = 3.1415926535897931

math - pi = 3.1415926535897931

 

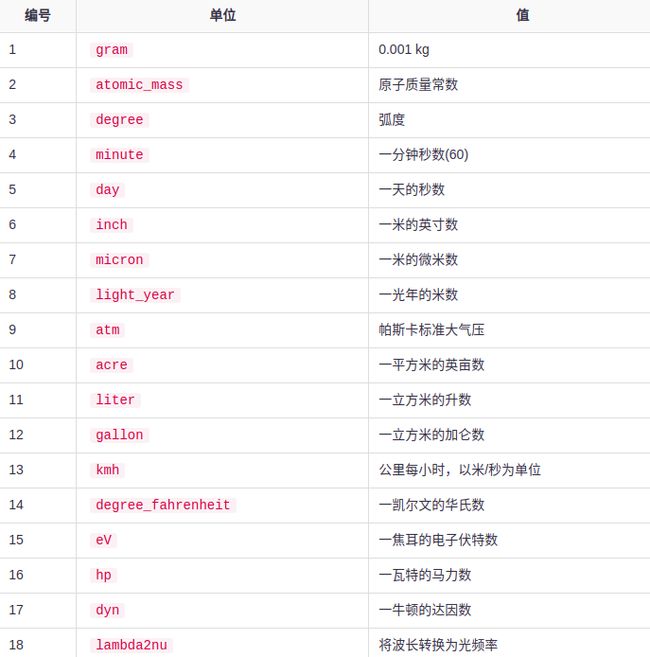
5.2 可用的常量列表

下表简要介绍了各种常数(常量)。

数学常量

物理常量

下表列出了最常用的物理常量。

单位

下表列出了SI单位。

这些单位范围从yotta，zetta，exa，peta，tera ...... kilo，hector，... nano，pico，...到zepto。

其他重要常量

下表列出了SciPy中使用的其他重要常量。

要记住所有这些都有点困难。可使用scipy.constants.find()方法获取指定键的简单方法。 看看下面的例子。

import scipy.constants

res=scipy.constants.physical_constants["alpha particle mass"]

print(res)

执行上面示例代码，得到以下结果 -

(6.64465723e-27, 'kg', 8.2e-35)

 

6. Scipy FFTpack

对时域信号计算傅里叶变换以检查其在频域中的行为。 傅里叶变换可用于信号和噪声处理，图像处理，音频信号处理等领域。SciPy提供fftpack模块，可让用户计算快速傅立叶变换。

以下是一个正弦函数的例子，它将用于使用fftpack模块计算傅里叶变换。

6.1 快速傅立叶变换

下面来了解一下快速傅立叶变换的细节。

一维离散傅立叶变换

长度为N的序列x [n]的FFT y [k]由fft()计算，逆变换使用ifft()计算。 看看下面的例子

#Importing the fft and inverse fft functions from fftpackage

from scipy.fftpack import fft

 

#create an array with random n numbers

x=np.array([1.0,2.0,1.0,-1.0,1.5])

 

#Applying the fft function

y=fft(x)

print(y)

执行上面示例代码，得到以下结果 -

[ 4.50000000+0.j          2.08155948-1.65109876j  -1.83155948+1.60822041j

-1.83155948-1.60822041j  2.08155948+1.65109876j]

 

再看另一个示例 -

#Importing the fft and inverse fft functions from fftpackage from scipy.fftpack import fft

from scipy.fftpack import ifft

#create an array with random n numbers

x=np.array([1.0,2.0,1.0,-1.0,1.5])

#Applying the fft function

y=fft(x)

#FFT is already in the workspace, using the same workspace to for inverse transform

yinv=ifft(y)

print(yinv)

执行上面示例代码，得到以下结果 -

[ 1.0+0.j  2.0+0.j  1.0+0.j -1.0+0.j  1.5+0.j]

 

scipy.fftpack模块允许计算快速傅立叶变换。 作为一个例子，一个(嘈杂的)输入信号可能看起来如下 -

import numpy as np 

time_step=0.02

period=5

time_vec=np.arange(0,20,time_step)

sig=np.sin(2*np.pi/period*time_vec)+0.5*np.random.randn(time_vec.size)

print(sig.size)

我们正以0.02秒的时间步长创建一个信号。 最后一条语句显示信号sig的大小。 输出结果如下 -

1000

 

我们不知道信号频率; 只知道信号sig的采样时间步长。 信号应该来自实际函数，所以傅里叶变换将是对称的。scipy.fftpack.fftfreq()函数将生成采样频率，scipy.fftpack.fft()将计算快速傅里叶变换。

下面通过一个例子来理解这一点。

from scipy import fftpack

sample_freq=fftpack.fftfreq(sig.size,d=time_step)

sig_fft=fftpack.fft(sig)

print(sig_fft)

执行上面示例代码，得到以下结果 -

array([

  25.45122234 +0.00000000e+00j,  6.29800973 +2.20269471e+00j,

  11.52137858 -2.00515732e+01j,  1.08111300 +1.35488579e+01j,

  …….])

 

6.2 离散余弦变换

离散余弦变换(DCT)根据以不同频率振荡的余弦函数的和表示有限数据点序列。 SciPy提供了一个带有函数idct的DCT和一个带有函数idct的相应IDCT。看看下面的一个例子。

from scipy.fftpack import dct

mydict=dct(np.array([4.,3.,5.,10.,5.,3.]))

print(mydict)

执行上面示例代码，得到以下结果 -

[ 60.          -3.48476592   -13.85640646    11.3137085    6.          -6.31319305]

 

逆离散余弦变换从其离散余弦变换(DCT)系数重建序列。idct函数是dct函数的反函数。 可通过下面的例子来理解这一点。

from scipy.fftpack import dct 

from scipy.fftpack importi dct

d=idct(np.array([4.,3.,5.,10.,5.,3.]))

print(d)

执行上面示例代码，得到以下结果 -

[ 39.15085889 -20.14213562  -6.45392043  7.13341236  8.14213562

 

参考：https://docs.python.org/3/

https://www.yiibai.com/scipy/scipy_introduction.html