【C++】哈夫曼树模拟实现

一. 什么是哈夫曼树

1. 基本术语介绍

在解释什么是哈夫曼树之前，先介绍三个基本术语：节点的路径长度、节点的权重和树的带权路径长度。

节点的路径长度

当前节点到根节点路径中边的个数称为该节点的路径长度。

节点的权值

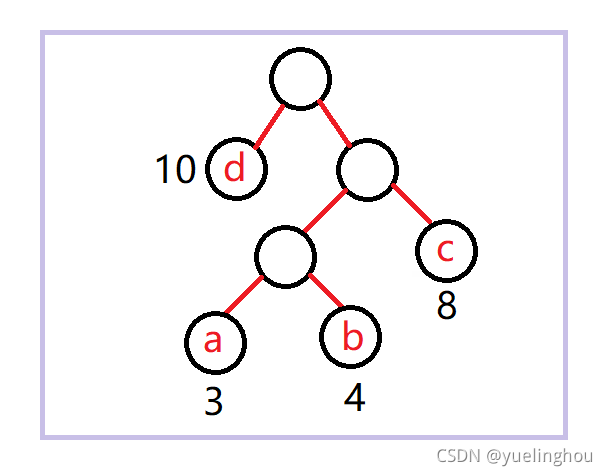
权重就是重要程度，权重越大表示越重要。在哈夫曼树中每个节点都存有自己的权重。比如说从一段文本中统计出a、b、c、d四个字母出现的次数分别为3、4、8、10，说a结点的权值为3，意思是说a结点在系统中占有3这个份量。实际上也可以化为百分比来表示，但反而麻烦,实际上是一样的。

struct HuffmanNode 
{
  // 数据域 
  int _weight;// 权值
  char _data; // 存储的数据
  // 指针域
  int _parent;
  int _left;
  int _right;
};

树的带权路径长度

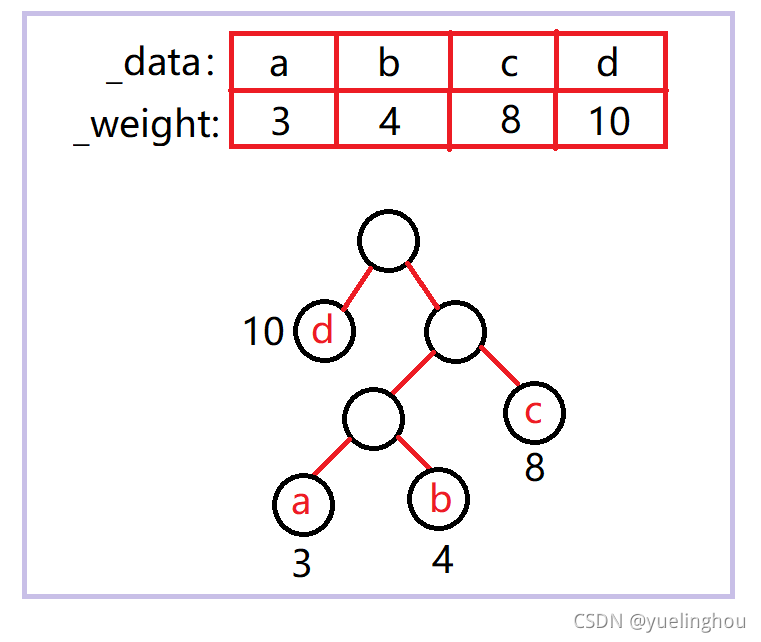
各个叶子节点的路径长度乘上它们的权值，最后累加得到的值称为这棵树的带权路径长度。

下图给出了每个叶子节点的权重，计算这棵树的带权路径长度等于：3 * 3 + 4 * 3 + 8 * 2 + 10 * 1 = 47。

2. 哈夫曼树的概念

接下来给出哈夫曼树的定义：哈夫曼树就是带权路径长度最短的二叉树，也叫作最优二叉树。

3. 哈夫曼树的特点

在哈夫曼树中我们只关心叶子节点，每个叶子节点的。给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树。

特点一：权值较大的结点离根较近

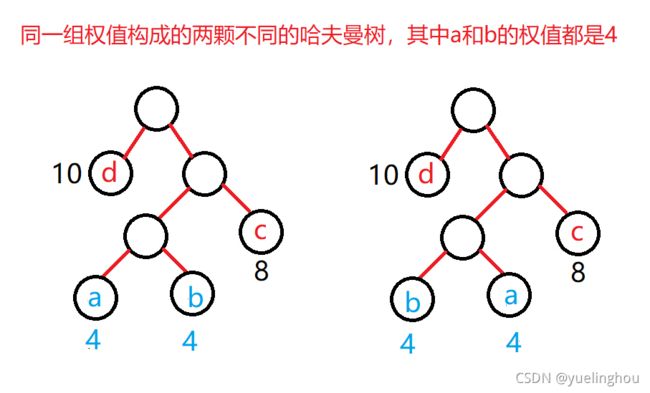
特点二：同一组权值构造出来的哈夫曼树不唯一

因为没有限定左右子树，并且有权值重复时，可能树的高度都不唯一，唯一的只是带权路径长度之和最小。

---

二. 为什么要有哈夫曼树

1. 表示哈夫曼编码

哈夫曼树的存在是为了表示哈夫曼编码的，什么是哈夫曼编码呢？该编码方法完全依据字符出现概率来构造异字头的平均长度最短的密码，有时称之为最佳编码，一般就叫做Huffman编码。

编码原则是左子树标0，右子树标1，结合这个原则看看不同权重的字符编码后的结果。

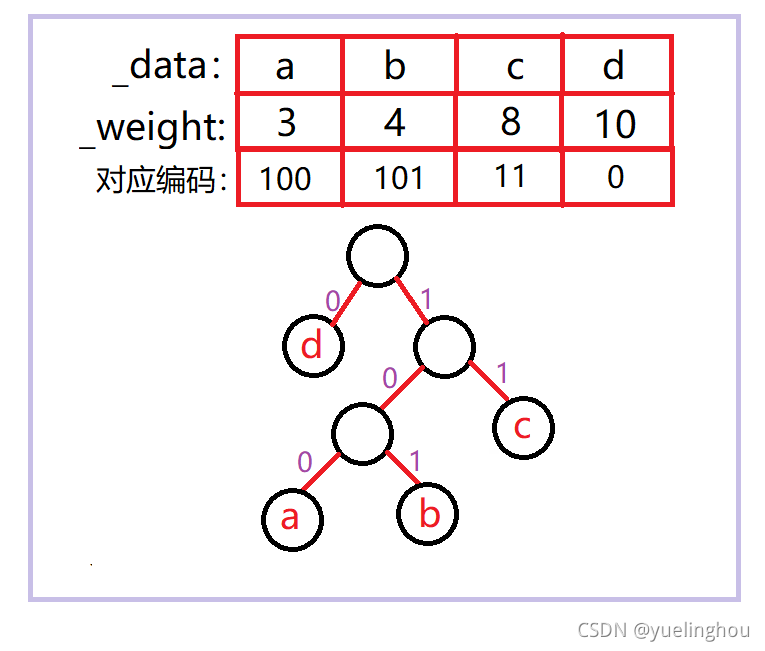
可以发现权重越大的节点所对应的编码长度越短，这是由哈夫曼树特点所决定的，因为在哈夫曼树中权值较大的结点离根较近。

2. 哈夫曼编码的特点

在哈夫曼编码的定义中可以看到这种编码方式有两个特点：各个字符对应的编码是异字头和编码的平均长度最短。可以推测既然哈夫曼编码是基于哈夫曼树表示的，那么这种编码方式的特点一定与哈夫曼树的特点强关联。

特点一：各个字符的编码是异字头的

解释这句话就是，一个字符的编码肯定不是另一个字符的前缀。因为在哈夫曼树中字符所对应的节点都是叶子节点（具体怎么实现会在后面的构造哈夫曼树中讲到），叶子节点之间是不会存在祖宗和子孙之间的关系的。

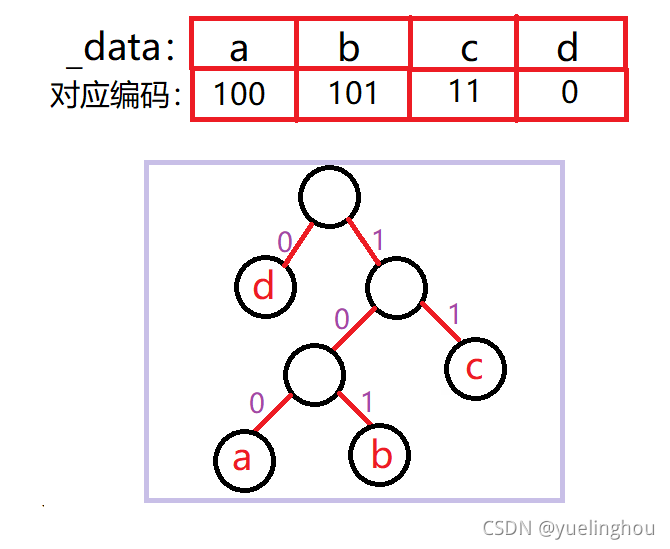
特点二：编码的平均长度最短

假如在我们要编码的机密文本中统计出a、b、c、d四个字符出现的次数分别为3、4、8、10。这个时候如果把这些字符单纯按照ASCLL码所对应数字的二进制表示编码的话就如下图这样：

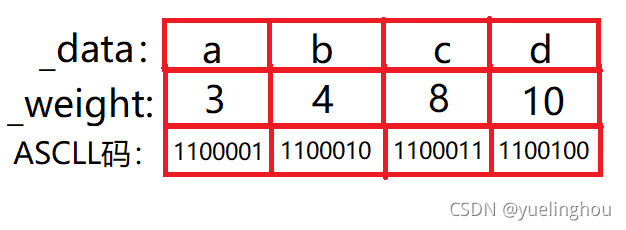
直接采用ASCLL码值来编码的方式会有一个弊端：这里完全不考虑字符出现的频率，每个字符对应的编码长度都是7位数字，这样在译码时虽然可以明确每7位数字就是一个字符，但是会导致最终整个编码后的文本的长度过长。

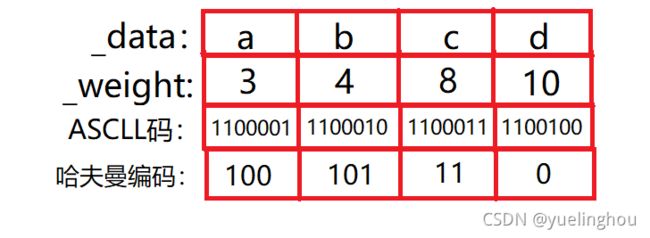
而采用哈夫曼编码的话就可以同时解决上面的两个问题：各个字符的编码是异字头这个已经说过了。对应哈夫曼树而言权重越大（出现频率越高）的字符越靠近根节点，根据编码规则得到的对应编码长度相对更短，这样就能达到整个文本编码后的的平均长度最短。

---

三. 哈夫曼树的构造、编码、译码实现

1. 场景说明

构造哈夫曼树

开始我们给定N个权值及其对应的字符作为哈夫曼树的N个叶子结点，哈夫曼树的构造原则是每次选两个权值最小的节点构造一个局部哈夫曼树，其中最小的节点为左孩子，次小的为右孩子，如果选取的两个节点权值相等，则取排在前一个位置的为左孩子。

1. 假设给定4个字符及其对应的权值：a(3)、b(4)、c(8)、d(10)。选两棵根结点权值最小的哈夫曼树作为左、右子树，构造一棵新的局部哈夫曼树，且置局部哈夫曼树根结点的权值为其左、右子树上根节点权值之和。
   
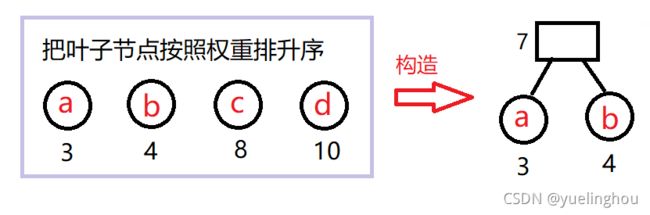
2. 用新的局部哈夫曼树替换掉原来的那两颗树，然后重复上一步操作：按权重排序、构造局部哈夫曼树。直到最终才剩一颗树了，这棵树就是最终的哈夫曼树。
   

对叶子节点进行编码和译码

编码：输入一个字符串，利用已建立好的哈夫曼树对字符串进行编码。

译码：输入一个二进制数字串，利用已建立的哈夫曼树将数字串进行译码。

2. 哈夫曼树基本框架

声明两个类：哈夫曼树本体和节点类。

哈夫曼树本体框架

构造时我们传入n个字符及其对应的权值，n个字符代表n个叶子节点，根据二叉树的性质可以算出总的节点个数为：2*n - 1。既然节点个数是定死的，为了达到随机访问的效果，我们采用数组来存储每个节点的指针。

使用哈希表存储字符到对应编码的映射键值对和编码到对应字符的键值对，这样在编码和译码过程中可以高效查询。

其中哈夫曼树的构造、编码和译码操作都是封装在哈夫曼树本体里完成的。

// 霍夫曼树本体的声明
class HuffmanTree 
{
      typedef HuffmanNode Node;
  private:
	  int _num;// 记录有效节点个数
	  vector<Node*> _t;// 顺序数组存储霍夫曼树节点
	  unordered_map<char, string> _makeCodeList;// 编码列表
	  unordered_map<string, char> _translateCodeList;// 译码列表
};

节点类基本框架

节点为三叉链结构，存有指向其左孩子、右孩子和父亲的下标，此外还有该节点所存储的字符和权值。

// 节点的声明
struct HuffmanNode 
{
  // 节点的构造函数
  HuffmanNode()
    :_weight(-1)
    ,_parent(0)
    ,_left(0)
    ,_right(0)
    ,_data(0)
  {}
  // 节点的拷贝构造函数
  HuffmanNode(const HuffmanNode& hnode)
  {
    _weight = hnode._weight;
    _parent = hnode._parent;
    _left = hnode._left;
    _right = hnode._right;
    _data = hnode._data;
  }
  // 数据域
  int _weight;
  char _data;
  // 指针域
  int _parent;
  int _left;
  int _right;
};

3. 哈夫曼树的构造函数

在哈夫曼树的构造函数里主要完成两个工作，即处理好哈夫曼树本体里的几个成员变量：

• new出树的所有节点，把各个节点的地址放到成员变量_t中，并处理好每个节点的指针域和数据域的内容，形成一颗逻辑上的哈夫曼树。
• 根据传入的数据，算出各个字符所对应的编码并把这种映射关系补充到编码列表_makeCodeList和译码列表_translateCodeList中。

第一步：初始化哈夫曼树

我们传入n个字符及其对应的权值。 根据传入的数据完成所有节点的创建和处理好叶子节点的权重和数据。特别注意虽然有效节点个数是2n-1，但为了从下标1开始表示我们创建2n个节点，其中下标为0的节点是没有意义的，[1, n]是叶子节点，[n+1, 2n-1]是非叶子节点。

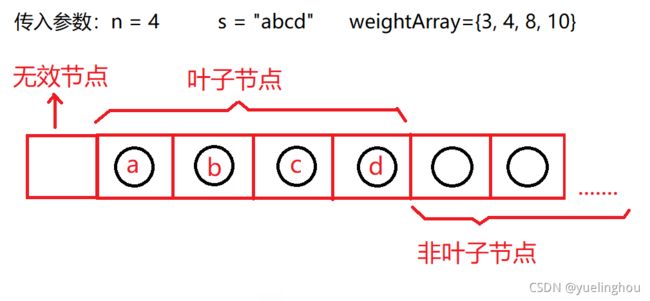
// n为叶子节点个数
// s为叶子对应的字符
// weightArray为叶子节点对应的权值
void InitHuffmanTree(int n, const string& s, const vector<int>& weightArray)
{
	// 1、创建出所有节点
	int m = 2 * n - 1;
	_num = m;
	_t.resize(m + 1);
	for (int i = 0; i <= m; ++i)
	{
		_t[i] = new HuffmanNode;
	}
	// 2、处理叶子节点的权重和数据
	for (int i = 1; i <= n; ++i)
	{
		_t[i]->_data = s[i - 1];
		_t[i]->_weight = weightArray[i - 1];
	}
}

第二步：构造哈夫曼树

处理非叶子节点的数据域和指针域，每一次都是构建一颗局部哈夫曼树，处理完最后一个非叶子节点时整颗哈夫曼树就算构造完成了。

// n为叶子节点个数
void CreateHuffmanTree(int n)
{
	// 遍历和处理所有非叶子节点
	for (int i = n + 1; i <= 2*n-1; ++i)
	{
		int s1 = 0;
		int s2 = 0;
		// Select作用是挑选[1, i-1]范围内按照权重排序的最小和次小的那两个节点s1和s2
		// 把找到的s1和s2作为下标为i的非叶子节点的左右孩子，构成一颗局部哈夫曼树
		Select(i, s1, s2);
		_t[i]->_left = s1;
		_t[i]->_right = s2;
		_t[i]->_weight = _t[s1]->_weight + _t[s2]->_weight;
		_t[s1]->_parent = i;
		_t[s2]->_parent = i;
	}
}

Select

Select()函数的作用为每次选择前1到i-1个结点，挑选两个双亲域为0且权值最小的节点，利用s1和s2返回两个结点的下标。
接着将两个节点的双亲域赋值为当前节点的下标i，将当前节点的孩子域分别置为s1和s2，最后将两个节点权值相加，储存在当前“生成”结点的weight。

// 因为_t类型是Node*
// 我们自己定义一个自己的比较方式：按照权重大小来比较
static bool cmp(Node* n1, Node* n2)
{
	return n1->_weight <= n2->_weight;
}
// 这里tmp我们开index个空间，拷贝原霍夫曼树中下标为[1, index]的节点到tmp中
// 拷贝完成后对tmp的每个节点依据权重排升序
void Select(int index, int& s1, int& s2)
{
	vector<Node*> tmp(index);
	for (int i = 0; i < index; ++i)
	{
		tmp[i] = new HuffmanNode(*_t[i + 1]);
	}
	sort(tmp.begin(), tmp.end(), cmp);
	// ret用来存储在tmp中排序后的权重最、次小且父亲为0的节点，在_t中对应的下标
	vector<int> ret(2, -1);
	int count = 0;
	// 从前往后遍历已经排好序的tmp，去找父亲为0的节点
	for (int i = 1; i < index; ++i)
	{
		if (tmp[i]->_parent == 0)
		{
			// 找到后，又到_t中寻找对应与该节点对应权值相同的，并且父母也为0的不重复的节点
			for (int j = 1; j < index; ++j)
			{
				if (_t[j]->_weight == tmp[i]->_weight && _t[j]->_parent == 0 && j != ret[0])
				{
					ret[count++] = j;
					break;
				}
			}
		}
		if (count == 2)
		{
			break;
		}
	}
	// 更新输出型参数
	s1 = ret[0];
	s2 = ret[1];
	// 最后释放tmp开辟的节点
	for (auto& e : tmp)
	{
		delete e;
	}
}

第三步：处理编码、译码列表

遍历每一个叶子节点，从下往上直到根节点，用一个字符串记录该叶子节点的编码，最后把字符串翻转后结合节点的数据放到编码、译码列表中。

// n为叶子节点个数
void HandleList(int n)
{
    // 遍历每一个叶子节点
    // 沿着路径往上直到根节点位置，翻转后得到该叶子节点的编码
    // 最后把该叶子节点的数据和对应的编码存放到哈希结构的编码、译码列表中
	for (int i = 1; i <= n; ++i)
	{
		string code;
		int cur = i;
		int parent = _t[cur]->_parent;
		while (parent)
		{
			if (_t[parent]->_left == cur)
			{
				code += '0';
			}
			else
			{
				code += '1';
			}
			cur = parent;
			parent = _t[cur]->_parent;
		}
		reverse(code.begin(), code.end());
		_makeCodeList.insert(make_pair(_t[i]->_data, code));
		_translateCodeList.insert(make_pair(code, _t[i]->_data));
	}
}

4. 编码

已经处理好编码列表之后，根据传入的字符串遍历里面的每一个字符，在哈希结构的编码表中搜索该字符对应的编码并输出，最终得到一连串二进制的编码结果。

// s为需要编码的文本
void MakeCode(const string& s)
{
	for (auto e : s)
	{
		cout << _makeCodeList.find(e)->second;
	}
	cout << endl;
}

5. 译码

因为各个字符对应的编码都是异字头的，所以我们译码时，从头到尾遍历一遍这些二进制编码，利用substr拿到子串到译码列表里搜索，找到后输出对应的字符，并从下一个位置继续拿出子串去搜索。

// s为需要翻译成文本的二进制编码序列
void TranslateCode(const string& s)
{
	size_t pos = 0;
	size_t first = 0;
	while (first < s.size())
	{
		++pos;
		auto it = _translateCodeList.find(s.substr(first, pos));
		if (it != _translateCodeList.end())
		{
			cout << it->second;
			first += pos;
			pos = 0;
		}
	}
	cout << endl;
}

---

四. 完整代码

【问题描述】

利用哈夫曼编码进行信息通信可以大大提高信道利用率，缩短信息传输时间，降低传输成本。但是，这要求在发送端通过一个编码系统对待传输数据预先编码，在接收端将传来的数据进行译码。对于双工信道，每端都需要一个完整的编码/译码系统。试为这样的信息收发站写一个哈夫曼的编/译码系统。

一个完整的系统具有以下几种操作：

• 0：初始化（Initialization）。从终端读入字符集大小n，以及n个字符和n个权值，建立哈夫曼树。

• 1：编码（Encoding）。输入一个字符串，利用已建立好的哈夫曼树对字符串进行编码，并输出编码后的结果。

• 2.译码（Decoding）。输入一个二进制数字串，利用已建立的哈夫曼树将数字串进行译码，并输出结果。

为了保证通信顺利进行，编码要求按统一规范进行，构造哈夫曼树的构造原则是每次选两个权值最小的节点构造一个新的哈夫曼树，其中最小的节点为左孩子，次小的为右孩子，如果选取的两个节点权值相等，则取排在前一个位置的为左孩子。编码原则是左子树标0，右子树标1。现给出操作序列，要求根据操作指令和输入数据，输出相应的结果。

【输入形式】

首先输入一个整数Q，表示操作的次数。

接下来输入Q行，每行表示一次操作，用整数X表示操作类型。

T=0时，输入一个整数n以及n个字符和n个权值，用空格分隔。

T=1时，输入一个待编码字符串。

T=2时，输入一个二进制字符串，表示已编码的字符串。

【输出形式】

当T=1时，输出一行编码结果

当T=2时，输出一行译码结果

【样例输入】

3

0 3 a b c 1 2 4

1 abcabc

2 0001100011

【样例输出】

0001100011

abcabc

【样例说明】

由于哈夫曼树的构造结果不唯一，注意题目要求中哈夫曼树的编码规范。

字符仅限大小写字母和数字，大小写敏感。

#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

// 节点的声明
struct HuffmanNode
{
	// 节点的构造函数
	HuffmanNode()
		:_weight(-1)
		, _parent(0)
		, _left(0)
		, _right(0)
		, _data(0)
	{}
	// 节点的拷贝构造函数
	HuffmanNode(const HuffmanNode& hnode)
	{
		_weight = hnode._weight;
		_parent = hnode._parent;
		_left = hnode._left;
		_right = hnode._right;
		_data = hnode._data;
	}

	// 节点的成员变量
	int _weight;
	int _parent;
	int _left;
	int _right;
	char _data;
};

// 霍夫曼树的声明
class HuffmanTree
{
	typedef HuffmanNode Node;
public:
	HuffmanTree()
	{}

	HuffmanTree(int n, const string& s, const vector<int>& weightArray)
	{
		// 1、初始化哈夫曼树
		InitHuffmanTree(n, s, weightArray);
		// 2、构造哈夫曼树
		CreateHuffmanTree(n);
		// 3、处理编码、译码列表
		HandleList(n);
	}

	// 编码
	void MakeCode(const string& s)
	{
		for (auto e : s)
		{
			cout << _makeCodeList.find(e)->second;
		}
		cout << endl;
	}

	// 译码
	void TranslateCode(const string& s)
	{
		size_t pos = 0;
		size_t first = 0;
		while (first < s.size())
		{
			++pos;
			auto it = _translateCodeList.find(s.substr(first, pos));
			if (it != _translateCodeList.end())
			{
				cout << it->second;
				first += pos;
				pos = 0;
			}
		}
		cout << endl;
	}

	// 析构函数释放空间
	// 释放我们构造时new出来的每一个节点
	~HuffmanTree()
	{
		for (auto e : _t)
		{
			delete e;
		}
	}

	// 霍夫曼树专属的swap，内部其实是调用的每个成员变量自己类型的swap
	void swap(HuffmanTree& ht)
	{
		_t.swap(ht._t);
		std::swap(_num, ht._num);
		_makeCodeList.swap(ht._makeCodeList);
		_translateCodeList.swap(ht._translateCodeList);
	}

private:
	// 哈夫曼树初始化
	void InitHuffmanTree(int n, const string& s, const vector<int>& weightArray)
	{
		// 1、创建所所有节点
		int m = 2 * n - 1;
		_num = m;
		_t.resize(m + 1);
		for (int i = 0; i <= m; ++i)
		{
			_t[i] = new HuffmanNode;
		}
		// 2、处理叶子节点的权重和数据
		for (int i = 1; i <= n; ++i)
		{
			_t[i]->_data = s[i - 1];
			_t[i]->_weight = weightArray[i - 1];
		}
	}

	// 构建哈夫曼树
	void CreateHuffmanTree(int n)
	{
		// 整合叶子节点和非叶子节点，使其成为一颗霍夫曼树
		for (int i = n + 1; i <= 2 * n - 1; ++i)// 遍历非叶子节点
		{
			int s1 = 0;
			int s2 = 0;
			// Select作用是挑选[1, i-1]范围内按照权重排序的最小和次小的那两个节点s1和s2
			// 当前i是还未处理的非叶子节点
			Select(i, s1, s2);
			// 把找到的s1和s2作为下标为i的非叶子节点的左右孩子，构成一颗局部哈夫曼树
			_t[i]->_left = s1;
			_t[i]->_right = s2;
			_t[i]->_weight = _t[s1]->_weight + _t[s2]->_weight;
			_t[s1]->_parent = i;
			_t[s2]->_parent = i;
		}
	}

	// 因为_t类型是Node*
	// 我们自己定义一个自己的比较方式：按照权重大小来比较
	static bool cmp(Node* n1, Node* n2)
	{
		return n1->_weight <= n2->_weight;
	}
	// 这里tmp我们开index个空间，拷贝原霍夫曼树中下标为[1, index]的节点到tmp中
	// 拷贝完成后对tmp的每个节点依据权重排升序
	void Select(int index, int& s1, int& s2)
	{
		vector<Node*> tmp(index);
		for (int i = 0; i < index; ++i)
		{
			tmp[i] = new HuffmanNode(*_t[i + 1]);
		}
		sort(tmp.begin(), tmp.end(), cmp);
		// ret用来存储在tmp中排序后的权重最、次小且父亲为0的节点，在_t中对应的下标
		vector<int> ret(2, -1);
		int count = 0;
		// 从前往后遍历已经排好序的tmp，去找父亲为0的节点
		for (int i = 1; i < index; ++i)
		{
			if (tmp[i]->_parent == 0)
			{
				// 找到后，又到_t中寻找对应与该节点对应权值相同的，并且父母也为0的不重复的节点
				for (int j = 1; j < index; ++j)
				{
					if (_t[j]->_weight == tmp[i]->_weight && _t[j]->_parent == 0 && j != ret[0])
					{
						ret[count++] = j;
						break;
					}
				}
			}
			if (count == 2)
			{
				break;
			}
		}
		// 更新输出型参数
		s1 = ret[0];
		s2 = ret[1];
		// 最后释放tmp开辟的节点
		for (auto& e : tmp)
		{
			delete e;
		}
	}

	// 处理编码、译码列表
	void HandleList(int n)
	{
		for (int i = 1; i <= n; ++i)
		{
			string code;
			int cur = i;
			int parent = _t[cur]->_parent;
			while (parent)
			{
				if (_t[parent]->_left == cur)
				{
					code += '0';
				}
				else
				{
					code += '1';
				}
				cur = parent;
				parent = _t[cur]->_parent;
			}
			reverse(code.begin(), code.end());
			_makeCodeList.insert(make_pair(_t[i]->_data, code));
			_translateCodeList.insert(make_pair(code, _t[i]->_data));
		}
	}

	int _num;// 记录有效节点个数
	vector<Node*> _t;// 顺序结果存储霍夫曼树节点
	unordered_map<char, string> _makeCodeList;// 编码列表
	unordered_map<string, char> _translateCodeList;// 译码列表
};

int main()
{
	int Q = 0;
	cin >> Q;
	HuffmanTree ht;
	while (Q--)
	{
		int T = 0;
		cin >> T;
		if (T == 0)
		{
			int n = 0;
			cin >> n;
			string s;
			for (int i = 0; i < n; ++i)
			{
				char ch = 0;
				cin >> ch;
				s += ch;
			}
			vector<int> v(n);
			for (auto& e : v)
			{
				cin >> e;
			}
			HuffmanTree tmp(n, s, v);
			tmp.swap(ht);
		}
		else if (T == 1)
		{
			string s;
			cin >> s;
			ht.MakeCode(s);
		}
		else if (T == 2)
		{
			string s;
			cin >> s;
			ht.TranslateCode(s);
		}
	}
	return 0;
}