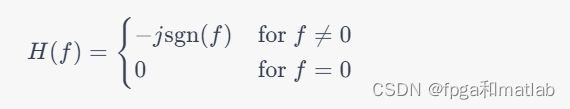信号的希尔伯特变换频谱分析matlab仿真
目录
一、理论基础
二、核心程序
三、仿真结论
一、理论基础
信号的希尔伯特变换频谱分析(Hilbert Transform Spectrum Analysis)是一种用于分析信号的时频特性的方法。它利用希尔伯特变换将信号转换为解析信号,然后通过对解析信号进行频谱分析来获得信号的时频分布。
步骤一:信号的希尔伯特变换 希尔伯特变换是一种线性变换,将一个实值信号转换为一个复值信号,该复值信号被称为解析信号。希尔伯特变换可以通过傅里叶变换的频域表达式来实现,数学公式如下:
其中,H(f)表示频域中的希尔伯特变换,j为虚数单位,text{sgn}(f)为符号函数,用于确定正负频率。
实现难点:
- 频域和时域的关系:希尔伯特变换是基于频域的操作,因此需要进行频域和时域之间的转换。这涉及到离散傅里叶变换(DFT)或快速傅里叶变换(FFT)等算法的使用。
- 零频率处理:希尔伯特变换中存在一个特殊情况,即当频率为零时,变换结果为零。在实际应用中,需要对这种情况进行特殊处理,以确保信号的完整性。
步骤二:解析信号的频谱分析 通过希尔伯特变换得到解析信号后,可以对其进行频谱分析,以获得信号的时频分布。常见的频谱分析方法包括短时傅里叶变换(STFT)和小波变换等。这些方法可以将信号分解为时域和频域的二维矩阵,表示信号在不同时间和频率上的能量分布。
实现难点:
- 分辨率和窗口选择:频谱分析涉及到选择合适的时间窗口大小和频率分辨率。较大的时间窗口可以提供更好的频率分辨率,但会导致时域分辨率下降;而较小的时间窗口则会提高时域分辨率,但频率分辨率下降。因此,选择合适的时间窗口大小和频率分辨率是一个需要平衡的问题。
- 信号边缘效应:频谱分析常常涉及到将信号分割为不同的时间段进行分析。在分割边缘处,由于信号的不连续性,可能会引入边缘效应,导致频谱分析结果不准确。因此,需要采取合适的边缘处理技术,如零填充或加窗等方法。
总结而言,希尔伯特变换频谱分析通过希尔伯特变换将信号转换为解析信号,并对解析信号进行频谱分析,实现对信号的时频特性分析。实现希尔伯特变换频谱分析的难点包括频域和时域的关系、零频率处理、分辨率和窗口选择以及信号边缘效应处理。克服这些难点可以实现准确且有效的时频特性分析。
步骤三:时频特性分析的可视化 在完成解析信号的频谱分析之后,需要将时频特性以可视化的方式呈现出来,以便进行分析和解释。常见的可视化方法包括时频图、频谱图和瀑布图等。
-
时频图:时频图将时间轴和频率轴结合起来,使用不同的颜色或亮度表示信号在不同时间和频率上的能量或振幅。时频图可以直观地显示信号的瞬时频率和能量分布,有助于观察信号的时频变化。
-
频谱图:频谱图将频率轴和能量或振幅轴结合起来,显示信号在不同频率上的能量或振幅分布。频谱图可以清晰地展示信号的频率成分和强度,有助于分析信号的频域特性。
-
瀑布图:瀑布图结合了时频图和频谱图的特点,以三维形式呈现信号的时频特性。瀑布图在时间、频率和能量或振幅三个维度上进行可视化,可以更全面地展示信号的时频变化和频域分布。
实现难点:
-
可视化参数的选择:时频特性的可视化需要选择合适的参数,如颜色映射、坐标轴刻度和标签等。合理选择这些参数可以更好地展示时频特性,但需要综合考虑视觉效果和数据解读的需求。
-
大数据量的处理:当信号的采样率较高或者时间序列较长时,可能会产生大量的数据,对于这些大数据量的处理和可视化需要高效的算法和工具支持。
-
可视化结果的解释:时频特性的可视化结果需要进行解释和分析,以揭示信号的特点和含义。对于复杂的时频特性,如瞬时频率的变化、频率的跟踪等,需要进行专业的分析和解释。
总结而言,希尔伯特变换频谱分析的最后一步是将时频特性可视化呈现。常见的可视化方法包括时频图、频谱图和瀑布图等,用于展示信号的时频特性。实现时频特性的可视化的难点包括可视化参数的选择、大数据量的处理以及可视化结果的解释。通过克服这些难点,可以更好地理解和分析信号的时频特性。
二、核心程序
..................................................................................
close all;clear all;clc;
fs=60;
%--------------------------------------------------
dt=1/fs;
t=0:dt:1-dt;
sigt=cos(2*pi*10*t);
[f,sigf]=Time2FrequencyDomain(t,sigt);
[tb,sigtb]=Frequency2TimeDomain(f,sigf);
figure;
subplot(211)
plot(t,sigtb);hold on;
plot(t,sigt,'r--')
legend('time2frequence','frequence2time')
subplot(212)
plot(f(length(f)/2+1:length(f)),sigf(length(f)/2+1:length(f)));%(length(f)/2+1:length(f))
legend('信号频谱')
disp('时域角度计算的能量及功率:')
[Et,Pt]=SignalEnergeAndPowerInTime(sigt,dt);
Et ,Pt
disp('频域角度计算的能量及功率:')
[Ef,Pf]=SignalEnergeAndPowerInFrequence(sigt,t);
Et ,Pt
%-----------------------------------------------------
% am信号调制解调0
T=3;fm=1;A=2;a=1.5;fc=10;
[am,tam,mt]=CreateAm(fs,T,fm,A,fc,a);
[amf,amfs]=Time2FrequencyDomain(tam,am);%am调制信号的频谱
ampfs=abs(amfs).^2/T;
[tdam,dam]=CoherenceDemodulateAm(am,fm,fc,tam);%am相干解调
PlotAmandDemodulated(mt,dam,tdam,amf,ampfs);
up2165三、仿真结论