力扣刷题——二叉树
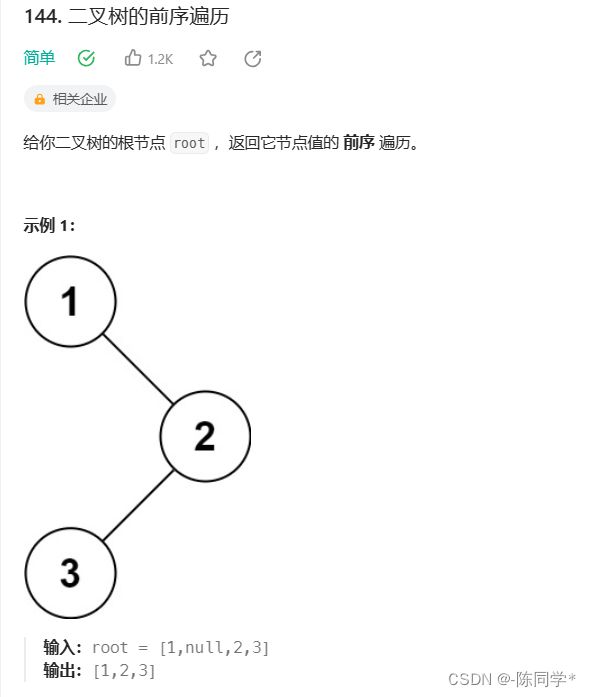
力扣刷题144 二叉树的前序遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector preorderTraversal(TreeNode* root) {
vector v;
stack s;
TreeNode* p=root;
while(!s.empty()||p){
if(p){
s.push(p);
v.push_back(p->val);
p=p->left;
}
else{
p=s.top();
s.pop();
p=p->right;
}
}
return v;
}
}; 力扣刷题94 二叉树得中序遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector inorderTraversal(TreeNode* root) {
stack s;
TreeNode* p= root;
vector v;
while(p||!s.empty()){
if(p){
s.push(p);
p=p->left;
}
else{
p=s.top();
s.pop();
v.push_back(p->val);
p=p->right;
}
}
return v;
}
}; 力扣刷题145二叉树的后序遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector postorderTraversal(TreeNode* root) {
vectorv;
stacks;
TreeNode* p=root;
TreeNode* r= NULL;
while(p||!s.empty()){
if(p){
s.push(p);
p=p->left;
}
else{
p=s.top();
if(p->right&&p->right!=r){
p=p->right;
}
else{
s.pop();
v.push_back(p->val);
r=p;
p=NULL;
}
}
}
return v;
}
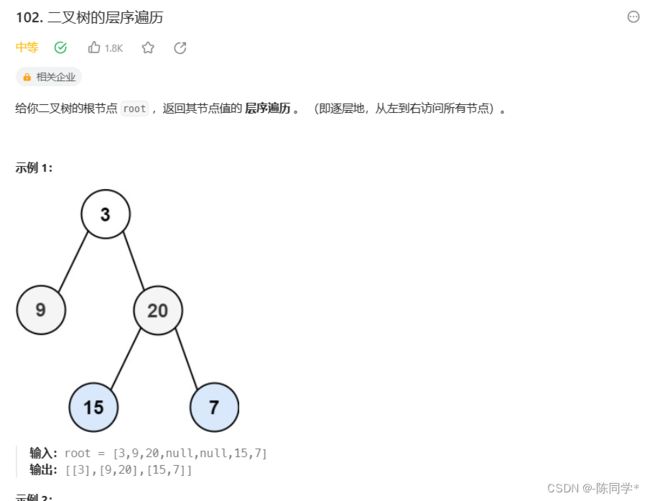
}; 力扣刷题102二叉树的层次遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector> levelOrder(TreeNode* root) {
vector> res;
vector t;
queue Q;
int size=0;
if(root==NULL) return res;
Q.push(root);
while(!Q.empty()){
size = Q.size();
t.clear();
for(int i=0;ival);
if(Q.front()->left) Q.push(Q.front()->left);
if(Q.front()->right) Q.push(Q.front()->right);
Q.pop();
}
res.push_back(t);
}
return res;
}
}; 力扣刷题107自底向上的层次遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector> levelOrderBottom(TreeNode* root) {
vector> res;
vector t;
queue Q;
int size=0;
if(root==NULL) return res;
Q.push(root);
while(!Q.empty()){
size = Q.size();
t.clear();
for(int i=0;ival);
if(Q.front()->left) Q.push(Q.front()->left);
if(Q.front()->right) Q.push(Q.front()->right);
Q.pop();
}
res.push_back(t);
}
reverse(res.begin(),res.end());
return res;
}
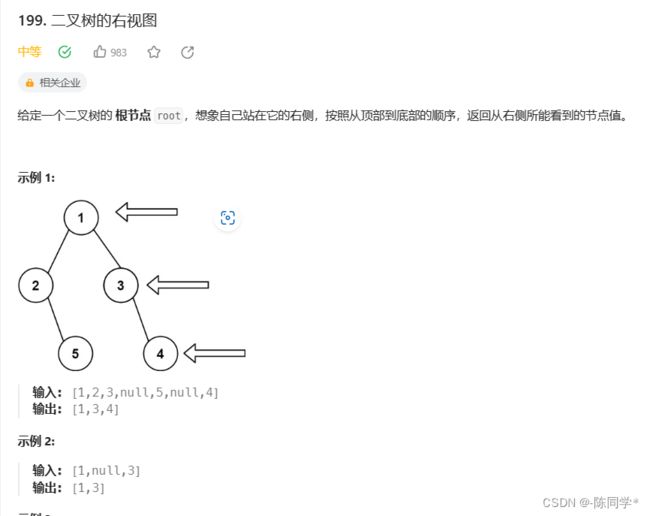
}; 力扣刷题199二叉树的右视图
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector rightSideView(TreeNode* root) {
vector t;
queue Q;
int size=0;
if(root==NULL) return t;
Q.push(root);
while(!Q.empty()){
size = Q.size();
for(int i=0;ival);
if(Q.front()->left) Q.push(Q.front()->left);
if(Q.front()->right) Q.push(Q.front()->right);
Q.pop();
}
}
return t;
}
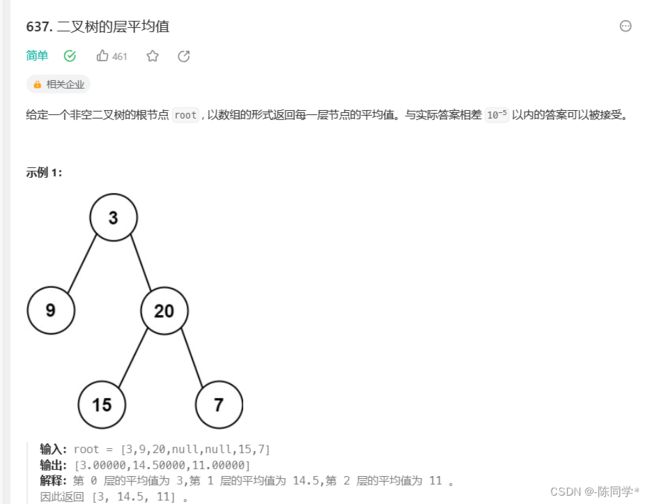
}; 力扣刷题637二叉树的层平均值
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector averageOfLevels(TreeNode* root) {
vector t;
queue Q;
int size=0;
long long sum=0;//可能会超过int
if(root==NULL) return t;
Q.push(root);
while(!Q.empty()){
size = Q.size();
sum=0;
for(int i=0;ival;
if(Q.front()->left) Q.push(Q.front()->left);
if(Q.front()->right) Q.push(Q.front()->right);
Q.pop();
}
double av=(double)sum/size;
t.push_back(av);
}
return t;
}
}; 力扣刷题429 N叉树的层次遍历
/*
// Definition for a Node.
class Node {
public:
int val;
vector children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
vector> levelOrder(Node* root) {
vector t;
vector> res;
queue Q;
int size=0;
if(root==NULL) return res;
Q.push(root);
while(!Q.empty()){
size = Q.size();
t.clear();
for(int i=0;ival);
for(int j=0;jchildren.size();j++){
if(node->children[j]!=NULL) Q.push(node->children[j]);
}
}
res.push_back(t);
}
return res;
}
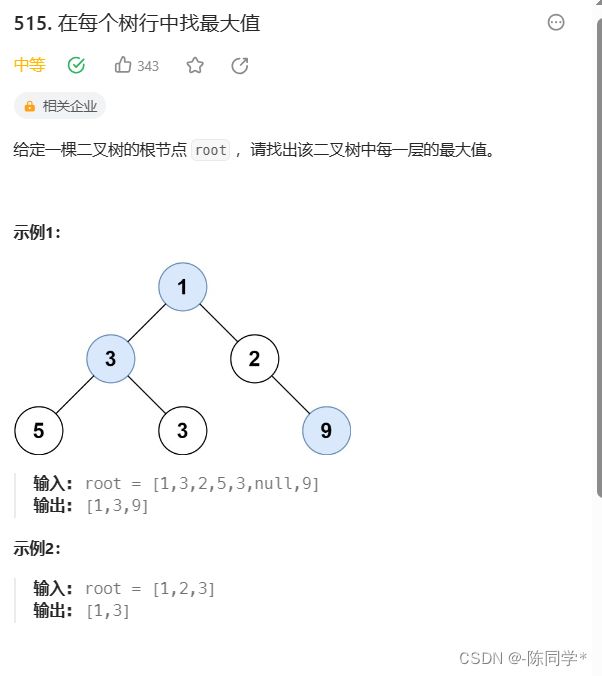
}; 力扣刷题515在每个树行中找最大值
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector largestValues(TreeNode* root) {
vector t;
queue Q;
TreeNode* p=root;
if(p) Q.push(root);
while(!Q.empty()){
int size=Q.size();
int max_val=INT_MIN;
for(int i=0;ival);
if(p->left) Q.push(p->left);
if(p->right) Q.push(p->right);
Q.pop();
}
t.push_back(max_val);
}
return t;
}
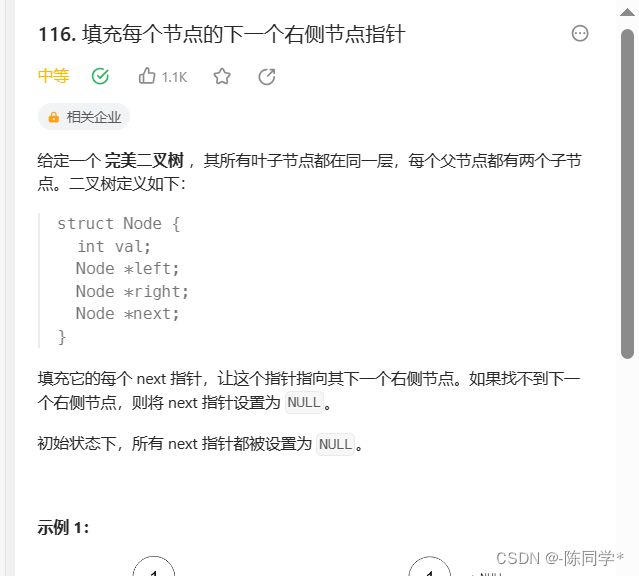
}; 力扣刷题116
/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node* next;
Node() : val(0), left(NULL), right(NULL), next(NULL) {}
Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}
Node(int _val, Node* _left, Node* _right, Node* _next)
: val(_val), left(_left), right(_right), next(_next) {}
};
*/
class Solution {
public:
Node* connect(Node* root) {
queueQ;//定义一个队列
Node* pre,*p;
int size;
if(root) Q.push(root);
while(!Q.empty()){
size=Q.size();
for(int i=0;inext=p;
pre=pre->next;
}
if(p->left) Q.push(p->left);
if(p->right) Q.push(p->right);
}
pre->next = NULL;
}
return root;
}
}; 力扣刷题104最大深度
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void maxdpt(TreeNode* root,int &maxdepth,int d){
if(root){
maxdpt(root->left,maxdepth,d+1);
maxdpt(root->right,maxdepth,d+1);
maxdepth=max(maxdepth,d);
}
}
int maxDepth(TreeNode* root) {
int maxdepth=0,d=1;
maxdpt(root,maxdepth,d);
return maxdepth;
}
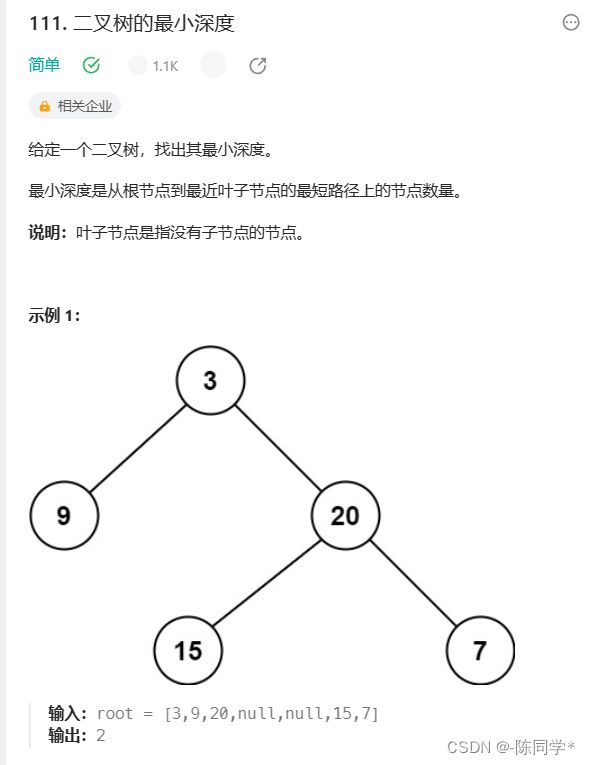
};力扣刷题111二叉树最小深度
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void mindpt(TreeNode* root,int &mindepth,int d){
if(root){
mindpt(root->left,mindepth,d+1);
mindpt(root->right,mindepth,d+1);
//需要注意的是,只有当左右孩子都为空的时候,才说明遍历的最低点了。如果其中一个孩子为空则不是最低点
if(root->left==NULL&&root->right==NULL) mindepth=min(mindepth,d);
}
}
int minDepth(TreeNode* root) {
if(root==NULL) return 0;
int mindepth=INT_MAX;
int d=1;
mindpt(root,mindepth,d);
return mindepth;
}
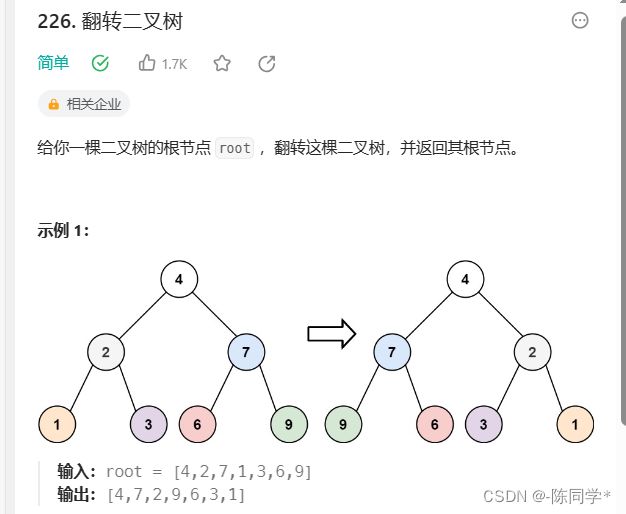
};力扣刷题226翻转二叉树
这道题目使用前序遍历和后序遍历都可以,唯独中序遍历不方便,因为中序遍历会把某些节点的左右孩子翻转了两次!建议拿纸画一画,就理解了
那么层序遍历可以不可以呢?依然可以的!只要把每一个节点的左右孩子翻转一下的遍历方式都是可
以的!
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if (root == NULL) return root;
invertTree(root->left); // 左
swap(root->left, root->right); // 中
invertTree(root->left); // 右
return root;
}
};class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
queue que;
if (root != NULL) que.push(root);
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
swap(node->left, node->right); // 节点处理
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return root;
}
}; 力扣刷题101对称二叉树
class Solution {
public:
bool compare(TreeNode* left, TreeNode* right) {
// 首先排除空节点的情况
if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
// 排除了空节点,再排除数值不相同的情况
else if (left->val != right->val) return false;
// 此时就是:左右节点都不为空,且数值相同的情况
// 此时才做递归,做下一层的判断
bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右
bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左
bool isSame = outside && inside; // 左子树:中、 右子树:中 (逻辑处理)
return isSame;
}
bool isSymmetric(TreeNode* root) {
if (root == NULL) return true;
return compare(root->left, root->right);
}
};力扣刷题110平衡二叉树
分别求出其左右子树的高度,然后如果差值小于等于1,则返回当前二叉树的高度,否则返回-1,表示已经不是二叉平衡树了。
class Solution {
public:
int getHeight(TreeNode* node) {
//空节点
if(!node) return 0;
int left = getHeight(node->left);
if(left==-1) return -1;//往上返回
int right= getHeight(node->right);
if(right==-1) return -1;
return abs(left-right)>1?-1:max(left,right)+1;
}
bool isBalanced(TreeNode* root) {
return getHeight(root)==-1? false:true;
}
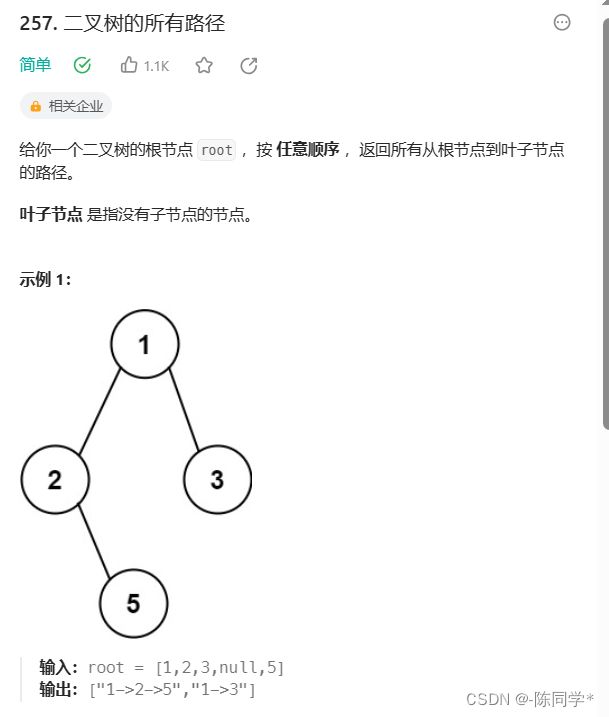
};力扣刷题257二叉树的所有路径
class Solution {
public:
void allPath(TreeNode* root,vector& t,vector&path){
if(!root) return;
t.push_back(root->val);
if(!root->left&&!root->right){
string ss="";
for(int i=0;ileft,t,path);
allPath(root->right,t,path);
t.pop_back();
}
vector binaryTreePaths(TreeNode* root) {
vector t;
vector path;
allPath(root,t,path);
return path;
}
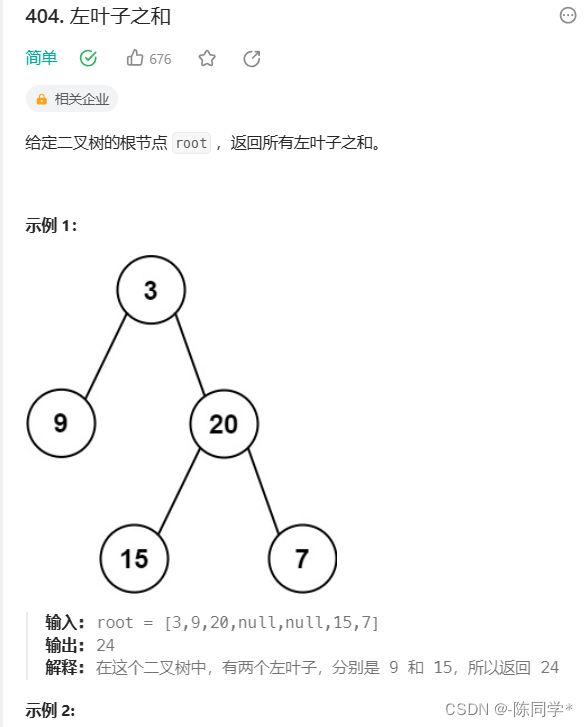
}; 力扣刷题404左叶子之和
class Solution {
public:
void add (TreeNode* root,int &sum){
if(!root) return;
if(root->left&&!root->left->left&&!root->left->right){
sum+=root->left->val;
}
add(root->left,sum);
add(root->right,sum);
}
int sumOfLeftLeaves(TreeNode* root) {
int sum=0;
if(root==nullptr) return 0;
add(root,sum);
return sum;
}
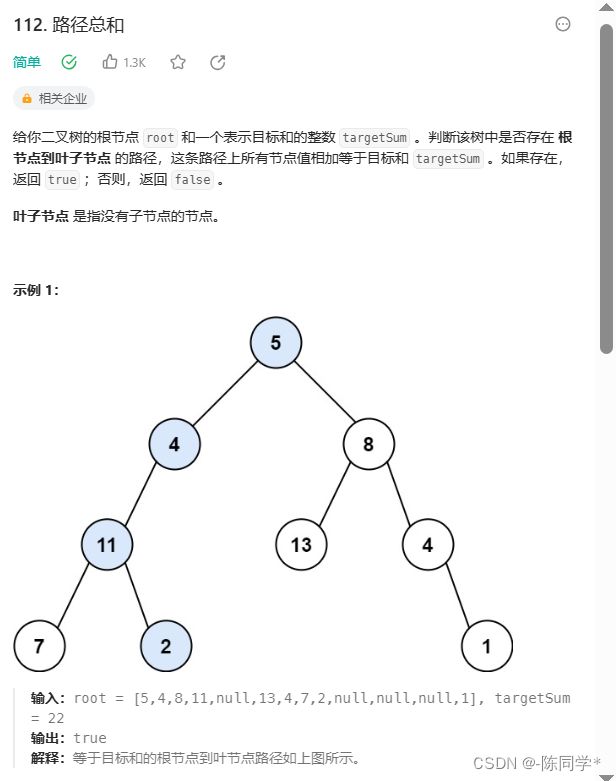
};力扣刷题112路经总和
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if(!root) return false;
if(!root->left&&!root->right&&targetSum==root->val) return true;
return hasPathSum(root->left,targetSum-root->val)||hasPathSum(root->right,targetSum-root->val);
}
};力扣106中序和后序构造二叉树
力扣刷题654最大二叉树
class Solution {
public:
TreeNode* create(vectornums,int left,int right){
if(left>right) return nullptr;
int maxindex=left;
for(int i=left;i<=right;i++) {
if(nums[i]>nums[maxindex]) maxindex=i;
}
TreeNode* node= new TreeNode(nums[maxindex]);
node->left=create(nums,left,maxindex-1);
node->right=create(nums,maxindex+1,right);
return node;
}
TreeNode* constructMaximumBinaryTree(vector& nums) {
return create(nums,0,nums.size()-1);
}
}; 力扣刷题617合并二叉树
class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if(!root1) return root2;
if(!root2) return root1;
root1->val+=root2->val;
root1->left=mergeTrees(root1->left,root2->left);
root1->right=mergeTrees(root1->right,root2->right);
return root1;
}
};力扣刷题700二叉搜索树中的搜索
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if (root == NULL) return root;
invertTree(root->left); // 左
swap(root->left, root->right); // 中
invertTree(root->right); // 右
return root;
}
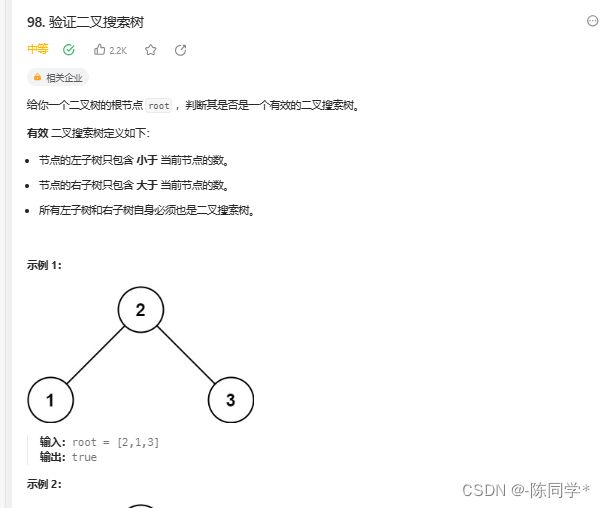
};力扣刷题98判断是否是二叉排序树
力扣刷题530二叉搜索树的最小绝对差
class Solution {
public:
TreeNode* pre;
void Getmin(TreeNode* p,int &mind){
if(!p) return ;
Getmin(p->left,mind);
if(pre&&mind>abs(p->val-pre->val)) mind=abs(p->val-pre->val);
pre=p;
Getmin(p->right,mind);
}
int getMinimumDifference(TreeNode* root) {
int mind=INT_MAX;
pre=nullptr;
Getmin(root,mind);
return mind;
}
};力扣刷题501二叉搜索树的众数
class Solution {
public:
vector res;
TreeNode* pre;
int count;
int maxcount;
void MyfindMode(TreeNode* root) {
if(!root) return ;
MyfindMode(root->left);
if (pre&&pre->val==root->val) count++;
else count=1;
if(count==maxcount){
res.push_back(root->val);
}
else if(count>maxcount){
maxcount=count;
res.clear();
res.push_back(root->val);
}
pre=root;
MyfindMode(root->right);
}
vector findMode(TreeNode* root){
count=0;
maxcount=0;
MyfindMode(root);
return res;
}
}; 力扣刷题236二叉树的最近公共祖先
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root==NULL||root==p||root==q) return root;
TreeNode* l=lowestCommonAncestor(root->left,p,q);
TreeNode* r=lowestCommonAncestor(root->right,p,q);
if(!l) return r;
if(!r) return l;
return root;
}
};力扣701二叉搜索树中的插入操作
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if(!root) {
TreeNode* node=new TreeNode(val);
return node;
}
if(root->val>val) root->left = insertIntoBST(root->left,val);
if(root->valright = insertIntoBST(root->right,val);
return root;
}
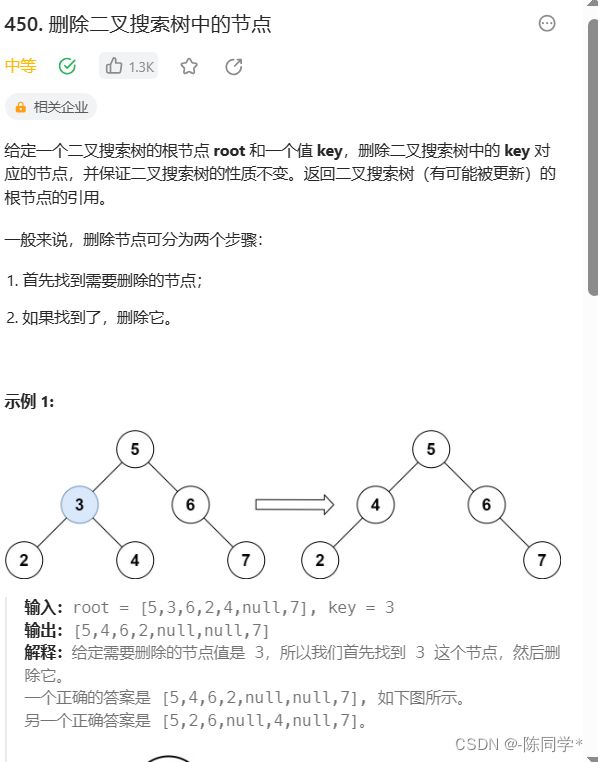
}; 力扣刷题450删除搜索二叉树的节点
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
//递归出口1:没找到
if(!root) return nullptr;
//递归出口2:找到
if(root->val==key) {
//删除的是叶子
if(root->left==nullptr&&root->right==nullptr){
return nullptr;//其实达到了让叶子的父亲的指针指向NULL的效果
}
//删除节点左空右不空
else if(root->left==nullptr&&root->right){
return root->right;//其实达到了让root的父亲的指针指向root->right的效果
}
//删除的节点左不空右空
else if(root->left&&root->right==nullptr){
return root->left;//其实达到了让root的父亲的指针指向root->left的效果
}
//删除的节点的孩子均不空
else{
//首先找到后继
TreeNode* cur=root->right;
while(cur->left){
cur=cur->left;
}
cur->left=root->left;
//此时的情况属于左为空右不为空
return root->right;
}
}
//递归逻辑
//单层递归中传入的是root的左(右)子树,返回的是删除val以后的左(右)子树
if(keyval) root->left =deleteNode(root->left,key);
if(key>root->val) root->right = deleteNode(root->right,key);
return root;
}
}; 力扣刷题669修建二叉搜索树
lass Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if(!root) return nullptr;
if(root->valright,low,high);
else if(root->val>high) return trimBST(root->left,low,high);
root->left=trimBST(root->left,low,high);
root->right=trimBST(root->right,low,high);
return root;
}
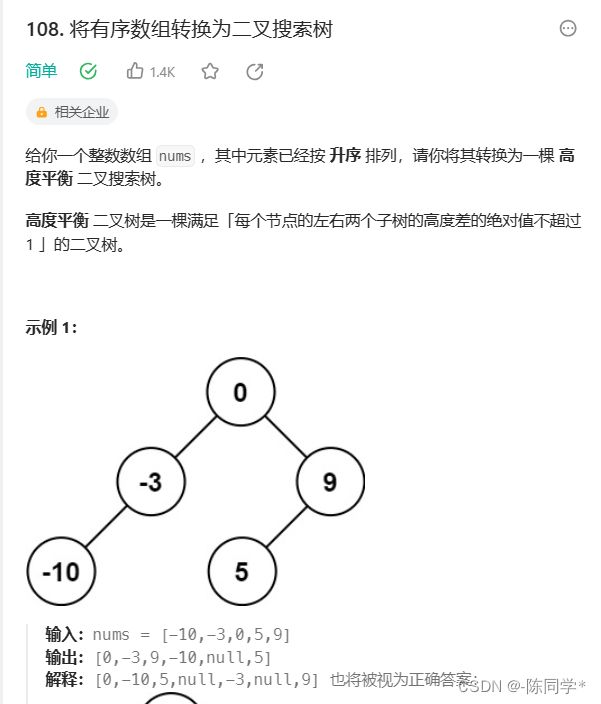
}; 力扣刷题108将有序数组转换为二叉搜索树
lass Solution {
public:
//左闭右闭
TreeNode* func(vectornums,int left,int right){
//非法区间
if(left>right) return nullptr;
//取中间值
int mid = (left+right)/2;
TreeNode* root= new TreeNode(nums[mid]);
root->left=func(nums,left,mid-1);
root->right=func(nums,mid+1,right);
return root;
}
TreeNode* sortedArrayToBST(vector& nums) {
return func(nums,0,nums.size()-1);
}
}; 力扣刷题538将二叉搜索树转为累加树
lass Solution {
public:
TreeNode* pre;
TreeNode* convertBST(TreeNode* &root) {
if(!root) return nullptr;
convertBST(root->right);
if(pre)
root->val+=pre->val;
pre=root;
convertBST(root->left);
return root;
}
};