数据结构——堆

1.堆的定义 

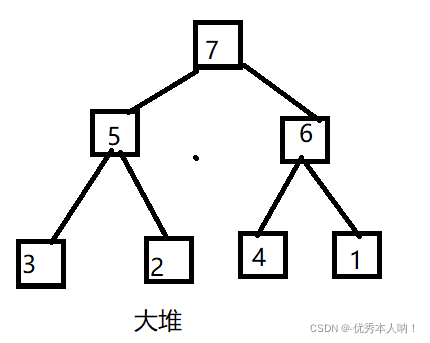
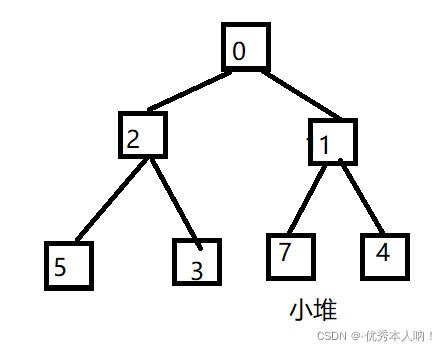
          堆（heap）是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树(逻辑层面上)的数组对象(物理层面上),常用来在一组变化频繁(发生增删查改的频率较高)的数据中寻找最值.将根结点最大的堆叫做最大堆或大根堆，这样可以找到堆中的最大值(根节点的值);根结点最小的堆叫做最小堆或小根堆,这样可以找到堆中的最小值。

2.堆在物理上和逻辑上的相互转换

3.堆的核心操作——向下调整

        要实现向下调整,需要满足的前提是:针对某个结点(某个下标)进行向下调整时,除了该结点和其左右孩子之外,该完全二叉树的其余部分应该确保已经满足堆的性质.

堆的性质:

(1) 堆中某个结点的值总是不大于或不小于其父结点的值；

(2) 堆总是一棵完全二叉树。

❤向下调整的具体操作步骤(假设构建的堆是小堆):

(1)明确要调整结点的下标位置是不是叶子结点的下标,如果是叶子结点,操作结束;反之,继续下一步操作;

(2)标记要调整结点的左右两个孩子的值,找到其中的最小值(因为这棵树是一棵完全二叉树,所以不可能出现有左孩子没有右孩子的情况).该结点只有左孩子,没有右孩子,所以最小值的下标可以直接设置为左孩子的下标.

(注:左右孩子的下标都需要小于size,否则会越界.如果结点的左孩子的下标>=size,说明该结点是叶子结点,反之该结点有孩子,不是叶子结点)

(3)将左右孩子的最小值与要调整结点的下标进行比较

结点的值 < = 孩子的最小值 ->在满足前提下,需要调整的位置也满足堆的性质,操作结束

结点的值 > 孩子的最小值 -> 进行下一步操作

(4)将结点和孩子的最小值进行交换

(5)判断交换之后,结点是否还满足堆的性质,如果不满足,继续执行第一步(1).(可以用循环来实现)

循环的两个出口:

(1) 要调整的结点是叶子结点;

(2) 要调整的位置已经满足堆的性质.

❤代码实现:

    public static void shiftDown(long[] array,int size,int index){
        while(true){
            //设置左孩子的下标
            int left = 2 * index + 1;
            //左孩子符合范围，该结点不是叶子，否则是叶子
            if(left >= size){
                //是叶子，直接结束操作，return返回
                return;
            }
            //不是叶子，判断该结点是否有右孩子
            int right = left + 1;
            //假设左右孩子中的最小值的下标为min，将其置为左孩子的下标
            int min = left;
            if(right < size && array[right] < array[left]){
                //有右孩子的前提下,右孩子的值小于左孩子,说明最小值为右孩子的值,
                // 那么将最小值的下标置为右孩子的下标
                min = right;
            }
            //将最值和要调整位置的值进行比较,满足堆的性质,调整结束
            if(array[index] <= array[min]){
                return;
            }
            //不满足堆的性质,交换两个位置的值
            long t = array[index];
            array[index] = array[min];
            array[min] = t;
            //更新最小值的下标
            index = min;
        }
    }

4.实现任意一个完全二叉树的建堆操作

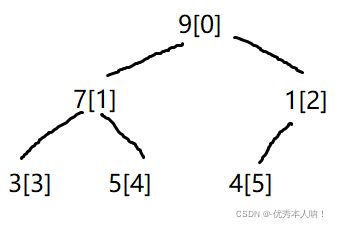
对于任意一棵二叉树要实现建堆操作,简单来说就是从叶子节点从后到前实现向下调整即可.叶子结点向下调整还是该位置,因此可以从第一个非叶子节点实现向下调整操作.

在上图中,叶子结点的下标分别为[5],[4],[3],从后到前第一次遇到非叶子结点的下标为[2],该树中最后一个元素结点的下标为[5](也就是[size - 1]),如果要通过计算来确定非叶子结点的下标,即算式是     (5 - 1)  / 2 = 2,带入size - 1,可以得到非叶子结点的下标 = ((size - 1) - 1 ) / 2 = (size - 2) / 2.

❤代码实现:

    public static void BuildHeap(long[] array,int size){
        //最后一个结点下标为size - 1
        //双亲的下标一定是(size - 2) / 2
        for(int i = (size - 2) / 2;i >= 0;i--){
            shiftDown(array,size,i);
        }
    }

 5.以小堆实现优先级队列

(1)优先级队列的定义

优先级队列（priority queue） 是0个或多个元素的集合，每个元素都有一个优先权，对优先级队列执行的操作有查找(peek())，插入(offer(e))和删除(poll())。一般情况下，查找操作用来搜索优先权最大的元素，删除操作用来删除该元素 。对于优先权相同的元素，可按先进先出次序处理或按任意优先权进行。

(2)实现前提:优先级队列中的元素要求具备比较能力。

(3)典型使用场景：OS调度进程时，进程进程选择

❤代码实现：

    private long[] array;
    private int size;
    public int size(){
        return size;
    }
    public boolean isEmpty(){
        return size == 0;
    }
    public MyPriorityQueue(){
        //构造方法
        array = new long[2];
        size = 0;
    }
    public void offer(long e){
        ensureCapacity();
        array[size] = e;
        size++;
        shiftUp(array,size - 1);
    }
    public long peek(){
        if(size < 0){
            throw new RuntimeException("队列是空的");
        }
        return array[0];
    }
    public long poll(){
        if(size < 0){
            throw new RuntimeException("队列是空的");
        }
        long e = array[0];
        array[0] = array[size - 1];
        array[size - 1] = 0;
        size--;
        shiftDown(array,size,0);
        return e;
    }

    private void shiftDown(long[] array, int size, int index) {
        while(2 * index + 1 < size){
            int min = 2 * index + 1;
            int right = min + 1;
            if(right < size && array[right] < array[min]){
                min = right;
            }
            if(array[index] <= array[min]){
                return;
            }
            swap(array,index,min);
            index = min;
        }
    }

    private void swap(long[] array, int i, int j) {
        long t = array[i];
        array[i] = array[j];
        array[j] = t;
    }

    private void shiftUp(long[] array, int index) {
        while(index != 0){
            int parent = (index - 1) / 2;
            if(array[parent] <= array[index]){
                return;
            }
            swap(array,index,parent);
            index = parent;
        }
    }

    private void ensureCapacity() {
        if(size < array.length){
            return;
        }
        array = Arrays.copyOf(array,array.length * 2);
    }
    public void check(){
        if(size < 0 || size > array.length){
            throw new RuntimeException("size约束出错");
        }
        //满足小堆的特点
        for (int i = 0; i < size; i++) {
            int left = 2 *i + 1;
            int right = 2 * i + 2;
            if(left >= size){
                continue;
            }
            if(array[i] > array[left]){
                throw new RuntimeException(String.format("[%d]位置的值大于其左孩子的值了",i));
            }
            if(right < size && array[i] > array[right]){
                throw new RuntimeException(String.format("[%d]位置的值大于其右孩子的值了",i));
            }
        }
    }

6.比较数组实现和堆实现优先级队列的性能

❤数组实现代码：

    private long[] array;
    private int size;
    public MyPriorityQueue2(){
        array = new long[10];
        size = 0;
    }
    public void offer(long e){
        ensureCapacity();
        array[size++] = e;
    }
    public long peek(){
        int minIndex = 0;
        for (int i = 1; i < size; i++) {
            if(array[i] < array[minIndex]){
                minIndex = i;
            }
        }
        return array[minIndex];
    }
    public long poll(){
        int minIndex = 0;
        for (int i = 1; i < size; i++) {
            if(array[i] < array[minIndex]){
                minIndex = i;
            }
        }
        long e = array[minIndex];
        array[minIndex] = array[size - 1];
        array[size - 1] = 0;
        size--;
        return e;

    }

    private void ensureCapacity() {
        if(size < array.length){
            return;
        }
        array = Arrays.copyOf(array,array.length * 2);
    }

时间复杂度	offer（e）	peek（）	poll（）
数组实现	O（1）	O（n）	O（n）
堆实现	O（logn）	O（1）	O（logn）

按照上述分析，我们可以得知在实现优先级队列中，堆实现比数组实现效率更高（在数据集很大的情况下）。

7.Top-K问题

（1）该问题实现的目的：在一组数据集中找到最大（或最小）的前K个数据（k远远小于数据集的个数n）。

（2）问题分析：

思路一：先定义一个k大小的容器，遍历数据集，通过循环比较，找出数据集中最大（或最小）的前k个元素放入k大小的容器中，放入的数据不用考虑顺序问题。

思路二：先对数据集进行排序，取出前k个元素。

注：思路一和思路二的时间复杂度较大，在数量较大的数据集中查找的速度较慢，不考虑采用。

思路三：使用堆解决该问题。如果要找出最大值，那么需要我们建一个小堆（原因：首先需要取出前k个元素，找出这k个元素中的最小值，与剩余的元素进行比较，如果比剩余的元素小，将其替换，继续找出这k个元素中的最小值，因此需要建立一个小堆来寻找数据集中的最大的前k个元素）；反之建一个大堆。

❤代码实现：

    public int[] smallestK(int[] arr, int k) {
        if(k == 0){
            return new int[0];
        }
        PriorityQueue pq = new PriorityQueue<>((o1, o2) -> o2 - o1);
        for(int i = 0;i < arr.length;i++){
            //当pq的个数小于k时，说明k容器中还没有放满
            if(pq.size() < k){
                pq.offer(arr[i]);
            }else if(arr[i] < pq.peek()){
                //说明放满了，并且现在pq里的最大值大于数组中剩余元素的值
                //需要将其取出，放入更小的值
                pq.poll();
                pq.offer(arr[i]);
            }
        }
        //定义一个有k容量的容器
        int[] ans = new int[k];
        //遍历该容器，将里面的元素取出
        for(int i = 0;i < k;i++){
            ans[i] = pq.poll();
        }
        return ans;
    }