算法:二叉平衡树(AVL树)
平衡二叉树定义
平衡二叉树 全称叫做 平衡二叉搜索(排序)树,简称 AVL树。英文:Balanced Binary Tree (BBT),注:二叉查找树(BST)
AVL 什么意思?AVL 是大学教授 G.M. Adelson-Velsky 和 E.M. Landis 名称的缩写,他们提出的平衡二叉树的概念,为了纪念他们,将 平衡二叉树 称为 AVL树。
AVL树本质上是一颗二叉查找树,但是它又具有以下特点:
- 可以是空树。 假如不是空树,任何一个结点的左子树与右子树都是平衡二叉树,并且高度之差的绝对值不超过 1
- 左右两个子树 也都是一棵平衡二叉树。
- 在AVL树中,任何节点的两个子树的高度最大差别为 1 ,所以它也被称为平衡二叉树 。
为什么要有平衡二叉树
二叉查找树是最常用的一种二叉树,它支持快速插入、删除、查找操作,各个操作的时间复杂度跟树的高度成正比,理想情况下,时间复杂度是 O(logn)。
不过,二叉查找树在频繁的动态更新过程中,可能会出现树的高度远大于 log n 的情况,从而导致各个操作的效率下降。极端情况下,二叉树会退化为链表,时间复杂度会退化到O(n)。
举一个例子,以这样一个数组为例 [42,37,18,12,11,6,5] 构建一棵二叉搜索树,由于数组中任意一点都可以作为二叉搜索树的根节点,因此这棵二叉搜索树并不唯一
我们来看一个极端的例子(以42作为根节点,顺序插入元素)

在这个例子中,二叉搜索树退化成了链表,搜索的时间复杂度为 O(n),失去了作为一棵二叉搜索树的意义。
为了让二叉搜索树不至于太“倾斜”,我们需要构建一棵平衡二叉搜索树

可以看出,平衡二叉搜索树的搜索时间复杂度为O(logn),避免了因为随机选取根节点构建二叉搜索树而可能造成的退化成链表的情况。
总结:
- 平衡二叉树的严格定义是这样的:二叉树中任意一个节点的左右子树的高度相差不能大于1。
- 发明平衡二叉树的这类数据结构的初衷是,解决普通二叉树在频繁的插入、删除等动态更新的情况下,出现时间复杂度退化的问题。
- 平衡二叉查找树中“平衡”的意思,其实就是让整棵树左右看起来比较“对称”、比较“平衡”,不要出现左子树很高、右子树很矮的情况。这样就能让整棵树的高度相对来说低一点,响应的插入、删除、查找等操作的效率高一点
ps:最先被发明的平衡二叉查找树是AVL树,它是一种高度平衡的二叉查找树。但是很多平衡二叉查找树其实并没有严格符合上面的定义(树中任意一个节点的左右子树的高度相差不能大于 1),只要树的高度不比log n 大很多而且满足二叉查找树的定义,我们就可以说它是一种平衡二叉查找树,比如红黑树
这货还是不是平衡二叉树?
判断一棵平衡二叉查找树(AVL树)有如下必要条件:
- 条件一:必须是二叉搜索树。
- 条件二:每个节点的左子树和右子树的高度差至多为1。
平衡因子
平衡因子(bf):结点的左子树的深度减去右子树的深度。
即: 结点的平衡因子 = 左子树的高度 - 右子树的高度。
在 AVL树中,所有节点的平衡因子都必须满足: -1<=bf<=1;
- 红黑树中,通过红色节点和黑色节点作为辅助,来判断一颗二叉树是否相对平衡

- AVL树当中,我们通过“平衡因子”来判断一颗二叉树是否符合高度平衡。只有当二叉树所有结点的平衡因子都是-1, 0, 1这三个值的时候,这颗二叉树才是一颗合格的AVL树。

当插入或者删除节点时,会改变父节点的平衡因子

上图原本是一个平衡的AVL树,当插入了新结点1时,父结点2的平衡因子变成了1,祖父结点4的平衡因子变成了2。
最小不平衡子树:距离插入节点最近的,且平衡因子的绝对值大于1的节点为根的子树。
如何保持平衡二叉树平衡?
当插入或者删除节点的时候,可能打破avl树的平衡。
我们 可以通过旋转使之变平衡。有两种基本的旋转:
两种基本操作
左旋
右旋
那avl树什么时候进行左旋,什么时候进行右旋呢?
四种情况
有四种插入情况可能导致二叉查找树不平衡,分别为:
- LL:插入一个新节点到根节点的左子树(Left)的左子树(Left),导致根节点的平衡因子由1变为2
- RR:插入一个新节点到根节点的右子树(Right)的右子树(Right),导致根节点的平衡因子由-1变为-2
- LR:插入一个新节点到根节点的左子树(Left)的右子树(Right),导致根节点的平衡因子由1变为2
- RL:插入一个新节点到根节点的右子树(Right)的左子树(Left),导致根节点的平衡因子由-1变为-2
LL
示例1
示例2
示例3
/**
* 进行一次单右旋转
*
* @param node 最小失衡树根节点
*/
private AVLTreeNode<T> rightRotation(AVLTreeNode<T> node) {
AVLTreeNode<T> left = node.left;
node.left = left.right;
left.right = node;
// 更新高度
node.height = Math.max(height(node.left), height(node.right)) + 1;
left.height = Math.max(height(left.left), height(left.right)) + 1;
return left;
}
RR
/**
* 进行一次单左旋转
*
* @param node 最小失衡树根节点
*/
private AVLTreeNode<T> leftRotation(AVLTreeNode<T> node) {
AVLTreeNode<T> right = node.right;
node.right = right.left;
right.left = node;
// 更新高度
node.height = Math.max(height(node.left), height(node.right)) + 1;
right.height = Math.max(height(right.left), height(right.right)) + 1;
return right;
}
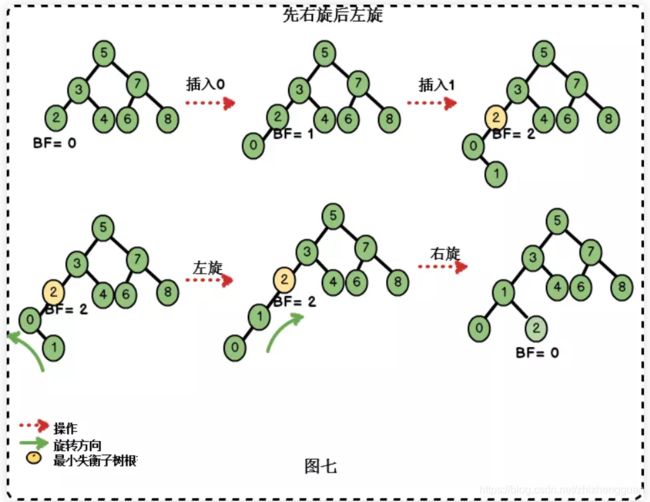
RL
/**
* 先右旋后左旋
*
* @param node 失衡树根节点
* @return 旋转后的根节点
*/
private AVLTreeNode<T> rightLeftRotation(AVLTreeNode<T> node) {
node.right = rightRoation(node.right);
return leftRoation(node);
}
LR
/**
* 先左旋后右旋
*
* @param node 失衡树根节点
* @return 旋转后的根节点
*/
private AVLTreeNode<T> leftRightRotation(AVLTreeNode<T> node) {
node.left = leftRoation(node.left);
return rightLeftRoation(node);
}
树的高度和深度本质区别:深度是从根节点数到它的叶节点,高度是从叶节点数到它的根节点。
代码实现
实现一[待续]
package main
import (
"fmt"
)
func abs(i int) int {
if i < 0 {
return -i
}
return i
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
type AvlNode struct {
key Hashable
value interface{}
height int
left *AvlNode
right *AvlNode
}
func (self *AvlNode) Key() Hashable{
return self.key
}
func (self *AvlNode) Value() interface{} {
return self.value
}
func (self *AvlNode) Height() int {
if self == nil {
return 0
}
return self.height
}
func (self *AvlNode) Size() int {
if self == nil {
return 0
}
return 1 + self.left.Size() + self.right.Size()
}
func (self *AvlNode) Has(key Hashable) (has bool) {
if self == nil {
return false
}
if self.key.Equals(key) {
return true
} else if key.Less(self.key) {
return self.left.Has(key)
} else {
return self.right.Has(key)
}
}
func (self *AvlNode) Get(key Hashable)(value interface{}, err error){
if self == nil {
return nil, fmt.Errorf("Key '%v' was not found.", key)
}
if self.key.Equals(key) {
return self.value, nil
}else if key.Less(self.key) {
return self.left.Get(key)
}else {
return self.right.Get(key)
}
}
func (self *AvlNode) pop_node(node *AvlNode) *AvlNode {
if node == nil {
panic("node can't be nil")
} else if node.left != nil && node.right != nil {
panic("节点不能同时具有left和right")
}
if self == nil {
return nil
}else if self == node {
var n *AvlNode
if node.left != nil {
n = node.left
}else if node.right != nil {
n = node.right
}else{
n = nil
}
node.left = nil
node.right = nil
return n;
}else{
if node.key.Less(self.key) {
self.left = self.left.pop_node(node)
}else {
self.right = self.right.pop_node(node)
}
self.height = max(self.left.Height(), self.right.Height()) + 1
return self
}
}
func (self *AvlNode) push_node(node *AvlNode) *AvlNode {
if node == nil {
panic("node can't be nil")
} else if node.left != nil || node.right != nil {
panic("node只能作为叶子节点")
}
if self == nil {
node.height = 1
return node
}else{
if node.key.Less(self.key) {
self.left = self.left.push_node(node)
}else{
self.right = self.right.push_node(node)
}
self.height = max(self.left.Height(), self.right.Height()) + 1
return self
}
}
func (self *AvlNode) _md(side func(*AvlNode) *AvlNode) *AvlNode {
if self == nil {
return nil
} else if side(self) != nil {
return side(self)._md(side)
} else {
return self
}
}
// 一直往左边走,直到找到最下面的节点(该节点没有左孩子),返回返回这个节点
func (self *AvlNode) lmd() *AvlNode {
return self._md(
func(node *AvlNode) *AvlNode {
return node.left
})
}
// 一直往右边走,直到找到最下面的节点(该节点没有右孩子),返回返回这个节点
func (self *AvlNode) rmd() *AvlNode {
return self._md(
func(node *AvlNode) *AvlNode {
return node.right
})
}
func (self *AvlNode) rotate_right() *AvlNode {
if self == nil {
return self
}
if self.left == nil {
return self
}
new_root := self.left.rmd()
self = self.pop_node(new_root)
new_root.left = self.left
new_root.right = self.right
self.left = nil
self.right = nil
return new_root.push_node(self)
}
func (self *AvlNode) rotate_left() *AvlNode {
if self == nil {
return self
}
if self.right == nil {
return self
}
new_root := self.right.lmd()
self = self.pop_node(new_root)
new_root.left = self.left
new_root.right = self.right
self.left = nil
self.right = nil
return new_root.push_node(self)
}
func (self *AvlNode) balance() *AvlNode {
if self == nil {
return self
}
for abs(self.left.Height()-self.right.Height()) > 2 {
if self.left.Height() > self.right.Height() {
self = self.rotate_right()
} else {
self = self.rotate_left()
}
}
return self
}
// 即使是self为nil,只要它是*AvlNode,就可以调用Put函数
func (self *AvlNode) Put(key Hashable, value interface{}) (_ *AvlNode, updated bool) {
if self == nil {
return &AvlNode{key: key, value: value, height: 1}, false
}
if self.key.Equals(key) {
self.value = value
return self, true
}
if key.Less(self.key) {
self.left, updated = self.left.Put(key, value)
} else {
self.right, updated = self.right.Put(key, value)
}
if !updated {
//-----------------------------
return self.balance(), updated
}
return self, updated
}
immutable AVL tree.
interface.go
type Entry interface {
Compare(entry Entry)int
}
type Entries []Entry
mock_test.go
type mockEntry int
func (me mockEntry)Compare(other Entry) int {
otherMe := other.(mockEntry)
if me > otherMe {
return 1
}
if me < otherMe {
return -1
}
return 0
}
node.go
package main
type node struct {
balance int8 // bounded, |balance| should be <= 1
children [2]*node
entry Entry
}
// copy返回此节点的副本,其中包含指向原始子节点的指针
func (n *node) copy() *node {
return &node{
balance: n.balance,
children: [2]*node{n.children[0], n.children[1]},
entry: n.entry,
}
}
//newNode为提供的条目返回一个新节点。nil条目用于表示虚拟节点。
func newNode(entry Entry) *node {
return &node{
entry: entry,
children: [2]*node{},
}
}
node_test.go
import (
"github.com/stretchr/testify/assert"
"testing"
)
func TestNode(t *testing.T) {
node1 := newNode(mockEntry(1))
node1.children[0] = newNode(mockEntry(1))
node1.children[1] = newNode(mockEntry(2))
// node1和node2所代表的内存地址不同,但是指向相同的孩子内存
node2 := node1.copy()
assert.Equal(t, &node1.children[0], &node2.children[0])
}
avl.go
// Immutable树通过复制分支来实现
type Immutable struct {
root *node
number uint64
dummy node // helper for inserts.
}
func (immutable *Immutable) init() {
immutable.dummy = node{
children: [2]*node{},
}
}
func NewImmutable() *Immutable {
immutable := &Immutable{}
immutable.init()
return immutable
}
https://www.cnblogs.com/54chensongxia/p/11575467.html
https://my.oschina.net/u/4543837/blog/4382955
https://www.sohu.com/a/270452030_478315
https://blog.csdn.net/xiaojin21cen/article/details/97602146
https://blog.csdn.net/qq_25343557/article/details/89110319
https://blog.csdn.net/weixin_36888577/article/details/87211314
https://www.cnblogs.com/yichunguo/p/12040456.html