一文带你读懂排序算法(五):快速排序算法
![]()
点击上方蓝字关注我们
![]()
快速排序算法是一种非常高效的排序算法,它采用“分而治之”的思想,将大的拆分为小的,小的拆分为更小的。
如果说,希尔排序是直接插入排序的升级(插入类),堆排序是简单选择排序的升级(选择类),那么快速排序等于前面我们认为最慢的冒泡排序的升级(交换类)。
快速排序算法是图灵获奖者Tony Hoare 设计出来的,他在形式化方法理论以及ALGOL60 编程语言发明中有卓越的贡献,是上世纪最伟大的计算机科学家之一。而快速排序算法只是他众多贡献中的一个小发明而已。
其原理如下:对于一组给定的记录,通过一趟排序后,将原序列分为两部分,其中前一部分的记录均比后一部分的所有记录小(有序);然后再依次对前后两部分的记录进行快速排序,递归该过程,直到序列的所有记录均有序为止。
![]()
图解快排算法思想
结合图例,快速排序的算法步骤大致如下:
-
1、我们有一个数组:[2, 1, 7, 9, 5, 8]
-
2、分割1:按照快速排序的思想,首先把数组筛选成较小和较大的两个子数组。
选择基准值7,将原数组分割为两个子数组:[2,1,5] 和 [7,9,8]
-
3、分割2:针对两个子数组:[2,1,5] 和 [7,9,8],在较小的子数组里选 2 作为基准值,在较大的子数组里选 8 作为基准值,继续分割子数组。
基准值2,[2,1,5] 分割为:[1] 和 [2,5]
基准值8,[9,8] 分割为:[8] 和 [9]
-
4、分割3:继续将元素个数大于 1 的子数组进行划分,当所有子数组里的元素个数都为 1 的时候,原始数组也被排好序了。
基准值2,[2,5] 分割为:[2] 和 [5]
基准值8,[9,8] 分割为:[8] 和 [9]
-
5、分割结果,所有子数组的元素个数都为1,得到结果数组:
-
我们从上面可以总结出规律,在实行分治过程中,如何选择基准值并拆分数组是难点。
拆分算法是整个快速排序中的核心,快速排序拥有非常多的拆分方式,其中广泛使用的是单指针遍历法与双指针遍历法。篇幅所限,我们这里对面试常常问的双指针遍历算法进行图解剖析。
![]()
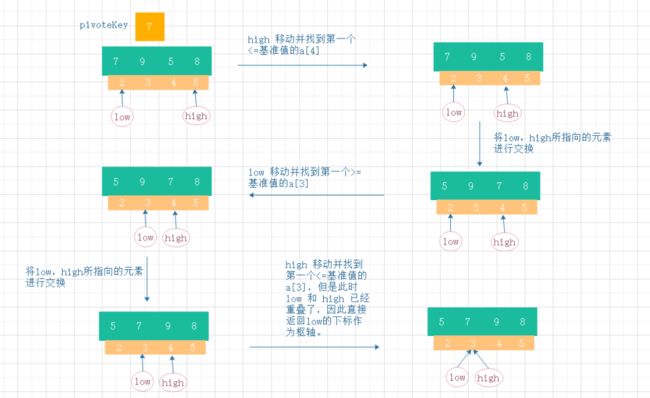
快速排序算法之双指针遍历实现图解
快速排序算法之双指针遍历实现图解:
1、首先,我们得到一个初始数组:[2,1,7,9,5,8]
2、进行第1次枢轴挑选,得到枢轴元素下标=1
3、根据第1次枢轴挑选结果,进行递归处理
4、递归1:左边数组
5、递归1:右边数组
6、进行第2次枢轴挑选,得到枢轴元素下标=3
7、根据第2次枢轴挑选结果,进行递归处理
8、递归2:右边数组
9、递归2:左边数组
10、进行第3次枢轴挑选,得到枢轴元素下标=5
11、此时,我们完成对数组的快速排序,得到顺序数组输出:[1, 2, 5, 7, 8, 9]
![]()
![]()
快速排序算法之双指针遍历实现代码
下面是快速排序的算法实现:
public class QuickSort { public static void main(String[] args) { int[] array = {2, 1, 7, 9, 5, 8}; QSort(array, 0, 5); System.out.println(Arrays.toString(array)); } private static void QSort(int[] nums, int low, int high){ int pivot; if (low >= high){ return; } // 难点也是核心,partition函数工作内容:选取某个中枢元素(枢轴,pivot),然后想办法将它放到某一位置, // 使得它左边的值都小于它,右边的值都大于它。 pivot = partition(nums, low, high); //分解为更小的问题,递归 QSort(nums, low, pivot -1); QSort(nums, pivot+1, high); } /** *
* 1、交换顺序表nums的记录,使得枢轴到位,并返回所在位置 * 2、确保枢轴左边元素<枢轴,枢轴右边元素>枢轴 * 3、选取枢轴策略就是元素的中位数的下标。 */ private static int partition(int[] nums, int low, int high) { int pivotKey = nums[low]; while (low < high){ while (low < high && nums[high] >= pivotKey){ //find out the element which is smaller then pivotKey high --; } //一次遍历,找到比基准值更小的元素并排序到前面 swap(nums, low, high); while (low < high && nums[low] <= pivotKey){ //find out the element which is bigger then pivotKey low++; } //一次遍历,找到比基准值更大的元素并排序到后面 swap(nums, low, high); } return low; } static void swap(int[] nums, int i, int j){ int tmp = nums[i]; nums[i] = nums[j]; nums[j] = tmp; } }
输出:
[1, 2, 5, 7, 8, 9]
![]()
![]()
快排复杂度分析
我们来分析下快速排序算法的性能:
快速排序的时间复杂度取决于快速排序递归的深度,
-
在最优情况下,快速排序算法的时间复杂度为 O (nlogn)。
-
在最坏情况下,待排序序列为正序或者逆序,每次划分只得到一个比上次少一个记录的子序列(另一个为空),最终时间复杂度为O(n^2)。
-
由数学归纳法,其数量级为 O(nlogn)。
快速排序的空间复杂度主要是递归造成的栈空间的使用,
-
最好情况,递归树的深度为 logn,那么它的空间复杂度也是O(logn)。
-
最坏情况,要进行 n-1 次递归调用,那么空间复杂度就是 O(n)。
-
平均情况,空间复杂度为 O(logn)。
由于关键字的比较和交换是跳跃进行的,因此快速排序是不稳定的排序方法。
![]()
总结
递归排序算法,还是有不少值得优化的地方:
1、优化选取枢轴:
采用三数取中法(median-of-three),即取是哪个关键字先进行排序,将中间数作为枢轴,一般使用左端、右端和中间三个数,或者随机选取。
或者采用九数取中(medina-of-nine),从数组中三次取样每次三个,基于样品取中数,然后从三个中数再取中数作为枢轴。
2、优化不必要的交换
3、优化小数组时的排序方案
如果数组非常小,快速排序反而不如直接插入排序
直接插入排序算法是简单排序算法中性能最好的
一枚少年郎,公众号:后台技术汇一文带你读懂排序算法(一):冒泡 & 快速选择排序 & 简单插入排序算法
原因在快速排序用到了递归操作,大量数据排序时,这点性能影响是可以忽略的。但只有几个记录要排序时,就是一个大炮打蚊子的问题了。
4、优化递归操作
递归对性能是有影响的,栈的每次调用都是会耗费资源。如果可以减少递归,会大大提高性能。
![]()
—END—
扫描二维码
获取技术干货
后台技术汇
![]()
点个“在看”表示朕
已阅