数据结构—排序算法2（归并排序与快速排序）

排序算法

5 归并排序

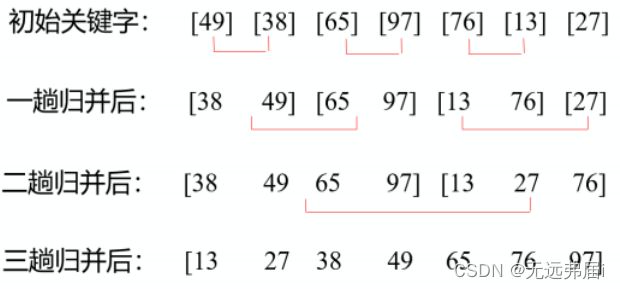
• 思路：将初始序列的n个数据看作n个有序的子序列，每个子序列的长度为1，然后两两归并，得到n/2个长度为2或者1的有序子序列；接着再两两合并……，直到得到长度为n的有序序列为止，因此，也称2-路归并排序，如下：

• 空间复杂度O(n)

• 时间复杂度O(nlogn)：一趟归并遍历n个数据，由完全二叉树的深度可知，需要进行log2n次

• 代码实现（非递归，稳定）：

//gap--两两归并---两个归并段----每个归并段元素最大数量gap
void Merge(int* arr, int len, int gap,int* tmp) {

	int left1 = 0;
	int right1 = left1 + gap-1;
	int left2 = right1 + 1;
	int right2 = left2 + gap - 1 <= len - 1 ? left2 + gap - 1 : len - 1;

	int i = 0;//i遍历tmp
	//足够两个归并段
	while (left2 < len) {
		//一组归并段
		while (left1 <= right1 && left2 <= right2) {
			//谁小谁下来 ++
			if (arr[left1] <= arr[left2]) {
				tmp[i++] = arr[left1++];
			}
			else {
				tmp[i++] = arr[left2++];
			}
		}

		if (left1 > right1) {//拷贝第二个归并段到tmp
			for (int j = left2; j <= right2; j++) {
				tmp[i++] = arr[j];
			}
		}
		else {//拷贝第一个归并段到tmp
			for (int j = left1; j <= right1; j++) {
				tmp[i++] = arr[j];
			}
		}
		left1 = right2 + 1;
		right1 = left1 + gap - 1;
		left2 = right1 + 1;
		right2 = left2 + gap - 1 <= len - 1 ? left2 + gap - 1 : len - 1;

	}

	//不足两个归并段     Left1~Right1有数据
	for (int j = left1; j < len ; j++) {
		tmp[i++] = arr[j];
	}
	//将tmp拷贝给arr
	memcpy(arr, tmp, sizeof(int)*len);//string.h

}

void MergeSort(int* arr, int len) {
	int* tmp = (int*)malloc(sizeof(int) * len);
	assert(tmp != NULL);
	for (int i = 1; i < len; i *=2) {
		Merge(arr, len, i,tmp);
	}
	free(tmp);
	tmp = NULL;
}

6 快速排序

• 思路：每一次排序，让left和right指向序列的最左边和最右边，将left的值作为基准放入tmp中，以right–从右往左找到比基准小的值，放入左边空位，以left++从左往右找到比基准大的值，放入右边空位，直到left=right时，将基准tmp的值放入此处。此时，以基准为分界线，序列分为两部分，左边的值都小于基准，右边的值都大于基准。
• 整个快速排序的过程可递归进行，若待排序序列中只有一个记录，则已经有序，否则集训进行快速排序，如下：
  
• 空间复杂度O(logn)：递归时，需要有一个栈来存放每层递归调用时的参数（新的left，right等），最大递归调用层数与递归树的深度一致，因此，空间开销为O(log2n)
• 平均时间复杂度O(nlogn)：一层递归遍历n个数据，由完全二叉树的深度可知，需要进行log2n次
• 数据完全/趋于有序，退化成O(n^2) ；例如：1 2 3 4 5----时间复杂度为O(n^2)
• 代码实现（递归，不稳定）：

//分割函数
int Partition(int* arr,int left, int right) {
	assert(arr != NULL);
	//选取基准
	int tmp = arr[left];
	while (left < right) {
		//从右向左找，<= 基准小 向前丢
		while (left<right && arr[right] > tmp) {
			right--;
		}
		arr[left] = arr[right];
		//从左向右找，>基准大 向后丢
		while (left<right && arr[left] <= tmp) {
			left++;
		}
		arr[right] = arr[left];
	}
	arr[left] = tmp;
	return left;
}

void Quick(int* arr, int left, int right) {
	assert(arr != NULL);
	int index = Partition(arr, left, right);
	if (index - left >= 2) {
		Quick(arr, left, index-1);
	}
	if (right - index >= 2) {
		Quick(arr, index+1, right);
	}
}

void QuickSort(int* arr, int len) {
	assert(arr != NULL);
	if (len <= 1)return;
	Quick(arr, 0, len - 1);
}

快速排序的优化

• 快速排序的特点：数据越无序，效率越高，最好可以达到O(nlog2n)；数据越有序，效率越差，最差接近于O(n^2)。
• 优化方法

优化1

如果数据量过小，可以直接插入排序。因为n小，n^2也不会太大；

void QuickSort(int* arr, int len) {
	assert(arr != NULL);
	if (len <= 1)return;
	if (len <= 1000) {
		InsertSort(arr, len);
	}
	Quick(arr, 0, len - 1);
}

优化2

三数取中法，取最左端值、最右端值、中间值，三者中不大不小的作为基准值；

void Three_Num_Mid(int* arr, int left, int right) {
	int mid = (left + right) / 2;
	//将左边和中间位置de较大值放在中间
	if (arr[left] > arr[mid]) {
		int tmp = arr[left];
		arr[left] = arr[mid];
		arr[mid] = tmp;
	}
	//将三个数中的最大值放在最右边
	if (arr[mid] > arr[right]) {
		int tmp = arr[mid];
		arr[mid] = arr[right];
		arr[right] = tmp;
	}
	//不大不小的值，在左边或者中间，如果在中间，则放到最左边
	if (arr[left] < arr[mid]) {
		int tmp = arr[left];
		arr[left] = arr[mid];
		arr[mid] = tmp;
	}
}
void Quick(int* arr, int left, int right) {
	assert(arr != NULL);
	Three_Num_Mid(arr, left, right);
	int index = Partition(arr, left, right);
	if (index - left >= 2) {
		Quick(arr, left, index-1);
	}
	if (right - index >= 2) {
		Quick(arr, index+1, right);
	}
}

void QuickSort(int* arr, int len) {
	assert(arr != NULL);
	if (len <= 1)return;
	Quick(arr, 0, len - 1);
}

优化3

随机数法，通过使用随机数，将数据打乱；

优化4

递归时，如果子序列数据量过小，也可以直接调用直接插入排序。