C数据结构：树和森林存储方式与遍历方式

树的存储方式

树的定义：只有一个根节点，但是分支可以没有规律，也就是说不像二叉树那样每个结点最多生出两个分支。
而且树和接下去学习的图都有一个共同的特点就是套娃，无限套娃。

树的存储结构方式都会用到数组顺序存储结构，数组是核心，数组结合链式的也有。
至于为什么树要用到数组比较多，我认为是数组有一个很好的点就是他的位置可以很容易且快速的找到并访问，但是链式就不具有该优点，因为链式是一条绳子上的蚂蚱，必须一个一个的找。

---

双亲表示法

很显然就像名字说的那样，用该结点的双亲结点位置来表示当前的结点。
双亲表示法就比如：让孩子记住自己父母的电话一样，孩子找到父母就很容易。但是反过来，当父母去找很多孩子的其中一个的电话的时候就很麻烦，要一个一个的去找，因为他们的父母也和孩子们一样，也是有爸妈的，也只是特别的记录了自己父母的电话。

反观回来我们存储方式中，双亲表示法是用顺序存储结构，每一个结构体里面包含着两个域，一个数据域，另一个就是双亲结点的位置域。
结点结构代码如下：

typedef struct Ch{
	ElemType date;//数据域
	int parent;//父母域
}PTNode;

因为我们用的是数组顺序存储结构，所以父母域是int类型，表示他的他的双亲结点的位置在哪，也就是说方便他找回自己的父母。

树的结构代码如下：
结合上面的结点结构

//数组里面的空间表示这棵树的最大容量，并不是这棵树现在具有的结点数。
#define MAX_TREE_SIZE 100
typedef struct Tree{
	PTNode nodes[MAX_TREE_SIZE];
	int r, n;//r 是根节点的位置， n 这里才是表示是树中总结点的个数
};

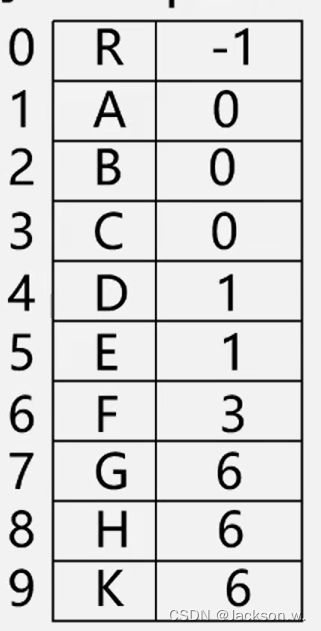
树的数组效果呈现如下图所示：

（因为根节点没有双亲结点，就用-1表示）
[↓下标 ] [ ↓数据域 ] [ ↓双亲结点下标 ]

妙处： 再用一个结构体作为树的结构体，包含着孩子结点结构体数组就可以明了的表示出一棵树。（方便理解森林）
↑ 解释：树中的分支结点都可以存在数组中，只要我们知道他的父母结点就可以画出该树的结构是怎样的，再返回去说就是双亲表示法表示了一棵树。
也就是说，当我们知道了一个双亲表示出来的数组，我们就可以通过找相同的双亲结点，这些双亲结点相同的就是同一个妈生，如此一来就可以画出我们的树的结构了。

注意的点：每一个结点都要有一个空间表示出来，也就是说结点数有几个，数组都要把这些结点存下来，我刚开始犯错误就是误以为只要存了父母结点位置就可以找到了，这么二壁的想法可能也就只有我能犯 。

细想一下：我们找该结点的孩子就是要去找到谁的双亲结点存的是该结点的下标位置，只需要遍历一下父母域就可以，相同父母域就是同一个妈生，但是当数据量很大的时候就变得非常的困难，因为有时候找的不是所有的孩子，而是某个指定的孩子，这时候不仅要找父母域还要对比数据域是否为我们要找的孩子。

优点：找父母容易。
缺点：找孩子难（其实是麻烦，也能找到）。

---

孩子链表表示法

顾名思义就是用每一个孩子作成链表，而且还是要同一个双亲结点的孩子才能做成一个链表。
我的理解：同一个妈生的孩子，第一个出生的孩子作为老大，也就是链表的头，然后连成一线做成链表，这样如此一来，每一个父母只需要通过老大结点就能找到所有的孩子结点。如果没有孩子的话，把他的头指针域置为空就行。可以想象成父母结点是一个箱子，箱子里面放的都是这个父母的孩子，只不过孩子们排起了队而已。

孩子链表结构体代码如下：

typedef struct _Ch{
	ElemType date;//数据域
	struct Ch* next;//孩子链表指针域
}Ch;

双亲结点（父母）结构体代码如下：

typedef struct _PTBox{
	ElemType date;//父母自己的数据域
	struct Ch* firstchild;//存着第一个孩子的结点指针域
}PTBox;

树的结构体代码如下：

//数组里面的空间表示这棵树的最大容量，并不是这棵树现在具有的结点数。
#define MAX_TREE_SIZE 100
typedef struct Tree{
	struct PTBox nodes[MAX_TREE_SIZE];
	int r, n;//r 代表根节点， n 这里才是表示是树中总结点的个数
};

孩子链表表示法呈现效果如下图所示：
↓下标 ↓数据域 ↓首孩子指针 -> 孩子的next

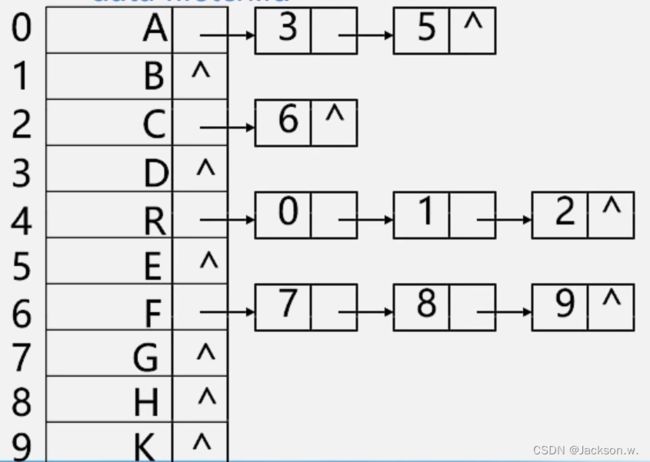
总结：孩子链表表示法分为三层，一层是孩子链表结构体，一层是双亲结点结构体，两层之间相扣着，最外层是双亲结点结构体，他包着孩子结点结构体，所以说双亲结点结构体相当于一个盒子，包含着该双亲结点所有的孩子结点在里面。再然后用每一个双亲结点结构体做成一个数组，也就是把这些双亲结点结构体包在一个盒子中，把该数组塞进一个结构体里面，那么该结构体就变成了一棵树。

（再次赘述一下思路↓）
记住： 树的组成部分有三块（也可以两块），一个存放孩子链表结点的结构体，另一个是双亲结点结构体，双亲结点结构体里面包含着孩子链表结构体，双亲结点结构体做成数组后就是一个树了，所以说其实两部分也可以组成一棵树，但是为了简洁明了方便后续森林的操作，我们还是把这结构体数组放在一个结构体中形成新一棵树比较好。

优点：找孩子容易
缺点：找双亲难

---

结合两个表示法：
双亲表示法和孩子链表表示法的优缺点相辅相成
由此我们可以结合起来用，让他孩子和双亲都容易找。

双亲表示法因为有双亲结点的下标才说容易找到双亲，那我们在孩子链表表示法里面的双亲结点多加一个存放该双亲结点的双亲结点（套娃…）。

我愿称之为家庭版表示法
修改一下孩子链表表示法里面的双亲结点结构体代码即可，修改如下：

typedef struct _PTBox{
	ElemType date;//父母自己的数据域
	int index;//父母自己的父母的下标位置
	struct Ch* firstchild;//存着第一个孩子的结点指针域
}PTBox;

如此一来，家庭版表示法虽然消耗了空间，但是也变得很容易找到各个结点之间的关系了。

我细想了一下：这两个都有一个规律，那就是把谁做成一个数组的规律。
$\Downarrow$$\Downarrow$$\Downarrow$$\Downarrow$$\Downarrow$$\Downarrow$$\Downarrow$$\Downarrow$
在双亲结点表示法 中，是把所有结点看成孩子结点，然后把所有孩子结点用一个数组表示出来，孩子结点里面包着他们双亲结点的下表位置，再将数组外包成一个结构体，这个结构体就是这样一一棵树。（用了两个结构体）
在孩子链表结点 中，是把所有结点看成双亲结点，然后把所有双亲结点用一个数组表示出来，双亲结点里面包含着第一个孩子的指针，然后首孩子和他的兄弟做成一个链表，然后把数组外包成一个结构体，这个结构体就是一棵树。（用了三个结构体）

---

孩子兄弟表示法（二叉树表示法）

首先这个孩子兄弟法是为后面树和二叉树转换为基础的一个表示法，
就是说如果弄懂了这个表示法其实树和二叉树转换也就易如反掌。

内心OS： 第一次听到这个名字我是很蒙圈，这和孩子链表表示法有什么区别，
学到后面，我发现这个孩子兄弟表示法更牛。
确认过眼神，是我想不出来的存储方式，被前辈们的想法大受震撼。

我的理解：左孩子，右兄弟
因为孩子兄弟表示法其实质是通过二叉树来表示出来，如果单单的用左右孩子来表示肯定是不够的的，因为树的孩子数不确定，因此前辈们想到了一个办法，就用两个指针来表示，也就是左孩子，右兄弟。

孩子兄弟表示法的结构体代码如下：

typedef struct _ChBro{
	ElemType date;
	struct _ChBro* firstchild;//左孩子
	struct _ChBro* nextBrother;//右兄弟
};

由于每次都是这种递归的形式，自己定义自己的结构体模式，所以其实每次生成一个结点都会有对应他的左孩子，右兄弟，因此就用一个二叉树表示出来了一棵没有规律的树了，妙哉妙哉。

用二叉树来表示树的效果如下图所示：

---

缺点：当然我们可以看到这个表示法也有一个缺点，就是找结点的双亲结点比较困难。
解决办法：我们可以在结点结构体中再增加一个指向他的双亲结点的指针域。（没有什么是加一层解决不了的，有那就再加）

缺点解决办法的代码如下：

typedef struct _ChBro{
	ElemType date;
	struct _ChBro* parent;//双亲结点指针
	struct _ChBro* firstchild;//左孩子
	struct _ChBro* nextBrother;//右兄弟
};

---

树和二叉树的转换

当初我学到这里的时候其实已经大概明白是怎么个转换法了，因为在孩子兄弟表示法中已经学了如何让一棵树用二叉树表示出来。

二叉树 转换成 树
我总结了以下几点：

• 拿到二叉树想转为树的时候，要时刻记住左孩子右兄弟。
• 二叉树的根结点的左分支是他的左边第一个孩子。
• 如果有右分支就代表该分支是根节点的第二个孩子的结点，同时也是左分支的兄弟结点。
• 把左分支和右分支还有右分支的右分支还有右分支的右分支的右分支…的这一条线上的结点都和根结点连上，然后把这一条线全部拆掉。
• 只要把递归思想和记住了每个结点上都是左孩子右兄弟就可以很容易转换出来。
  
  树 转换成 二叉树
  我总结了以下几点：
• 拿到一棵树的图后，根节点的左边第一个孩子作为二叉树的左分支。
• 根节点除了左边第一个孩子，该根节点如果还有剩下的孩子结点，就把这些结点用左分支连在一起，形成一条以左分支为根结点，该左分支的右孩子为他的兄弟们。
• 如果根节点左边第一个孩子也有属于他的孩子，那么把他作为一个新的根节点，重复上述操作即可。
  

森林和二叉树的转换

森林的定义：
森林就是多棵树组成的一个集合
森林具有多个树根
（就很常识性的的内容了）

森林转为二叉树
总结了以下几点：

• 首先是把左边第一棵树的根结点作为二叉树的根结点，别问必须这样做，因为二叉树是有原则的一个东西。
• 其次，按照每一棵树转化为二叉树的做法一样
• 把每一棵树的根结点连在第一棵树的根节点的右孩子作为他的孩子部分

二叉树转化为森林
总结了以下几点：

• 二叉树的根结点作为第一棵树的根结点
• 连接二叉树根结点的右孩子的那一条线下去，把所有结点都切开
  类似于这样↓
  
• 上面执行完成后就是变成了好几个二叉树了，这时候按照二叉树转换成树的方式变成一棵棵树就可以了。

树和森林的遍历

树的遍历方式

• 先根遍历：若树不为空，则先访问根结点，然后依次先根遍历各棵子树。这和二叉树的先序遍历思想一模一样，就是多了几个孩子结点。
• 后根遍历：若树不为空，则先依次后根遍历各棵子树，然后访问根结点。这和二叉树的后序遍历思想也一模一样，也无非是多了几个孩子结点而已。
• 层次遍历：若树不为空，则至上而下，从左至右访问树中每一个结点。这和二叉树的层次遍历思想也一模一样，同样需要用到队列的思想，进行入队出队，不过入队多了几个小孩子结点排队罢了。
• 先根后根和先序后序名字没有分别，因为树有很多根，习惯性的把树遍历叫成根遍历。

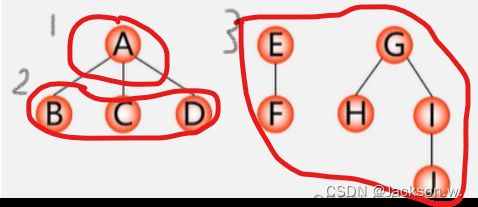
用下图进行先后根和层次遍历

先根遍历结果：ABCDE
后根遍历结果：BDCEA
层次遍历结果：ABCED

---

森林的遍历方式

因为森林有多个根，遍历之前需要把他分一下块，也就是说需要分成三部分
第一部分：第一棵树的根作为一部分
第二部分：第一棵树中除了根之外所有的结点为第二部分
第三部分：除了第一棵树剩下的树为第三部分
（这里你可以像我一样想象成二叉树，第一部分是根，第二部分是左孩子，第三部分是右孩子，这样就有了下面的先序和中序遍历）

两种遍历方式

• 先序遍历：先序的意思是在三部分中，先序遍历第一部分然后遍历第二部分，再跟着第三部分。
• 中序遍历：中序的意思是三部分中，先遍历第二部分然后遍历第一部分，再跟着第三部分。

用下图的森林进行先序和中序遍历：

先序遍历结果：ABCDEFGHIJ
中序遍历结果：BCDAFEHJIG

浅谈一下几个问题

为什么树没有中根遍历？

我的理解：树如果按照中跟遍历的方法遍历的话，顺序应该是怎样的我们无从的知，因为之前二叉树的中序遍历是左根右，现在树有这么多个孩子，已经不能说哪个是左中右了，只有先后。所以硬要说为什么没有中根遍历的话，就是中根遍历没有确定的遍历顺序。

另一种解释方式：当你把树转化为二叉树的时候我们找不到一个中序（中根）遍历结果能和你的树中根遍历能对应。

为什么森林没有后序遍历？

我的硬核解释：森林为啥有中序却没有后序，先说一下森林为什么会有先序和中序遍历，这个名字和二叉树的先序中序遍历一模一样，当然科学是严谨的，所以一样的名字对应着森林中使用先序中序遍历和在这个森林转换成二叉树的时候使用先序中序遍历结果是一样的，但是同样的我们始终找不到一个森林的后序遍历和森林转化为二叉树后的后序遍历对应。

另一种解释方式：当我们把森林转化为二叉树的时候，第一棵树的根结点必然为二叉树的根结点，二叉树使用后序遍历必然根结点放在整个遍历的最后面才结束遍历，但是如果你在森林就实行后序遍历，当你第一棵树使用了后序遍历，你的第一个棵树的根只是在第一棵树遍历的后面结束，但是森林不止一棵树，还有好多，所以该根结点就和你森林转换为二叉树的根节点遍历的顺序不对应了。
（就像生活一样，先来后到的顺序有时候很重要，你是森林的时候没有唯一确定的后序遍历，但是你变为二叉树的时候就有了）

实质：
森林的中序遍历其实是每一个棵树的后根遍历
每一棵树的后根遍历其实是二叉树的中序遍历

总结

二叉树：先、中、后序遍历
树：先、后序遍历。
森林：先、中序遍历。
（尽量理解是最好的）

归根结底，我们树和森林之所以有这些特定的名字的遍历方式都是得益于二叉树，
记住，二叉树的三种遍历方式是唯一的。
因为这些遍历方式的结果能与之把树、森林转化为二叉树之后的遍历结果唯一对上。
A：树有多个根，遍历结果不唯一，但是我们为了唯一性，
首先把树转化为二叉树，所以树只能有先序遍历和后序遍历。
B：因为森林有多个树，遍历结果更不唯一，但是我们为了唯一性，
首先把森林转化为二叉树，所以森林只能有先序遍历和中序遍历。

注明：本博客的截图均来自B站王卓老师的数据结构的PPT。