【机器学习】带你轻松理解什么是强化学习中的贝尔曼方程
系列文章目录
第十八章 Python 机器学习入门之强化学习
目录
系列文章目录
前言
一、什么是贝尔曼方程
二、贝尔曼方程为什么有用
三、贝尔曼方程是怎么来的
总结
前言
贝尔曼方程是强化学习中最重要的一个方程式。如果可以计算状态S 的状态动作函数 Q(s,a),那么它为我们提供了一种从每个场景中选择一个好的动作的方法。只需选择动作A,它会为什么提供Q(s,a) 的最大值。现在的问题是,如何计算Q(s,a)?在强化学习中,有一个称为贝尔曼方程(bellman equation) 可以帮助我们计算状态动作函数Q。
一、什么是贝尔曼方程
贝尔曼方程是强化学习中最重要的一个方程式。
如果可以计算状态S 的状态动作函数 Q(s,a),那么它为我们提供了一种从每个场景中选择一个好的动作的方法。只需选择动作A,它会提供Q(s,a) 的最大值。
现在的问题是,如何计算Q(s,a)?
在强化学习中,有一个称为贝尔曼方程(bellman equation) 可以帮助我们计算状态动作函数Q。
下面我们来看看什么是贝尔曼方程bellman equation
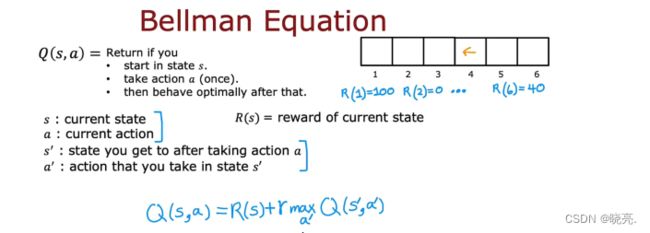
我们使用s表示当前状态,R(s) 表示当前状态的奖励,对于我们的马尔科夫决策的例子,R(1)=100,R(2)=0,,,R(6)=40。
我们使用a 表示当前的动作,
使用s'表示采取该行动后所达到的状态
使用a’表示在状态s’下,可能采取的行动
使用上面定义的元素,我们可以得到贝尔曼方程,如图
二、贝尔曼方程为什么有用
让我们来看几个例子,看看为什么这个方程有用。
来看看状态2 的Q 和动作A,将贝尔曼方程应用于此,看看它给我们带来了什么价值。
如果当前状态S是状态2,并且动作A 是向右运行,采取该行动后所达到的状态s'=3,
这时候应用贝尔曼方程,带入公式,如图,确保Q(s', a')最大,所以下一步会向左运行,最后的结果为12.5.
如果当前状态S是状态4,并且动作A 是向左运行,采取该行动后所达到的状态s'=3,
这时候应用贝尔曼方程,带入公式,如图,确保Q(s', a')最大,所以下一步会向左运行,最后的结果为12.5.
如果我们处于终端状态,则贝尔曼方程会简化为 Q(s,a)=R(S)
三、贝尔曼方程是怎么来的
回顾一下状态动作函数Q的定义:如果你从某个状态 S 开始,并只采取行动 A 一次, 在采取行动 A 一次之后,你就会表现得最佳。
我们知道,任何状态S 的最佳可能回报是Q(s,a) 上的最大值,
同样,对于任何状态S ' 的最佳可能回报是Q(s',a') 上的最大值
联系贝尔曼方程,如果从状态s开始,我们将采取行动a,然后采取最佳行动,
然后我们会看到,随着时间的推移,一些奖励序列。特别的是,回报将从第一步的奖励中计算出来,
一直加到终端状态。
贝尔曼方程所说的是这个奖励序列,折扣因子是什么,这个可以分解成两个组成部分。
第一部分是R(S) 是我们马上得到的奖励,也被叫做即时奖励,也就是我们从某个状态开始获得的奖励;
第二部分是在我们从状态s 开始并采取行动a之后,我们会得到一些新的状态s',Q(s',a')的定义就是假设我们将在此后表现最佳,在我们达到状态s' 后,我们将表现出最佳状态 并得到 状态的最佳回报。
其中max Q(s',a')就是从最优行动a' 中得到的回报,从状态s' 开始。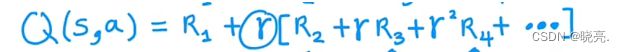
将上面的等式变化一下,我们就可以得到贝尔曼方程是怎么来的了。 
总结
总结一下,我们得到的总回报,在强化学习问题中有两个部分,第一部分是我们马上得到的奖励,然后第二部分是gamma γ 乘以我们从下一个状态开始获得的回报 Q(s',a')。这两部分组合在一起,即得到总回报,这就是贝尔曼方程的本质。
活动地址:CSDN21天学习挑战赛