如何估计池塘里鱼的数目,周边有多少车辆?
如何估计池塘里鱼的数目?
老李想估计一下自己池塘里鱼的数量,第一天他捕捞了50条鱼做好标记,然后全放回池塘。过了几天带标记的鱼完全混合于鱼群中,他又去捕捞了168条,发现做标记的鱼有8条。帮老李估算一下池塘里的鱼有多少条。
这是一个典型的用抽样样本来估计总体的统计办法。168条鱼中有8条标记鱼,这样老李可以估计标记鱼占全体鱼的比是8:168。由于总共有50条标记鱼,那么全体鱼的数目就应该是1050。
50×168÷8=1050
简单估计池塘里的鱼群的数目容易产生较大的误差,如果偶然只捞了两条标记鱼,那么池塘里鱼的总数就会被高估,50×168÷6=1400条!这样很轻易就造成了25%的误差。
减少误差的方法
基于这个原因,如果这些鱼经得起折腾的话,更好的办法是放回去再多捕捞几次,取个平均值。
先从池塘中捞出100条鱼分别做上记号,放回池塘,等鱼完全混合后,第一次捞出100条鱼,其中有4条带标记的鱼,第二次又捞出100条鱼,其中有6条带标记的鱼。 100 x = 4 + 6 100 + 100 \frac{100} {x}=\frac{4+6}{100+100} x100=100+1004+6,则, x = 2000 x=2000 x=2000。
正态分布近似估算
这是一种基于二项分布理论的方法,但在这里可用正态分布近似估算。计算误差时,只需改变样本方差的算法即可,其他都不变。以《数据化决策》书中的案例为例。
N = p ± z a 2 p ( 1 − p ) n N=p±z_{\frac{a}{2}}\sqrt{\frac{p(1-p)}{n}} N=p±z2anp(1−p)
其中:
p p p,样本比例。
z a 2 z_{\frac{a}{2}} z2a,置信区间统计量,例如95%置信区间取1.96,90%取1.645。
n n n,样本数量。
标准误差(standard error)通常是指样本统计量(如样本平均值、样本标准差等)的标准差,它反映了统计量的抽样误差。标准误差的计算公式与具体的统计量相关。
统计量的标准误差,当总体标准差未知时,可用样本标准差代替计算,这时计算的标准误差称为估计标准误差(standard error of estimation)。由于实际应用中,总体总是未知的,所计算的标准误差实际上都是估计标准误差,因此估计标准误差就简称为标准误差。同样,当总体比例的方差未知时,可用样本比例的方差代替。计算公式: p ( 1 − p ) n \sqrt{\frac{p(1-p)}{n}} np(1−p)。
先从池塘中捞出1000条鱼分别做上记号,放回池塘,等鱼完全混合后,再捞出1000条鱼,其中有50条是做过标记的,这就意味着池塘里大概有5%的鱼做过标记,因此,得出结论是池塘里大约有20000条鱼。
样本方差是用群体内的样本比例乘以非样本比例。换句话说,是将二次抓取时鱼群中做标记的比例(0.05)乘以没做标记的比例(0.95),结果是 0.05 × 0.95 = 0.0475 0.05\times0.95=0.0475 0.05×0.95=0.0475,按90%置信区间取1.645。
1.645 0.0475 1000 = 0.012 1.645\sqrt{\frac{0.0475}{1000}}=0.012 1.64510000.0475=0.012
0.05 ± 0.012 = ( 3.8 % ∼ 6.2 % ) 0.05±0.012=(3.8\% \sim6.2\%) 0.05±0.012=(3.8%∼6.2%)
因此湖中鱼的总数是16129~26316,(1000/0.062=16129,1000/0.038=26316)。
对有些人来说,这看似是一个比较大的范围,但假设我们以前的不确定性水平很高,校准估计的范围也只是2000~50000条,所以这一范围已经大为缩小了。如果我们当初放养了5000条鱼,现在仅仅是想知道鱼的总数是增加了还是减少了,那么任何大于6000的数字都表示鱼的总数增加了,超过10000条当然更好。如果把初始范围和相关阈值都考虑在内,不确定性显然已经大为减小,误差也在可接受范围之内。实际上,我们完全可以在第一次抓捕中只抓250条鱼,然后放掉,再抓250条,也就是说抽样量只有前面的1/4。假设做过标记的鱼在第2次重抓时所占比例也是5%左右,那么我们对鱼的总数超过6000条仍然很有信心,也就是说6000仍然在90%置信区间内。
这种通过抽样来揭示全貌的方法特别有用,这种方法已经用于评估美国人口普查局统计遗漏的人数、亚马孙流域未经发现的蝴蝶种类及未知的潜在顾客数量等问题。未能看到整体全貌,并不意味着不能对它进行量化。
从本质上说,抓与重抓是两次独立抽样,比较两次抽样的重合程度,可以估计群体总数。
周边有多少车辆应用思考?
如果我们想知道我们生活的区域周边有多少车辆,可否使用这样方案。
例如,我们在纵向的街道上,通过随机录像、拍照记录1000辆车牌号,下周大致相同时间,再随机记录1000辆车牌号;同样方法在横向街道,再进行一次,这样估算反映了什么呢?
反映出这个街道上,周边能到此街道的车辆规模,是这样吗?
怎么抽样更准?
抽样占比为5%,样本数分别为100、1000、1000,则整体估计情况如下:

重复抽样标记比例提高到10%,其他不变则整体估计情况如下:
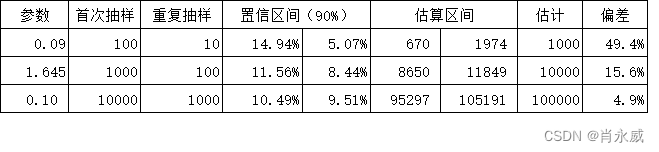
怎么抽样更准?
首先是增大样本数,其次,在样本数不变的情况下,尽量提高标记比例。
参考:
Douglas W. Hubbard. 数据化决策. 广东人民出版社. 2018.05
