第八章 排序（下）【外部排序】
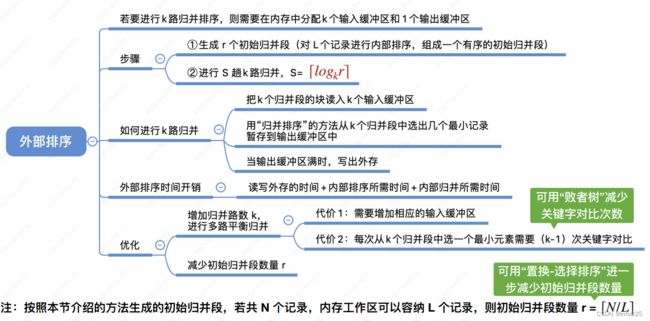
1. 外部排序
1.1 外存、内存之间的数据交换
操作系统以“块”为单位对磁盘存储空间进⾏管理，如：每块⼤⼩ 1KB 各个磁盘块内存放着各种各样的数据
磁盘的读/写以“块”为单位 数据读⼊内存后才能被修改 修改完了还要写回磁盘
外部排序：对大文件进行排序时，因为文件中的记录很多、信息量庞大，无法将整个文件复制进内存中进行排序。因此需要将待排序的记录存储在外存上，排序时再把数据一部分一部分地调入内存进行排序，在排序过程中需要多次进行内存和外存之间的交换。
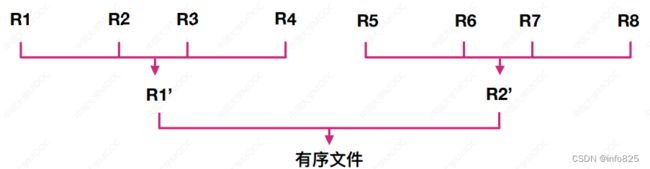
使⽤“归并排序”的⽅法，最少只需在内存 中分配3块⼤⼩的缓冲区即可对任意⼀个⼤ ⽂件进⾏排序
归并排序”要求各个⼦序列有序，每次读⼊ 两个块的内容，进⾏内部排序后写回磁盘
1.2 外部排序的步骤：
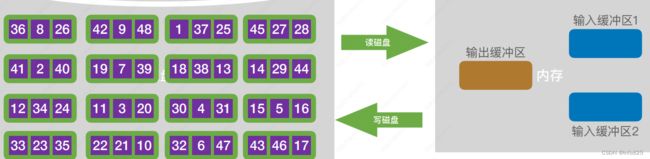
① 跟据内存缓冲区大小，将外存上的文件分成 r(8) 个子文件，依次读入内存并利用内部排序方法对它们进行排序，并将排序后得到的有序子文件重新写回外存（归并段）。16个磁盘块构造初始归并段： 需要16次“读”和16次“写”
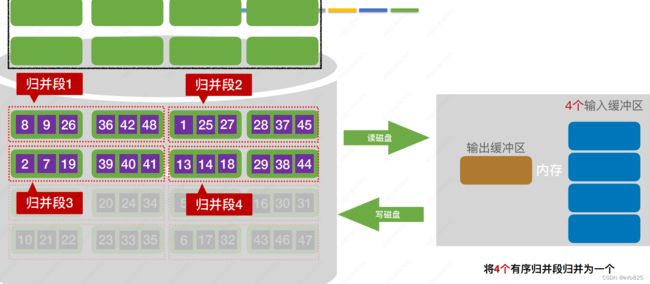
② 对这些归并段进行 S 趟 k 路归并，使归并段（有序子文件)逐渐由小到大，直至得到整个有序文件为止，(其中需要在内存中分配k个输入缓冲区和1个输出缓冲区,
）
如何进行 k 路归并：
① 把k个归并段的块读入k个输入缓冲区。
② 用“归并排序”的方法从k个归并段中选出几个最小记录暂存到输出缓冲区中，缓冲区i 空了就要⽴即⽤ 归并段i 的下⼀块补上。
③ 当输出缓冲区满时，写出外存。
时间开销分析
外部排序时间开销 = 读写外存的时间 + 内部排序所需时间＋内部归并所需时间
1.3 优化k 路归并：
①增加归并路数k，但是需要增加相应的输入缓冲区，且每次从k个归并段中选出一个最小元素需要对比 (k-1) 次。
② 减少初始归并段数量r。⽣成初始归并段的“内存⼯作区”越⼤，初始归并段越⻓,若能增加初始归并段的⻓度，则可减少初始归并段数量 r
采⽤4路归并，只需进⾏两趟归并即可 读、写磁盘次数= 32+32*2 = 96 次
重要结论：采⽤多路归并可以减少归并趟数，从⽽减少磁盘I/O(读写)次数
1.3 多路归并带来的负⾯影响：
①k路归并时，需要开辟k个输⼊缓冲 区，内存开销增加。
②每挑选⼀个关键字需要对⽐关键字 （k-1）次，内部归并所需时间增加
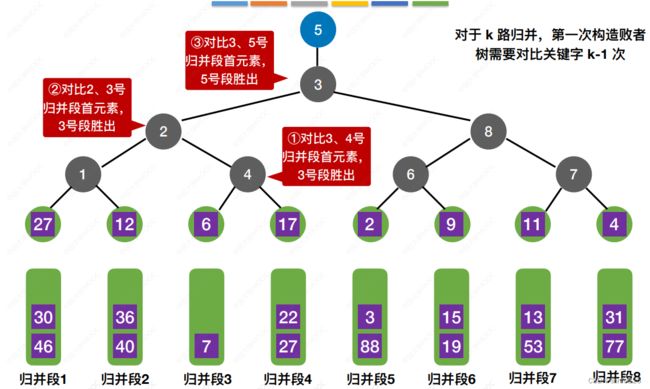
2.败者树
使⽤k路平衡归并策略，选出⼀个最⼩ 元素需要对⽐关键字 （k-1）次，导致 内部归并所需时间增加,可⽤“败者树” 进⾏优化 !
2.1 败者树解决的问题：
使⽤多路平衡归并可减少归并趟数，但是⽤⽼⼟⽅法从 k 个归并段选出⼀个最 ⼩/最⼤元素需要对⽐关键字 k-1 次，构造败者树可以使关键字对⽐次数减少到 ⌈log2k⌉
算法思想：
败者树可视为⼀棵完全⼆叉树（多了⼀个头头）。k个叶结点分别对应 k 个归并段中当前参加⽐较的 元素，⾮叶⼦结点⽤来记忆左右⼦树中的“失败者”，⽽让胜者往上继续进⾏⽐较，⼀直到根结点。
失败者留在这⼀回 合，胜利者进⼊下 ⼀回合⽐拼，最后只有⼀个冠军 在所有⽐拼中获胜，
若有8位参赛者，则构造 败者树需要 7 次⽐拼，基于已经构建好的败者树，选出 新的胜者只需进⾏ 3场⽐赛，
对于 k 路归并，第⼀次构造败者 树需要对⽐关键字 k-1 次
有了败者树，选出最⼩元素，只需对⽐关键字⌈log2k⌉次
k路归并的败者树只需要定 义⼀个⻓度为 k 的数组即可 ，叶⼦结点是 “虚拟的”
3.置换-选择排序（生成初始归并段）
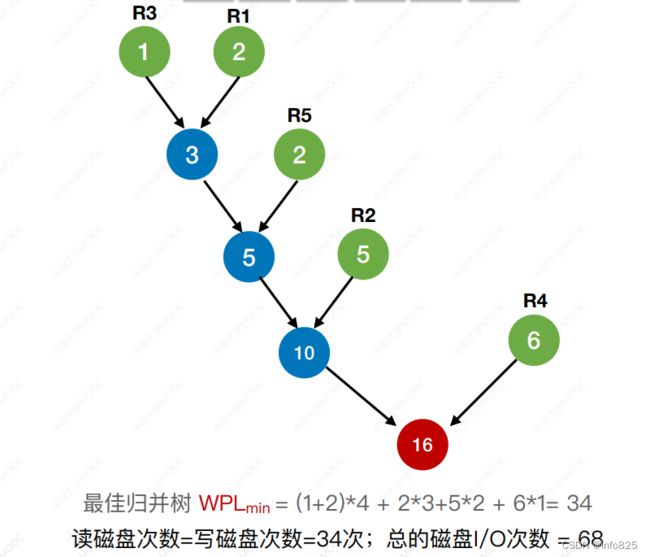
可以⽤⼀⽚更⼤的内存区域来进⾏内 部排序，⽤于内部排序的内存⼯作区WA 可容纳 l个记录，则每个 初始归并段也只能包含l 个记录，若⽂件共有n 个记录， 则初始归并段的数量 r = n/l
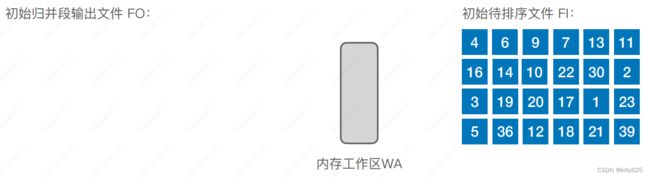
设初始待排文件为FI，初始归并段输出文件为FO，内存工作区为WA，FO和WA的初始状态为空，WA可容纳w个记录，置换-选择算法的步骤如下：
- 从FI输入w个记录到工作区WA。
- 从WA中选出其中关键字取最小值的记录，记为MINIMAX记录。
- 将MINIMAX记录输出到FO中去。
- 若FI不空，则从FI输入下一个记录到WA中。
- 从WA中所有关键字比MINIMAX记录的关键字大的记录中选出最小关键字记录，作为新的MINIMAX记录。
- 重复③~⑤，直至在WA中选不出新的MINIMAX记录为止（WA内的关键字都⽐ MINIMAX 更⼩），由此得到一个初始归并段，输出一个归并段的结束标志到FO中去。
7.重复②~⑥，直至WA为空。由此得到全部初始归并段。
使⽤置换-选择排序，可以让每个初始归并段 的⻓度超越内存⼯作区⼤⼩的限制
4. 最佳归并树
4.1 归并过程中的磁盘I/O次数
4.1.2 二路归并
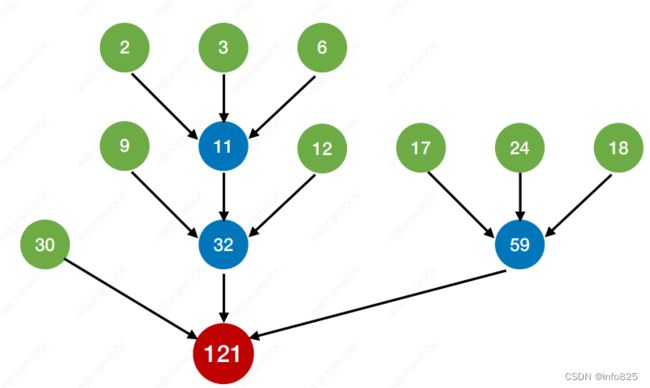
初始归并段，所占块数 各不相同，进⾏⼆路归并
每个初始归并段看作⼀个叶⼦结点，归并段的⻓度作为结点权值，则 上⾯这棵归并树的带权路径⻓度 WPL = 2*1 + (5+1+6+2) * 3 = 44
重要结论：归并过程中的磁盘I/O次数 = 归并树的WPL * 2 16 = 读磁盘的次数 = 写磁盘的次数
要让磁盘I/O次数最少， 就要使归并树WPL最⼩ ——哈夫曼树
构造2路归并的最佳归并树如下
4.1.3 多路归并的情况
WPL = (9+30+12+18+3+17+2+6+24) * 2 = 242
归并过程中 磁盘I/O总次数=484次
多路归并的最佳归并树
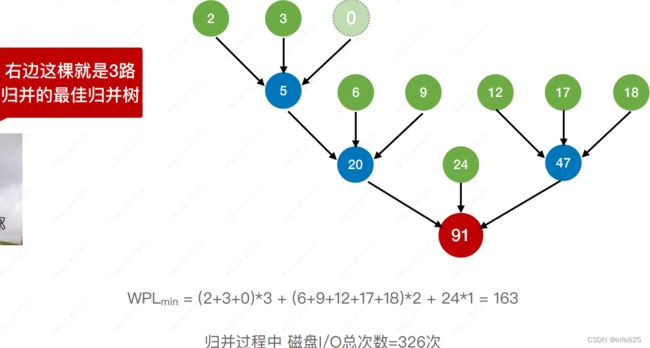
下面这棵就是3路 归并的最佳归并树
WPLmin = (2+3+6)*3 + (9+12+17+24+18)*2 + 30*1= 223
归并过程中 磁盘I/O总次数=446次
注意：对于k叉归并，若初始归并段的数量⽆法构成严格的 k 叉归并树， 则需要补充⼏个⻓度为 0 的“虚段”，再进⾏ k 叉哈夫曼树的构造。
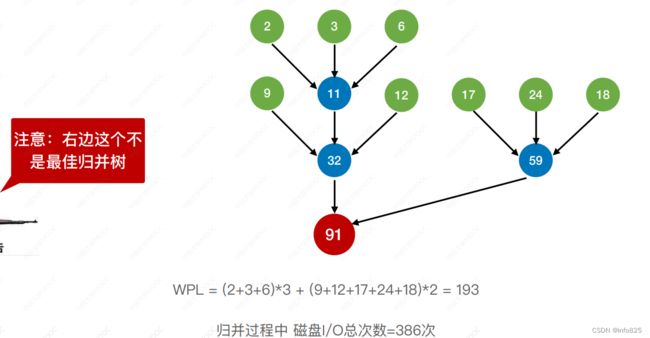
而直接构造是错误的
添加虚段的数量
k叉的最佳归并树⼀定是⼀棵严格的 k 叉树，即树中只包含度为k、度为0 的结点。 设度为k的结点有 
个，度为0的结点有 n0 个 ，归并树总结点数=n 则：
初始归并段数量+虚段数量=n0
（严格的 k 叉树所有节点的度出度+1根结点等于结点总数）
