机器学习-激活函数的直观理解

机器学习-激活函数的直观理解

在机器学习中，激活函数（Activation Function）是用于引入非线性特性的一种函数，它在神经网络的每个神经元上被应用。

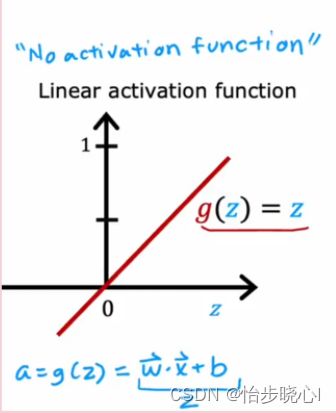
如果不使用任何的激活函数，那么神经元的响应就是wx+b，相当于线性的。由此，任意数量的线性激活的神经元叠加，其功能和单个线性激活的神经元一致（线性叠加后仍然是线性的）。

1、几种常用的激活函数

线性激活函数：也相当于没有激活函数，其作用相当于线性叠加：

---

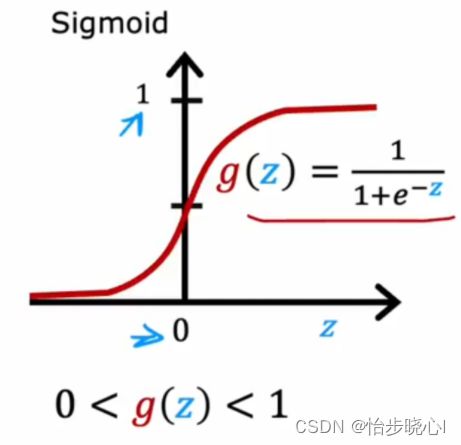
Sigmoid函数：Sigmoid函数是一个典型的逻辑函数，它会将任何实数映射到0到1之间。然而，它在输入值非常大或非常小的时候，会出现梯度消失的问题。f(x) = 1 / (1 + e^(-x))

---

Tanh函数：Tanh函数与Sigmoid函数非常相似，它会将任何实数映射到-1到1之间。和Sigmoid函数一样，它也存在梯度消失的问题。Tanh函数相对于原点对称，在处理某些具有对称性的问题时，Tanh可能会比Sigmoid更有优势。f(x) = (e^x - e^(-x)) / (e^x + e^(-x))

---

ReLU函数：ReLU（Rectified Linear Unit）是一种常用的激活函数，它对负数输出0，对正数则直接输出该数值。由于其简单性和在多层神经网络中的表现，ReLU在很多深度学习模型中得到了应用。但是它可能会在训练过程中出现神经元“死亡”的情况。f(x) = max(0, x)

死亡：当神经网络的权重更新导致神经元的输入变为负值，由于ReLU函数的特性，其输出将会为0，并且在后续的训练中，该神经元的输出将一直保持为0，因此某些神经元会不起作用。

---

Leaky ReLU：为了解决ReLU的“死亡”神经元问题，人们提出了Leaky ReLU激活函数。Leaky ReLU允许负数的小斜率，这样即使输入是负数，神经元也不会完全失效。在x小于0时有一个极小的负斜率。

---

Softmax函数：Softmax函数常用于多分类神经网络的输出层，因为它可以给出输入数据属于每个类别的概率。

---

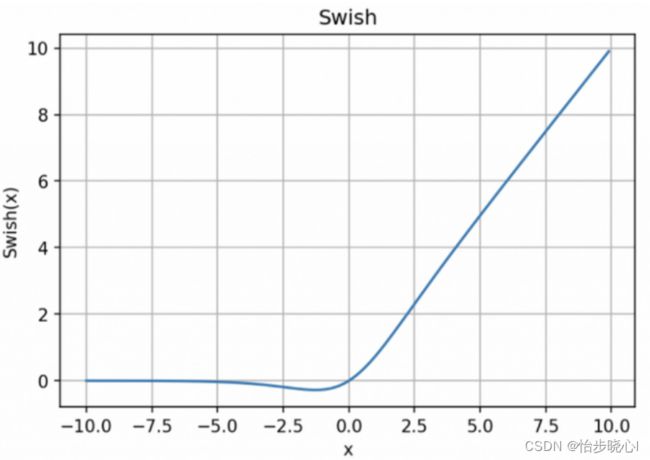
Swish函数：Swish是一种自门控激活函数，它在深度学习模型中表现出了优于ReLU的性能。Swish函数的形状介于ReLU和Sigmoid之间。f(x) = x * sigmoid(βx)

2、激活函数的直观理解

让我们来拟合一个函数，其目标如下所示：

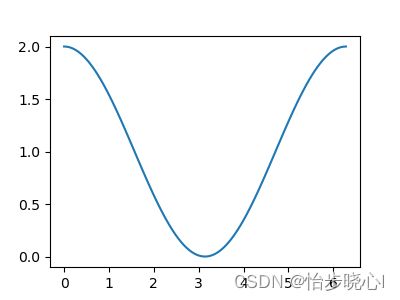
使用两层网络进行建模，其中第一层包含两个神经元（激活函数如下待定），第二层包含一个线性激活的神经元。

线性激活函数：首先使用线性激活函数作为第一层两个神经元的激活函数，训练得出的最终结果如下所示，由此可见多个线性激活神经元等效于一个神经元，因为最终得到的还是线性函数：

---

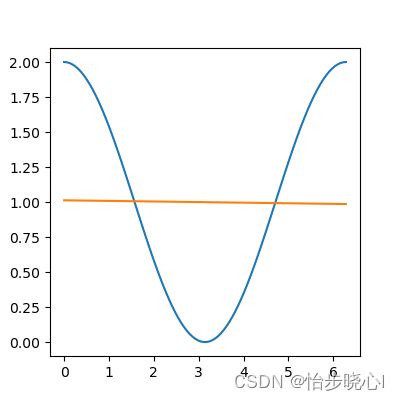
ReLU函数：其次使用ReLU函数作为第一层两个神经元的激活函数，在理想的情况下会得到如下的拟合结果，相当于是两个ReLU函数的组合，一个是直接向左平移，一个是翻转后平移：


但是ReLU在训练时可能会出现神经元死亡现象（上面解释过了），此时继续迭代也不会给性能带来提升（相当于陷入局部最优了），如：

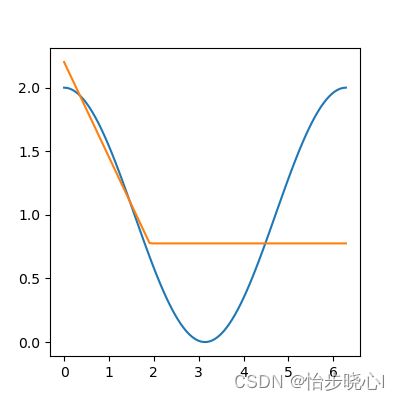
由此可见，激活函数就是拟合的最小单元。

---

Leaky ReLU：使用Leaky ReLU可以避免ReLU在训练时导致的死亡现象，每次训练都能得到满意的结果：

Sigmoid函数：Sigmoid函数在此处实际上更有优势，因为其实际上就是一个连续的曲线（Tanh同理）：

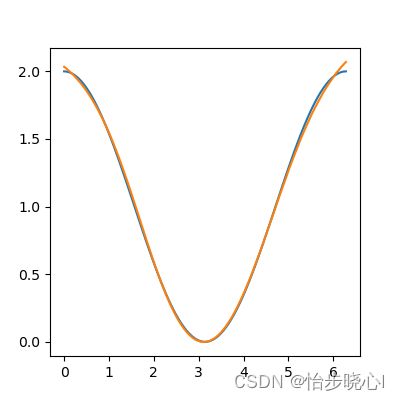
总结：激活函数就是拟合最终结果的最小单元，最终结果就是激活函数的平移反转或多次计算。上面的例子第二层是线性激活，因此最终结果相当于是第一层结果的线性叠加

3、结论分析

总结：激活函数就是拟合最终结果的最小单元，最终结果就是激活函数的平移反转或多次计算。上面的例子第二层是线性激活，因此最终结果相当于是第一层结果的线性叠加

显然，如果将第一层的两个神经元改为1个，就只会使用一个激活函数去进行拟合，Sigmoid的案例如;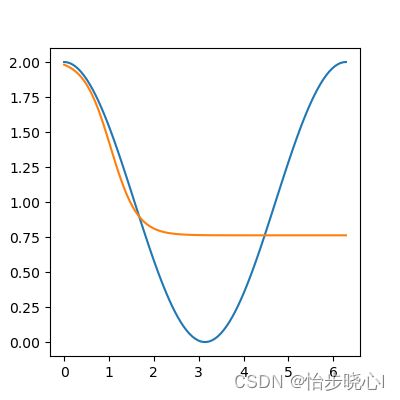

4、代码

# 引入相关的包
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from keras.models import Sequential
from keras.layers import Dense
import warnings
warnings.simplefilter(action='ignore', category=UserWarning)
# 创建要拟合的函数
X = np.linspace(0,2*np.pi, 100)
y = np.cos(X)+1
X=X.reshape(-1,1)
# 画图（可选）
fig,ax = plt.subplots(1,1, figsize=(4,3))
ax.plot(X,y)
plt.show()
# 构建模型
model = Sequential(
    [
        # Dense(2, activation="linear", name = 'l1'),
         Dense(2, activation="sigmoid", name = 'l1'),
        # Dense(2, activation="tanh", name='l1'),
        # Dense(2, activation="relu", name='l1'),
        # Dense(2, activation="leaky_relu", name='l1'),
        # Dense(2, activation="swish", name='l1'),
        Dense(1, activation="linear", name = 'l2')
    ]
)
model.compile(
    loss=tf.keras.losses.MeanSquaredError(),
    optimizer=tf.keras.optimizers.Adam(0.04),
)
model.fit(
    X,y,
    epochs=300
)
# 进行模型预测
yhat = model.predict(X)
fig,ax = plt.subplots(1,1, figsize=(4,4))
ax.plot(X,y)
ax.plot(X,yhat)
plt.show()
# 进行模型预测
l1 = model.get_layer('l1')
l2 = model.get_layer('l2')
l1.get_weights()
l2.get_weights()