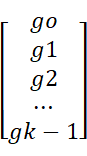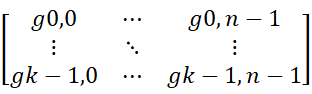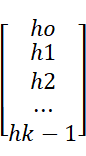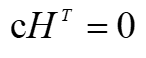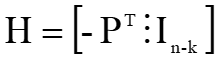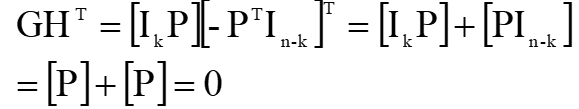P02114065刘浩宇，P02114070程韩奇，P02114066吴其，P02114068张璐——深入理解线性分组码的生成矩阵和校验矩阵定义及其关系

目录

前言

线性分组码

定义

性质

生成矩阵和校验矩阵

生成矩阵

生成矩阵的定义

生成矩阵的特性

校验矩阵

校验矩阵的定义

校验矩阵的特性

生成矩阵和校验矩阵的关系

---

前言

由于移动通信存在干扰和衰落，在信号传输过程中将出现差错，故对数字信号必须采用纠、检错技术，即纠、检错编码技术，以增强数据在信道中传输时抵御各种干扰的能力，提高系统的可靠性。对要在信道中传送的数字信号进行的纠、检错编码就是信道编码。通常纠错码分为两大类，即分组码和卷积码。该篇文章主要介绍线性分组码的生成矩阵和校验矩阵。

线性分组码

定义

当分组码的信息码元与监督码元之间的关系为线性关系时（用线性方程组联系），这种分组码就称为线性分组码。包括汉明码和循环码。

线性分组码可以概括为如下的一个线性映射：

前面的映射函数指的是线性性质的映射，后面的GF(2)指的是伽罗华域，通俗来讲就是所有的数据位要么取0，要么取1，就是数据是二进制的形式。

描述一个线性分组码一般有个简便的记法，叫(n, k)线性分组码，k是原始数据的长度，n是原始数据经过编码后的码字长度。

性质

线性分组码有以下重要性质：

全0的信息比特对应的码字也是全0的。

C（n，k）是一组码，其中每两个码相模二加减得到的码字依然在这组码中。

生成矩阵和校验矩阵

线性分组码生成矩阵(generate matrix, G)和校验矩阵(parity matrix, H)信道编码器将输入为的k - bit信息编码成)的n — bit 信息（n > k)。从线性代数向量空间的角度看，线性分组码(n, k)是n元组(n-tuples）向量空间V中的k维的子空间，存在k个线性独立的码字，形成基向量，张成(spanned)码字空间C。每一个码字v可以看成是以输入信息u作为系数的基向量的线性组合，如下式所示:

矩阵G称为线性分组码的校验矩阵(parity matrix)。线性分组码(n, k)是由矩阵G的行向量张成的子空间，也即G的行空间。由上面的秩-零度定理可知，矩阵G的零空间N(G)的维度为n —k。因而可以找出n —k个线性独立的向量，张成G的零空间N(G)，如下所示，ho, h1,... , hn_1张成了G的零空间N(G)。

可以得出:

因为有，

因此有:

矩阵H称为线性分组码的校验矩阵(parity matrix)。

生成矩阵G和检验矩阵Ⅱ的实现是多个经典线性分组码BCH码、RS码、LDPC码设计的核心。

生成矩阵

生成矩阵的定义

若 G 为一矩阵，它生成线性码 C 的码字的方式为，

w = s G,

其中 w 是线性码 C 的一个码字，而 s 是任意向量。 线性  码的生成矩阵的格式为 ，其中 n 为码字的长度，k 为信息比特的数量（作为向量子空间的 C 的维数），d 为码的最小距离，而 q 为有限域的大小, 即字典中符号的个数（因此 q = 2 表示二元码，等等。）冗余比特的数量用 r = n - k 表示。

生成矩阵的标准形式为：

 其中  是 k×k 单位矩阵而 P 是 k×r 矩阵。当生成矩阵为标准形式时，码 C 在其前 k 个坐标位置为系统码。

生成矩阵可以用来构建一个码的奇偶检验矩阵（反过来也可以）。如果生成矩阵 G 是标准形式 ，那么 C 奇偶校验矩阵就是,

 其中  是 P 矩阵的转置。这是由于 C 的奇偶检验矩阵是对偶码  的一个生成矩阵 

生成矩阵的特性

1.生成矩阵 一定是K 行N 列的K*N 阶矩阵，该生成矩阵的每行构成一行矢量，共有K个行矢量。

2.线性分组码的每个码字是生成矩阵各行矢量的线性组合。

显然，当为全零信息分组时，为全零序列 

3.的每一行是一个码字。因为若信息分组 ，则；若，则；依此类推，若 ，则。

4.生成矩阵的各行线性无关。

5.如果生成矩阵不具备式的形式，则由该生成矩阵产生的（nk） 线性分组码为非系统码。然而，对于任意的（）线性分组码，总可通过初等行变换及列交换将它的非系统码生成矩阵变换为另一等价的系统码的生成矩阵。此两等价生成矩阵生成的两个  线性分组码的检、纠错性能是相同的。

校验矩阵

校验矩阵的定义

与任何一个(n,k)分组线性码的码空间C相对应,一-定存在一个对偶空间D。事实上，码空间基底数k只是n维n重空间全部n个基底的一.部分,若能找出另外n-k个基底，也就找到了对偶空间D。既然用k个基底能产生一个(n,k)分组线性码，那么也就能用n-k个基底产生包含个码字的(n,n-k)分组线性码，称(n,n- k)码是(n,k)码的对偶码。

将D空间的n-k个基底排列起来可构成一个(n-k)Xn矩阵,将这个矩阵称作码空间C的校验矩阵,而它正是(n,n- k)对偶码的生成矩阵,它的每一行是对偶码的一个码字。 C和D的对偶是相互的,G是C的生成矩阵又是D的校验矩阵,而H是D的生成矩阵,又是C的校验矩阵。

校验矩阵的特性

（1）由H矩阵可以建立线性分组码的线性方程组,矩阵共有（n-k）行, 其中每行代表一个线性方程的系数, 表示求一个监督位的线性方程; 

（2）H矩阵的每行与码集中的一个码字的内积为 0 ;

（3）任何一个（n，k）线性分组码的矩阵有（n-k） 行, 且每行线性无关;

（4）系统码的系统生成矩阵  可以方便的得到系统校验矩阵  。

生成矩阵和校验矩阵的关系

由于C的基底和D的基底正交,空间C和空间D也正交,它们互为零空间,因此,(n,k)

线性码的任意码字c一定正交于其对偶码的任意-一个码字,也必定正交于校验矩阵H的任

意一个行矢量,即

式中,0代表零阵，它是1X(n- k)全零矢量。上式可以用来检验一个n重矢量是否为码字:若等式成立(得零矢量),该n重必为码字，否则必不是码字。

由于生成矩阵的每个行矢量都是一个码字，因此必有：

这里,0代表kX(n- k)的零矩阵。

系统生成矩阵为：

则校验矩阵：

上述负号在二进制情况下可以省略，因为模2减法和模2加法是等同的。

下面验证上式成立