c++学习之哈希
目录
1.关于unordered系列关联式容器
2.关于unordered_map
3.哈希(散列)表的实现
一,直接定址法
二,除留余数法
方法一:闭散列:开放定址法
方法二:闭散列:哈希桶/拉链法
4.哈希表的封装
哈希表封装后
unordered_map简单封装
unordered_set简单封装
1.关于unordered系列关联式容器
unordered_map和unordered_set是最常用的两个容器,它们的底层结构都是哈希,unordered_map是存储
在unordered_map中,键值通常用于惟一地标识元素,而映射值是一个对象,其内容与此键关联。键和映射值的类型可能不同。在内部,unordered_map没有对
unordered_set是一个存储唯一元素的集合,它的底层结构也是哈希表。它的元素是不可重复的,因此它的查询速度非常快。
2.关于unordered_map
先来看看库中的介绍:
对于map,还是以key_value为数据模型的,那么这里的key肯定也是不可以修改的,unodered_map强调的是查找效率,其次对于其迭代器是单向的。
对于它的接口也大差不差,,但是有两个我们没见过的,实际上在实现unordered_map中引入了其他参数及接口,如这里的负载因子(load_factor),哈希桶(Buckts).
3.哈希(散列)表的实现
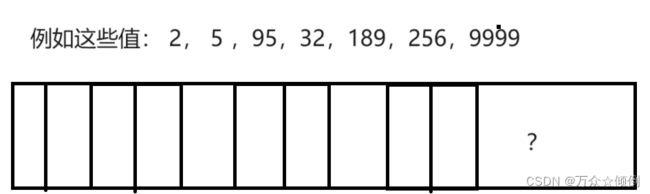
一,直接定址法
数据集中的时候我们开辟空间就小,但太分散时,如2作为key值插入位置2,95作为key插入位置95,9999插入位置9999.那对于空间无疑是巨大的浪费,那该怎么办呢?
二,除留余数法
有人就提出太大,那就对这个数取模,让它处在在一个合适的位置,比如上面7个数据,size为7,那就对每个数据模7,使它在这里个范围之内。
但是会出现新的问题,可能有数据会冲突,她两模完值是一样的,但对应的value是不一样的,这种问题被叫做哈希碰撞/哈希冲突,那么如何解决哈希碰撞呢?这时候有两种法案可以解决:
方法一:闭散列:开放定址法
本质上就是如果新插入的数据的位置已经有数据了(value不一样),那就在这个开放的空间中,重新找一个空位置。这里也会有两种查找新位置的方法--1.线性探测(一个个往后找)2.二次探测(以2次方递增查找)。
如果冲突,我们就往后找没有被占的位置。可是当我们的后面空间快要满员时,此时再往后找新的位置,就可能位置存在不够的情况,那么在实际上,插入数据的个数在空间达到70%等的时候就需要扩容了,这里我么就引入了一个参数-负载因子(存储关键字的个数/空间大小)来空间空间大小。
为什么会有两种探测或者其他方式来寻找都是避免多次冲突,比如对于线性探测,重新找位置的话,如果有一部分数据是连续的,一个位置被提前占了,那么就会引起一片的哈希冲突,面对这个问题因此有了的探测二次探测。
那么我们就先来实现一下哈希表:
对于这里的负载因子,即不能太大,也不能太小,太大,容易发生冲突,太小,空间浪费太多。
这里我们一般使用0.7较为合适。
namespace myspace
{
using namespace std;
//如何去插入首先就需要对插入的每个位置做标记,该位置下可能存在三种状态,已经有数据,为空,之前有现在删除了
enum State
{
EXIST,
EMPTY,
DELETE
};
//存放哈希表的数据的类型
templatestruct HashData
{
pair _kv;
State _sta=EMPTY;
};
//类型转换,计算出key的大小,来确定平衡因子
templatestruct HahFunc
{
size_t operator()(const K&k)
{
return size_t(k);
}
};
template<>struct HahFunc
{
//如果是字符串,我们用所有字符的ascll的和表示key
//但是字符串之和也是有很大可能重合,很多人通过在数学方面的研究出了一些解决办法
//这里最好的方式是采用的BKDR方法,给每个字符乘以31,131....这样的数 之后的和大概率不会重复
size_t operator()(const string& k)
{
size_t sum = 0;
for (int i = 0; i < k.size(); i++)
{
sum = sum * 31;
sum=sum+k[i];
}
return sum;
}
};
template>class HashTable
{
public:
HashTable()
{
//初始化空间为
tables.resize(10);
}
bool insert( const pair& kv)
{
if (find(kv.first) != NULL)
{
return false;
}
//负载因子决定是否扩容
if (_n * 10 / tables.size() == 7)
{
//扩容
//注意这里的扩容不能直接扩容,因为扩容之后size发生改变,对应的位置发生改变,因此需要重新开辟空间
//在一个个重新(映射)插入,之后释放旧空间
size_t newsize = tables.size() * 2;//扩二倍
HashTable newHaTa;
newHaTa.tables.resize(newsize);//新表
for (int i = 0; i < tables.size(); i++)
{
newHaTa.insert(tables[i]._kv);//重新走一遍映射再插入其中
}
//现在的需要的哈希表是新的,交换过来
tables.swap(newHaTa.tables);
}
//通过取模size使得对应的位置在该size内
Hash hf;
size_t hashi = hf(kv.first % tables.size()) ;
while (tables[hashi]._sta == EXIST)
{
//先确定好位置
hashi++;
hashi %= tables.size();
}
//再插入
tables[hashi]._kv = kv;
tables[hashi]._sta = EXIST;
_n++;
return true;
}
HashData* find(const K &key)
{
Hash hf;
size_t hashi = hf(key % tables.size());
while (tables[hashi]._sta!=EMPTY )
{
if (tables[hashi]._sta==EXIST&&
tables[hashi]._kv.first == key)
{
return &tables[hashi];
}
hashi++;
hashi %= tables.size();
}
return NULL;
}
//伪删除
bool erase(const K&key)
{
HashData tmp = find(key);
if (tmp)
{
tmp._sta == DELETE;
_n--;
return true;
}
else
{
return false;
}
}
void Printf()
{
for (int i = 0; i < tables.size(); i++)
{
if (tables[i]._sta == EXIST)
{
cout<< i<<" " << tables[i]._sta << "->" << tables[i]._kv.first << endl;
}
else if (tables[i]._sta == DELETE)
{
cout << i <<" " << "DELETE" << tables[i]._kv.first << endl;
}
else if (tables[i]._sta == EMPTY)
{
cout << i <<" " << "EMPTY" << tables[i]._kv.first << endl;
}
}
}
private:
vector> tables;
size_t _n;//插入的关键字的个数
};
}
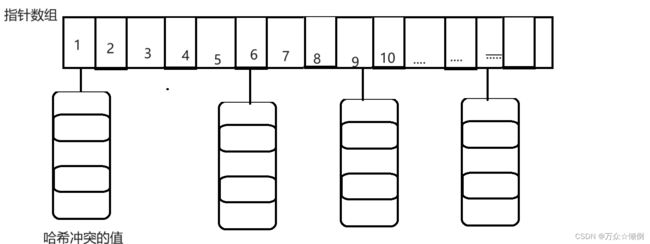
方法二:闭散列:哈希桶/拉链法
不同于上述的除留余数法,在实际的应用当中,而是引用哈希桶的方法,所谓的哈希桶,就是将哈希冲突的值放一起内部处理,此时整体结构就是vecor型的结构。
每一个key对应有一个桶,相同也没事,放在一起内部解决。
我来们可以将上面的挂着的链表理解为桶,里面存放着相同key的值,但是当存放的值太多,遍历桶里的值时间复杂度就是O(N),效率太低,因此当长度达到某个界限时,就会换成红黑树来存放,提高查找效率。
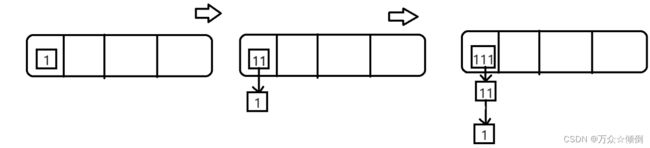
在结构上,vector中的list,我们为了实现迭代器,我们自己写单链表,里面存放Node*,再插入时,我们采用头插的方式,如下图假设1,11,111他们的key值一样。
由于key类型不一定是整形,也有可能是其他类型,对于字符换类型,我们选他们的ascll码之和,再称31,用仿函数转化为size_t,以此来表示位置。
namespace Hash_Bucket
{
using namespace std;
templatestruct HahFunc
{
size_t operator()(const K& k)
{
return size_t(k);
}
};
template<>struct HahFunc
{
//如果是字符串,我们用所有字符的ascll的和表示key
//但是字符串之和也是有很大可能重合,很多人通过在数学方面的研究出了一些解决办法
//这里最好的方式是采用的BKDR方法,给每个字符乘以31,131....这样的数 之后的和大概率不会重复
size_t operator()(const string& k)
{
size_t sum = 0;
for (int i = 0; i < k.size(); i++)
{
sum = sum * 31;
sum = sum + k[i];
}
return sum;
}
};
template struct HashNode
{
pair _kv;
HashNode* next;
HashNode(const pair& kv):_kv (kv),next(nullptr)
{
}
};
template>class HashTable
{
public:
typedef HashNode Node;
HashTable()
{
_table.resize(10);
}
~HashTable()
{
//循环遍历释放桶的每一个节点
for (int i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
while (cur)
{
Node* next = cur->next;
delete cur;
cur = next;
}
_table[i] = nullptr;
}
}
bool insert(const pair& kv)
{
Hash hf;
if (find(kv.first))
{
//不插入相同的值
return false;
}
//对于哈希桶,如果满了就要扩容,也就是负载因子为1
if (_n == _table.size())
{
//第一种扩容方式,我们延续上面的扩容方式
//size_t newsize = _table.size() * 2;//扩二倍
//HashTable newHaTa;
//newHaTa.tables.resize(newsize);//新表
//for (int i = 0; i < _table.size(); i++)
//{
// Node* cur = _table[i];
// while (cur)
// {
//newHaTa.insert(cur->kv);//重新走一遍映射再插入其中
// }
//
//}
现在的需要的哈希表是新的,交换过来
//_table.swap(newHaTa.tables);
//没必要用上述方式,我们直接重新弄个表,把节点挪动下来
vector newtable;
newtable.resize(2 * _table.size());
for (int i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
while (cur)
{
Node* Next = cur->next;
//重新映射到新表当中
size_t hashi = hf(kv.first) % newtable.size();
//头插
cur->next = newtable[i];
//表中的新头
newtable[i] = cur;
cur = Next;//遍历下一个
}
//旧表置空
_table[i] == nullptr;
}
//交换旧表与新表
_table.swap(newtable);
}
//还是先通过取模节省空间
size_t hashi = hf(kv.first) % _table.size();
//头插
Node* newnode = new Node(kv);
newnode->next = _table[hashi];
_table[hashi] = newnode;
++_n;
return true;
}
Node* find( const K&key)
{
Hash hf;
size_t hashi = hf( key) % _table.size();
Node* cur = _table[hashi];
while (cur)
{
if (cur->_kv.first == key)
{
return cur;
}
cur = cur->next;
}
return NULL;
}
bool erase(const K* key)
{
Hash hf;
size_t hashi = hf(key )% _table.size();
Node* cur = _table[hashi];
Node* prev = nullptr;
while (cur)
{
if (cur->_kv.first == key)
{
//找到并删除
//头删
if (prev == nullptr)
{
_table[hashi] = cur->next;//如果头被断开为空,cur的下一个就是新头节点
}
else
{
prev->next = cur->next;//和相对的头节点断开关系
}
delete cur;
return true;
}
prev = cur;//上一个节点,相对下一节点的头节点
cur = cur->next;//下一个节点
}
return false;
}
//那么实际上我们来看桶的大小其实并不会很大
void Some()
{
size_t bucketSize = 0;
size_t maxBucketLen = 0;
size_t sum = 0;
double averageBucketLen = 0;
for (size_t i = 0; i < _table.size(); i++)
{
Node* cur = _tables[i];
if (cur)
{
++bucketSize;
}
size_t bucketLen = 0;
while (cur)
{
++bucketLen;
cur = cur->_next;
}
sum += bucketLen;
if (bucketLen > maxBucketLen)
{
maxBucketLen = bucketLen;
}
}
averageBucketLen = (double)sum / (double)bucketSize;
printf("all bucketSize:%d\n", _tables.size());
printf("bucketSize:%d\n", bucketSize);
printf("maxBucketLen:%d\n", maxBucketLen);
printf("averageBucketLen:%lf\n\n", averageBucketLen);
}
void Print()
{
for (size_t i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
while (cur)
{
if (cur)
{
cout << cur->_kv.first << cur->_kv.second << endl;
}
cur = cur->next;
}
}
cout << endl;
}
private:
vector _table;//这里存放节点指针,目的是为了实现迭代器
size_t _n;
}; 可能有些人觉得哈希桶可能太长,效率可能太低 ,但实际上哈希桶并不会太长,通过BKDR,以及负载因子的控制,不会有太多相同的key值。因此哈希桶实现的哈希表效率与上述基本不差。4.
4.哈希表的封装
对于哈希表的封装,和封装红黑树一样,我们可以封装出unordered_map与unordered_map。
首先就是统一哈希表的模板参数,直接传pair,哈希表中用T表示,通过仿函数传T张key的类型,
之后就是实现迭代器,迭代器与哈希表两者相互依赖,需要提前声明,以及再哈希表中声明友元迭代器方便我们使用,在之后为了实现const迭代器,在传入参数Ref,Ptr作为T&,T*.
对于迭代器的封装,这里我们需要三个参数,分别是哈希表(也可用vector),结点指针,以及下标位置hashi,通过遍历判断实现前置++。
哈希表封装后
namespace Hash_Bucket
{
using namespace std;
templatestruct HahFunc
{
size_t operator()(const K& k)
{
return size_t(k);
}
};
template<>struct HahFunc
{
//如果是字符串,我们用所有字符的ascll的和表示key
//但是字符串之和也是有很大可能重合,很多人通过在数学方面的研究出了一些解决办法
//这里最好的方式是采用的BKDR方法,给每个字符乘以31,131....这样的数 之后的和大概率不会重复
size_t operator()(const string& k)
{
size_t sum = 0;
for (int i = 0; i < k.size(); i++)
{
sum = sum * 31;
sum = sum + k[i];
}
return sum;
}
};
template struct HashNode
{
T _data;
HashNode* next;
HashNode(const T& data):_data (data),next(nullptr)
{
}
};
//迭代器
//由于迭代器与哈希表存在双向依赖
//我们在这里给上前置声明
templateclass HashTable;
templatestruct HTiterator
{
typedef HashNode< T > Node;
HTiterator(Node*node, HashTable< K, T, keyofT, Hash>* _tab,size_t _hashi):_node(node), tab(_tab),hashi(_hashi)
{
}
//这里除了传一个指针,还需要数组或整个表
Node* _node;
const HashTable< K, T, keyofT, Hash>* tab;
size_t hashi;
typedef HTiterator< K, T, Ref,Ptr,keyofT, Hash > self;
//后置加加
self &operator++()
{
if (_node->next)
{
//继续走这个桶
_node = _node->next;
}
else
{
//下一个桶,找下一个桶
++hashi;
//新的桶
while (hashi < tab->_table.size())
{
if (tab->_table[hashi])
{
//如果不为空,我的节点就是这个新节点
_node = tab->_table[hashi];
break;
}
else {
++hashi;
}
}
if (hashi == tab->_table.size())
{
_node = nullptr;
}
}
return *this;
}
Ptr operator->()
{
return &(_node->data);
}
Ref operator*()
{
return (_node->_data);
}
bool operator!=(const self &tmp)
{
return _node != tmp._node;
}
};
template>class HashTable
{
public:
//声明友元
templatefriend struct HTiterator;
typedef HTiterator< K, T,T&,T*, keyofT, Hash > iterator;
typedef HTiterator< K, T, const T&, const T*, keyofT, Hash > const_iterator;
iterator begin()
{
for (int i = 0; i < _table.size(); i++)
{
if (_table[i])
{
return iterator(_table[i],this,i);
}
}
return end();
}
iterator end()
{
return iterator(nullptr, this,-1);
}
const_iterator begin()const
{
for (int i = 0; i < _table.size(); i++)
{
if (_table[i])
{
return const_iterator(_table[i], this, i);
}
}
return end();
}
const_iterator end()const
{
return const_iterator(nullptr, this, -1);
}
typedef HashNode Node;
HashTable()
{
_table.resize(10);
}
~HashTable()
{
//循环遍历释放桶的每一个节点
for (int i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
while (cur)
{
Node* next = cur->next;
delete cur;
cur = next;
}
_table[i] = nullptr;
}
}
Hash hf;
keyofT kot;
bool insert(const T& data)
{
if (find(kot(data)))
{
return false;
}
//对于哈希桶,如果满了就要扩容,也就是负载因子为1
if (_n == _table.size())
{
vector newtable;
newtable.resize(2 * _table.size());
for (int i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
while (cur)
{
Node* Next = cur->next;
//重新映射到新表当中
size_t hashi = hf(kot(data)) % newtable.size();
//头插
cur->next = newtable[i];
//表中的新头
newtable[i] = cur;
cur = Next;//遍历下一个
}
//旧表置空
_table[i] == nullptr;
}
//交换旧表与新表
_table.swap(newtable);
}
//还是先通过取模节省空间
size_t hashi = hf(kot(data)) % _table.size();
//头插
Node* newnode = new Node(data);
newnode->next = _table[hashi];
_table[hashi] = newnode;
++_n;
return true;
}
Node* find( const K&key)
{
Hash hf;
size_t hashi = hf( key) % _table.size();
Node* cur = _table[hashi];
while (cur)
{
if (kot(cur->_data) == key)
{
return cur;
}
cur = cur->next;
}
return NULL;
}
bool erase(const K* key)
{
Hash hf;
size_t hashi = hf(key )% _table.size();
Node* cur = _table[hashi];
Node* prev = nullptr;
while (cur)
{
if (kot(cur->data) == key)
{
//找到并删除
//头删
if (prev == nullptr)
{
_table[hashi] = cur->next;//如果头被断开为空,cur的下一个就是新头节点
}
else
{
prev->next = cur->next;//和相对的头节点断开关系
}
delete cur;
return true;
}
prev = cur;//上一个节点,相对下一节点的头节点
cur = cur->next;//下一个节点
}
return false;
}
//那么实际上我们来看桶的大小其实并不会很大
void Some()
{
size_t bucketSize = 0;
size_t maxBucketLen = 0;
size_t sum = 0;
double averageBucketLen = 0;
for (size_t i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
if (cur)
{
++bucketSize;
}
size_t bucketLen = 0;
while (cur)
{
++bucketLen;
cur = cur->_next;
}
sum += bucketLen;
if (bucketLen > maxBucketLen)
{
maxBucketLen = bucketLen;
}
}
averageBucketLen = (double)sum / (double)bucketSize;
printf("all bucketSize:%d\n", _table.size());
printf("bucketSize:%d\n", bucketSize);
printf("maxBucketLen:%d\n", maxBucketLen);
printf("averageBucketLen:%lf\n\n", averageBucketLen);
}
void Print()
{
for (size_t i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
while (cur)
{
if (cur)
{
cout << kot(cur->data) << kot(cur->data) << endl;
}
cur = cur->next;
}
}
cout << endl;
}
private:
vector _table;//这里存放节点指针,目的是为了实现迭代器
size_t _n;
};
}; unordered_map简单封装
namespace myspace1
{
using namespace std;
templateclass unordered_map
{
struct mapkeyofT
{
const K& operator()(const pair& data)
{
return data.first;
}
};
public:
typedef typename Hash_Bucket::HashTable< K, pair, mapkeyofT >::iterator iterator;
iterator begin()
{
return table.begin();
}
iterator end()
{
return table.end();
}
bool insert(const pair& kv)
{
return table.insert(kv);
}
private:
Hash_Bucket::HashTable, mapkeyofT> table;
};
void test()
{
unordered_map dictionary;
dictionary.insert(std::make_pair("苹果", "两个"));
dictionary.insert(std::make_pair("梨子", "两个"));
dictionary.insert(std::make_pair("香蕉", "两个"));
unordered_map::iterator it = dictionary.begin();
while (it != dictionary.end())
{
cout << (*it).first<< (*it).second<<" ";
++it;
}
}
}; unordered_set简单封装
namespace myspace2
{
templateclass unodered_set
{
struct setkeyofT
{
const K& operator()(const K& key)
{
return key;
}
};
public:
typedef typename Hash_Bucket::HashTable< K,K>, setkeyofT >::iterator iterator;
iterator begin()
{
return table.begin();
}
iterator end()
{
return table.end();
}
bool insert(const K& key)
{
return table.insert(key);
}
private:
Hash_Bucket::HashTable table;
};
};