密码学在实际应用中的加密技术

一直以来，有很多小伙伴在区块链学习亦或是网络安全学习的过程中，后台私聊我一些关于密码学的问题。在这篇文章里，我将尝试用通俗的语言，还原密码学应用逻辑与信息传输加密方法，帮助大家在密码学学习过程中更好的理解学科中的关键要点。希望无论是新手小白，还是在密码学学习道路上不断探索的“我们”，都能够通过这篇文章，收获一二。

密码，最初的目的是用于对信息加密，但随着密码学的运用，密码还被广泛用于身份认证、防止否认等问题上。针对信息传输过程中可能面对的“窃听”、“篡改”、“假冒”、“否认”等安全性隐患，计算机领域衍生出种类繁多的密码技术，针对不同的应用场景，可以总结出下表：

威胁	特征	相应技术
窃听	破坏数据机密性	对称加密、非对称加密、混合加密
假冒	第三方假冒一方发送信息	消息认证码、数字签名、数字证书
篡改	破坏数据完整性	单向散列、消息认证码、数字签名、数字证书
否认	事后否认自己行为	数字签名、数字证书

一、加密——防止“窃听”

密码最基本的功能是信息的加解密，这就涉及到了密码算法。每个密码算法都基于相应的数学理论。密码学发展至今，已经产生了大量优秀的密码算法，通常分为两类：对称密码算法（Sysmmetric Cryptography）和非对称密码算法（Public-Key Cryptography，Asymmetric Cryptography），这两者的区别是是否使用了相同的密钥。

（1）对称密码算法（Sysmmetric Cryptography）

所谓对称加密，是信息传递双方用同一个密钥来进行加密解密，实践中最为常用，效率高。

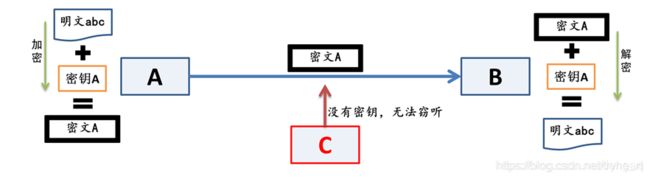
上图向大家展示了对称加密流程：

发送方A、接收方B共享密钥A；
发送方A通过密钥A对明文加密；
发送方A向接收方B发送密文；
接收方B通过密钥A解密密文，得到明文。
对称密码算法以A、B间密钥A的共享（传递）不被第三方C获取为前提，无法解决密钥分配过程中的安全性问题（即密钥A存在被第三方C获取的可能）。

（2）非对称密码算法（Public-Key Cryptography，Asymmetric Cryptography）

非对称加密可以用于解决密钥配送问题。

相对于对称密码加解密采用相同的密码，非对称密码加解密采用的是不同的密钥，公钥和私钥成对，公钥加密信息，相应的私钥解密。公钥是公开的，私钥归信息的接受者所有。由于非对称密码算法可以把加密密钥公开，因此也叫做公开密钥密码算法，简称公钥密码算法，或公钥算法。公钥算法非常优雅地解决了密钥既要保密又要公开的矛盾。

上图向大家展示了非对称加密流程：

接收方B生成公私钥对，私钥由接收方B自己保管；
接收方B将公钥发送给信息发送方A；
发送方A通过公钥对明文加密，得到密文；
发送方A向接收方B发送密文；
接收方B通过私钥解密密文，得到明文。
非对称加密算法似乎能够解决密钥分配问题，但是依然存在缺陷，其中最明显的缺陷是：加密解密效率慢！

RSA算法的速度是DES的1000分之一，并且密钥越长，速度会急剧变慢。基于此，在工业场景下，往往选择的是通过非对称加密配送密钥，对称加密加密明文的混合加密方式加密报文。

（3）混合加密

混合加密就是对称加密与非对称加密的结合。用对称密码来加密明文（速度），用非对称密码来加密对称密码中所使用的密钥（安全）。对称加密算法加密解密速度快，强度高，但存在密钥分配问题；非对称加密不存在密钥分配问题，但算法效率低。基于上述特征，可以选择通过非对称加密配送对称密钥，再采用对称密钥用来加密的方式，实现网络的密钥配送与通信加密，以取长补短，优化加密方法。

上图向大家展示了混合加密流程：

接收方B生成公私钥对（公钥A、私钥A），私钥（私钥A）由接收方B自己保管；
接收方B将公钥（公钥A）发送给信息发送方A；
发送方A通过公钥对对称密钥（对称密钥S）加密，得到密钥密文；
发送方A向接收方B发送密钥密文；
接收方B通过私钥（私钥A）解密密文，得到对称密钥（对称密钥S）；
此时，发送方A、接收方B成功共享密钥S，此后信息就可以用对称加密方法传递；
发送方A通过密钥S对明文加密；
发送方A向接收方B发送密文；
接收方B通过密钥S解密密文，得到明文。
混合加密利用对称加密算法解决了信息加解密效率缺陷，利用非对称加密算法配送对称密钥解决了密钥分配问题，但即便如此，仍然存在一定的安全隐患，如：无法避免中间人攻击、信息篡改

例如：中间人C可以在劫持B发出的公钥A后，发送一个伪造的公钥B给A，A通过公钥B加密后的密文，可以被劫持者C通过私钥B解密，之后所有的密文都对劫持者透明了；C还能用之前劫持到的公钥A 假冒 A，通过加密信息甚至篡改信息，发送给B，此时AB均无从发觉公钥已被中间人C 伪造，信息已被窃听，甚至篡改。

二、单向散列、消息认证码——防止“假冒”与“篡改”

加密算法为我们解决了数据的窃听威胁，但无法有效应对数据的篡改与假冒，这就有必要了解消息认证码等相关技术。

（1）单向散列技术（One-Way Hash Function）

在了解消息认证码前，我们需要先了解单向散列技术（即哈希技术）。所谓单向散列技术又称密码检验（Cryptographic Checksum）、指纹 （Fingerprint）、消息摘要 （Message Digest），是为了保证信息的完整性（Integrity），防止信息被篡改的一项技术。单向散列算法，又称单向Hash函数、杂凑函数，就是把任意长的输入消息串变化成固定长的输出串且由输出串难以得到输入串的一种函数。其具有如下特点：

1、任意的消息大小。哈希函数对任何大小的消息x都适用。
2、固定的输出长度。无论信息长度，计算出的长度永远不变。
3、计算快速，即函数的计算相对简单
4、具有单向性(one-way)，不可由散列值推出原信息。即教材所谓的抗第一原像性【给定一个输出z，找到满足h(x)=z的输入x是不可能的】
5、信息不同，散列值不同，具有抗碰撞性(Collision Resistance)。

（1）强抗碰撞性：要找到散列值相同的两条不同的消息是非常困难的（知道散列值找两条消息）。即找到满足h(x1)=h(x2)的一对x1≠x2在计算上是不可行的；
（2）弱抗碰撞性：要找到和该消息具有相同散列值的另一个消息是非常困难的（知道该消息和其散列值找另一条消息）。即抗第二原像性【给定x1和h(x1)，找到满足h(x1)=h(x2)的x2在计算上是不可能的】。

常见的单向散列函数(Hash函数)有消息摘要算法MD（Message Digest）、安全散列算法SHA（Secure Hash Algorithm），其中采用 Keccak 算法的SHA-3采用海绵结构。就安全性而言，MD4、MD5为产生128比特散列值，均已不安全，存在可碰撞。SHA-1产生160比特散列值，也是不推荐使用的，存在可碰撞。RIPEMD-128、RIPEMD-160也不推荐使用。推荐使用SHA-2、SHA-3算法（目前对它的支持还不是很广泛）。

哈希函数是没有密钥的。哈希函数两个最主要的应用就是数字签名和消息验证码(比如 HMAC)
哈希函数的三个安全性要求为单向性、抗第二原像性和抗冲突性。
为了抵抗冲突攻击，哈希函数的输出长度至少为160 位；对长期安全性而言，最好使用256位或更多的哈希函数。
MD5 的使用非常广泛，但却是不安全的。人们发现了 SHA-1中存在的严重安全漏洞，这样的哈希函数应该被逐步淘汰。SHA-2算法看上去是安全的。
正在进行的 SHA-3竞争将在几年后产生新的标准化的哈希函数。
结合密码学的加解密技术和单向散列技术，有了用于防止篡改的消息认证码技术，防止伪装的数字签名技术以及认证证书，这一部分请看下文。

（2）消息认证码（Message Authentication Code）

消息认证码算法（MAC）的作用在于验证传输数据的完整性，这就要求其应当是一串需要与共享密钥相关而且足够有区分度的串。因此，可以通过多种方式获得 MAC 值，如单向散列（Hash函数）、分组密码截取最后一组作为 MAC 值、流密码、非对称加密等。

以单向散列技术（Hash函数）为例：

首先，消息认证码采用的是对称加密，因此A需要准备一个用于加密密文的密钥（密钥W）和一个用来生成消息验证码的密钥（密钥X），将其通过安全的方法（如非对称加密算法）发送给接收方B。

上图向大家展示了密钥建立共享后信息的传输流程：

发送方 A 与接收方 B 共享密钥（加密密文的密钥W和生成消息验证码的密钥X）；
发送方A通过密钥W对明文加密，得到密文；
发送方 A 通过密钥X计算 MAC 值，hash加密后生成消息验证码（MAC-A）；
发送方A向接收方B发送密文和消息验证码（MAC-A）；
接收方 B 对密文通过密钥X计算 MAC 值，再hash加密一次获得消息验证码（MAC-B）。
接收方 B 比较 MAC-A 与 MAC-B，若一致则说明信息未被篡改，可以通过密钥W对密文解密读取信息。
若MAC-A 与 MAC-B不一致，则说明密文被篡改，或者消息验证码被篡改，或两者皆被篡改。
需要注意的是，消息认证码仍然存在问题：

密钥配送的问题，因为 MAC 需要发送者与接收者使用相同的密钥；
暴力破解；
无法防止事后否认、也无法对第三方证明。因为密钥是共享的，接收者可以伪造对发送者不利的信息。
重放攻击，窃取某一次通信中的正确的 MAC，然后攻击者重复多次发送相同的信息。由于信息与 MAC 可以匹配，在不知道密钥的情况下，攻击者就可以完成攻击。
以下方法可以避免重放攻击：

序号，约定信息中带上递增序号，MAC 值为加上序号的 MAC
时间戳，约定信息中带上时间戳。使用时间戳避免重放攻击要保证发送者和接受者的时钟必须一致，但考虑到网络延迟，必须在时间的判断上留下缓冲，因此仍有可以进行重放攻击的时间。
随机数 nonce，每次传递前，先发送随机数 nonce，通信时再将随机数包含在消息中并计算MAC值，基于此将无法进行重放。

三、数字签名、数字证书——防止“事后否认”，兼顾“假冒”与“篡改”

（1）数字签名

消息验证码之所以无法解决事后否认的问题，是因为其采用的是对称加密算法（因为密钥是共享的，接收者存在伪造发送者信息之可能，因此发送者可以事后否认信息的真实性。），采用非对称加密的消息认证码的技术，就是数字签名。

在非对称加密中，私钥用来解密，公钥用来加密。
在数字签名技术中，私钥用来加密，公钥用来解密。

上图向大家展示了数字签名及验证流程：

签名方 A 生成非对称公私钥对 公钥A、私钥A；
A 向消息接收方 B 发送公钥A；
A 使用私钥A对消息加密（一般是对消息的散列值进行加密，防止因数据量过大或非对称加密效率低下特征导致签名时间过长等问题），生成数字签名；
A 将消息与数字签名发往 B；
接收方B通过公钥解密数字签名；
验证签名，即比对Hash值，如相等，大概率（存在Hash碰撞）表明数据未被篡改。
用更为归纳性的语言表述，即先计算消息的散列值，再对散列值进行私钥加密，得到的即为签名，签名人将消息和签名发送，接收方用公钥对签名进行解密并做验证（只要接收方B能够用A的公钥解密数字签名，就代表该签名是A签署的，因为公钥A只能解锁由A保管的私钥A签写的签名）。

当然数字签名的方式也有两种：

明文签名：不对消息进行加密，只对消息进行签名，主要用于发布消息。
密文签名：对消息进行加密和签名。
数字签名不仅能够防止A的事后否认，同样能够防止数据的假冒与篡改。但需要注意的是，数字签名仍然存在问题：

数字签名由于采用了非对称加密算法，尽管能够防止否认，但发送方却不能知道所收到的公钥是否是接收方私钥所对应的公钥，因此无法防止中间人攻击。

伪造公钥是中间人攻击中重要的一环。之所以能够伪造，是因为消息发送方无法确认公钥的身份问题。如下图所示，如果公钥A被中间人C所劫持，替换成自己的公钥C，接受者B采用了攻击者C的公钥，此后接收了攻击者私钥签名的信息，公私钥完全匹配，AB均无从发觉公钥已被中间人C 伪造、篡改。

（2）数字证书

对数字签名所发布的公钥进行权威的认证，便是证书。公钥证书记录个人信息及个人公钥，并由认证机构施加数字签名。数字证书能够有效避免中间人攻击的问题。

为实现不同成员在不见面的情况下进行安全通信，公钥基础设施（PKI）当前采用的模型是基于可信的第三方机构，也就是证书颁发机构（CA）签发的证书。PKI是为了能够有效的运用公钥而制定的一系列规范和规格的总称（并非某单一规范）。其组成包括用户、认证机构（CA）、证书仓库。其中证书颁发机构（CA）是指我们都信任的证书颁发机构，它会在确认申请用户的身份之后签发证书。同时CA会在线提供其所签发证书的最新吊销信息（CRL，证书作废清单），用户要定期查询认证机构最新的CRL，确认证书是否失效。

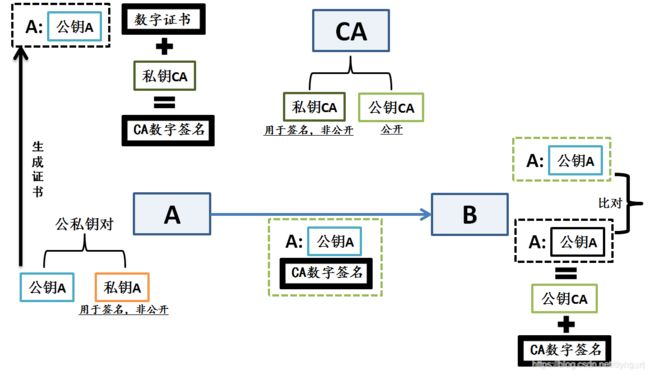
上图向大家展示了数字证书的生成及验证流程：

A 生成公私钥对；
A 向认证中心CA注册自己的公钥A（该步骤只在第一次注册时存在）；
认证中心CA用自己的私钥（私钥CA）对A的公钥（公钥A）施加数字签名并生成数字证书；
B得到带有认证机构CA的数字签名的A的公钥（证书）；
B使用认证机构CA的公开公钥（公钥CA）验证数字签名，确认公钥A的合法性。
对于认证机构的公钥，一般由其它的认证机构施加数字签名，从而对认证机构的公钥进行验证，即生成一张认证机构的公钥证书，这样的关系可以迭代好几层，以杜绝中间人假冒认证机构CA。最高一层的认证机构被称为根CA，RCA会对自己的公钥进行数字签名，即自签名，也会在RCA间互相签名。

这与https加密传输原理是一致的。以CSDN站点为例，我们先从CSDN的证书中拿到CSDN的公钥，对我们本地生成的对称加密密钥进行加密，此后发送给CSDN,CSDN用其私钥解密获得我们的对称加密密钥，此时本地计算机与CSDN就拥有相同的对称密钥，此后用对称加密和消息认证码、数字签名来防止信息传输中的窃听、假冒、篡改以及事后否认。

密码学是一门非常有趣的学科，它与计算机科学、数学以及电子工程都存在交叉。随着密码学日新月异地取得发展，人们现在已经很难跟上它的发展步伐。密码学领域的理论基础在过去的30余年里已经得到加强和巩固：现在，人们对安全的定义和证明结构安全的方法有了更深入的认识。同时，我们也见证了应用密码学的快速发展：旧算法不断地被破解和抛弃，同时，新算法和协议也在不断涌现。

之所以写这篇文章，是为了能够以最通俗易懂的方式帮助大家快速了解现代加密方案的工作原理。但由于抛开了微积分等必要的数学概念以及个人知识理解的局限性，所以，难免在相关问题的表述上略显稚嫩，供期望更深入理解现代密码学的读者以参考借鉴，也欢迎大家的批评交流。

————————————————
版权声明：本文为CSDN博主「邓大帅」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/deng_xj/article/details/106786151