校园导游程序及通信线路设计(结尾附着总源码)
校园导游程序及通信线路设计
摘 要
新生或来访客人刚到校园,对校园的环境不熟悉。就需要一个导游介绍景点,推荐到下一个景点的最佳路径等。随着科技的发展,社会的进步,人们对便捷的追求也越来越高。为了减少人力和时间。针对对校外人员来访对环境的不熟悉,本次课设运用C++语言和Visual Studio工具开发了一种便捷系统。该系统能够让外来人员迅速了解学校的布局,并且减少的迷路等问题的发生,并且可以走最短的路逛遍整个校园。
关键字:导游系统;C++; 最短路径; 通信线路铺设
目 录
1 功能需求…………………………………………………1
1.1 功能任务……………………………………………………1
1.2 使用的开发工具……………………………………………1
1.3 设计的界面…………………………………………………1
1.4 预期指标说明………………………………………………1
2 概要设计…………………………………………………2
2.1 数据结构……………………………………………………2
2.2 操作…………………………………………………………2
3 详细设计…………………………………………………4
3.1 数据结构类型定义…………………………………………4
3.2 操作的算法…………………………………………………5
4 程序实现…………………………………………………7
5 程序测试…………………………………………………15
5.1 正常情况……………………………………………………15
5.2 异常情况……………………………………………………19
6 个人心得建议……………………………………………20
1 功能需求
1.1 功能任务:
设计校园平面图,所含景点不少于10个。以图中顶点表示校内各景点,存放景点名称、代号、简介等信息;以边表示路径,存放路径长度等相关信息。
(1) 显示校园平面图 (2) 景点信息查询
(3) 任意2个景点的路径查询 (4) 通信线路设计
1.2 开发工具:Visual Studio
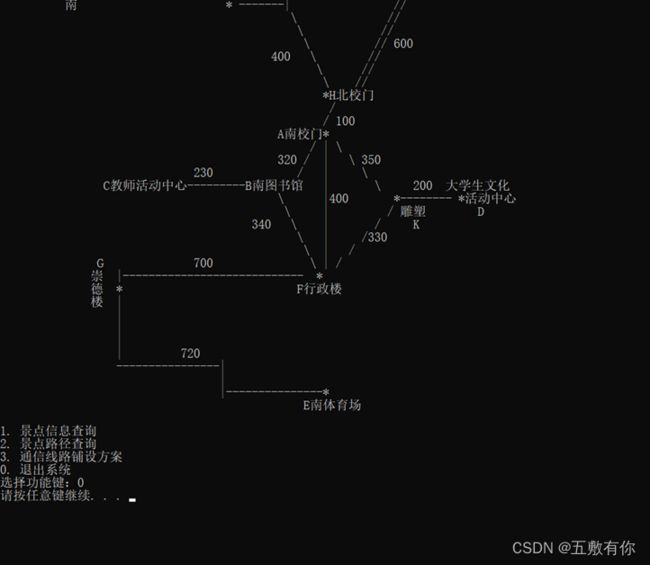
1.3 设计界面:
1.4 预取指标说明:
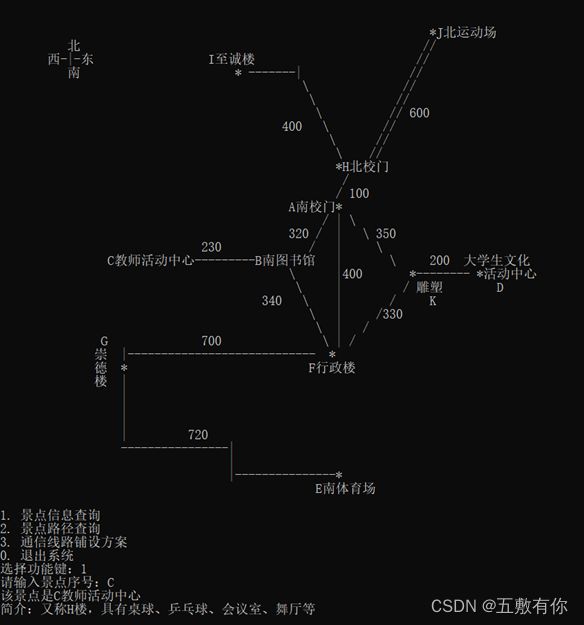
(1) 显示校园平面图
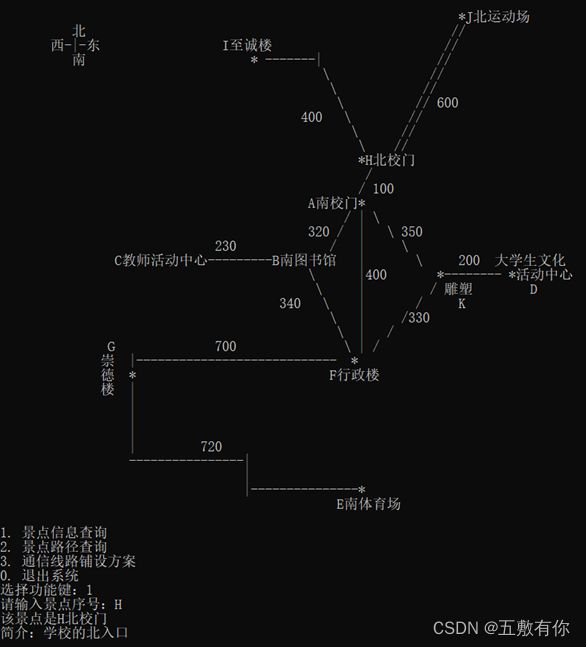
(2) 景点信息查询:为来访客人提供图中任意景点相关信息的查询。
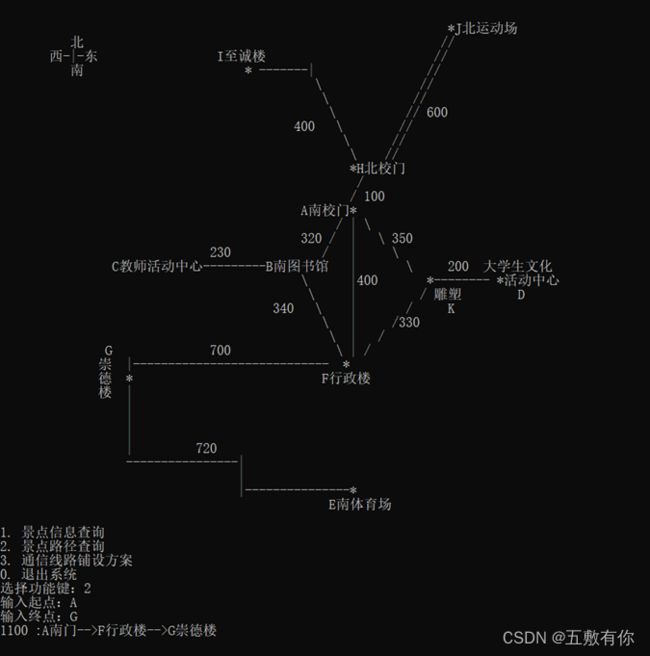
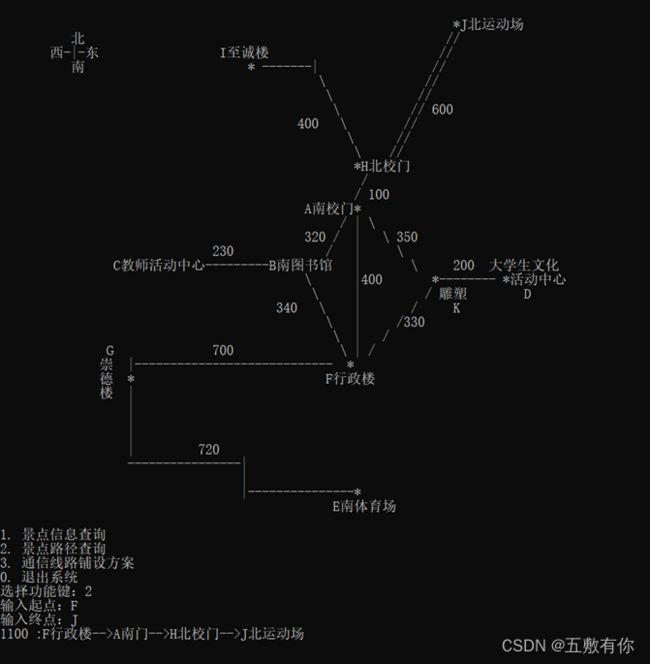
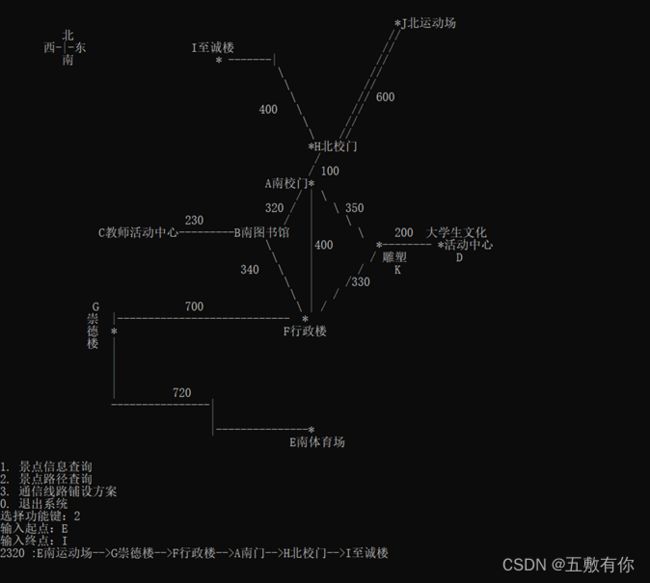
(3) 任意2个景点的路径查询:为来访客人提供图中任意2个景点的问路查询,即查询任意两个景点之间的一条最短的简单路径及距离。
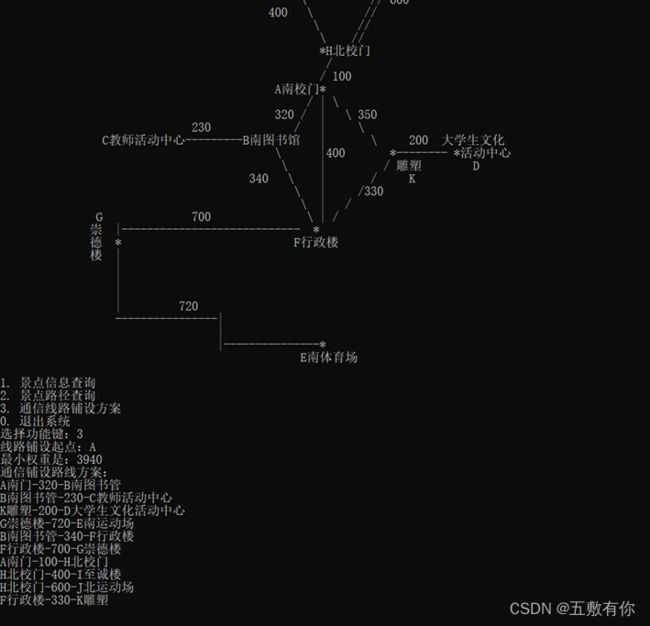
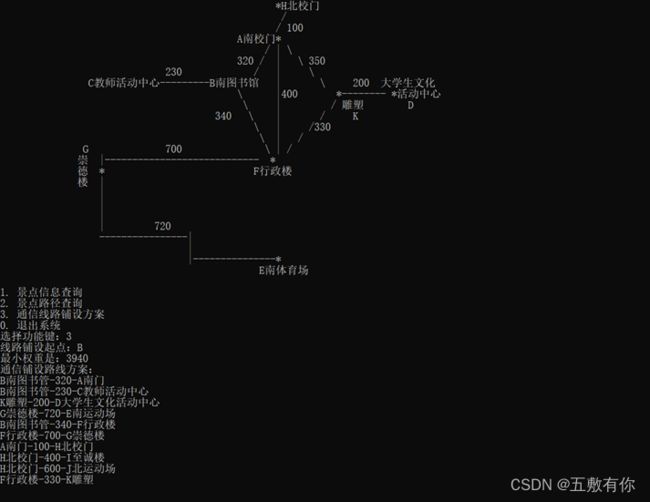
(4) 通信线路设计:以尽可能低的造价建造景点间的通信网络把这些景点联系在一起,每条通信线路的造价与景点间的距离成正比。给出铺设方案
2 概要设计
2.1 数据结构
选取图的顺序存储结构和链式存储结合的存储方式结构,采用邻接表存储方式。
2.2 操作
int Locate(ALGraph* G, char c) //获取顶点的下标
void Creat_ALGraph(ALGraph* G) //创建邻接表
void information(ALGraph* G) //获取各个顶点的信息
int getEweight(ALGraph* G, int i, int j) //得到i-j边的权重
void shortestPath(ALGraph* G, int p[], float D[])//起点到终点最短路径
void prim(ALGraph* G, int tree[], int cost[]) //最小生成树
void view_show() //显示地图
main() //程序启动入口
main()Creaat_ALGraph *G,char)创建地图,调用view_show() 来显示地图,调用information(ALGraph* G)获取各个顶点的信息 调用shortestPath(ALGraph* G, int p[], float D[]) 获取起点到终点的最短距离。调用prim (ALGraph* G, int tree[], int cost[])获取铺设线路的最小花费,即最小生成树。
Information(ALGraph* G)调用 Locate(ALGraph* G, char c)来获取顶点下标
void shortestPath(ALGraph* G, int p[], float D[])调用Locate(ALGraph* G, char c)来获取顶点下标,再用getEweight(ALGraph* G, int i, int j)获得两点间边的权重。
Void prim (ALGraph* G, int tree[], int cost[])调用Locate(ALGraph* G, char c)来获取顶点下标,再用getEweight(ALGraph* G, int i, int j)获得两点间边的权重。
3 详细设计
3.1 数据结构类型定义
#define MAX 100 //开辟空间
#define MAXVALUE 10086 //假设为无穷大
int visit[MAX] = {0}; //是否访问
边结点的类型定义:
typedef struct edge
{
char adjvex; //邻接点域
int weight; //顶点到邻接点的边权重
struct edge* next; //指向下一个邻接点的指针域
}EdgeNode; //边结点
顶点结点的类型定义
typedef struct
{
char ch; //顶点结点的代表字符
string vertex; //顶点
string info; //顶点信息
EdgeNode* firstedge; //第一条边的指针
}VertexNode; //顶点结点
邻接表数据类型定义
typedef struct
{
VertexNode adjList[MAX]; //邻接表
int v_num; //顶点数
int e_num; //边数
}ALGraph;
3.2 操作的算法描述
int Locate(ALGraph* G, char c)
算法:获取到顶点字符,然后匹配所有的顶点,若找到返回下标,找不到返回-1。
void Creat_ALGraph(ALGraph* G)
算法:
第一步:初始化顶点。先先确定顶点数和边数,将各顶点名称录入,在依次录入顶点代表字符(方便游客使用),再录入顶点的信息。然后是把第一条边的指着置空。
第二步:初始化边。用两个字符数组来分别存储边的起点和终点 用整型数组来存储边的权值,再依次申请结点依次插入。
void information(ALGraph* G)
算法:输入景点字符后,开始匹配所以景点,如果找到则输出信息,没找到输出未找到该景点。
int getEweight(ALGraph* G, int i, int j)
算法:由形参获取边的起点和终点。然后获取起点结点的邻接点,分别与终点的代表符匹配,如果有这条边,则输出这个的边的权重。若没有则返回无穷大。
void shortestPath(ALGraph* G, int p[], float D[])
算法:1、向量D表示从源点Vm出发,到达图上各点Vi的可能最短路径长度,初值为:D[i]=getEweight(G,m,i );(m为源点下标) Vi ∈Vn.
2、选择Vj使得D[j]=min{D[i]|Vi∈Vn-S}
则Vj就是当前求得的从源点Vm出发的一条最短路径的终点,将Vj加入到S中:S=S∪{Vj}
3、修改从源点Vm出发到集合Vn-S上任意顶点Vk可能的最短路径长度。如果:(D[j] + getEweight(G, j, k) < D[k]),则修改D[k]为:D[k]=D[j]+ getEweight(G, j, k)。
重复操作2和3共n-1次。由此求得从源点Vm到图上其余个点的最短路径,即起点到终点Vn的路径。
void prim(ALGraph* G, int tree[], int cost[])
算法:输入源点,假设源点为u0即初始状态时U={u0};相应的表示:flag[0]=1;
它表示顶点u0加入到集合U中,然后从一端顶点属于U,另一端不属于U的所有边中选取权值最小的边,加入到tree中然后flag[k]=1,由于uk进入U,依次检查所有的(uk,uj)边的权值,是否小于原来的保存的最小边的权值,若是,则更新cost[j]为新的更小的边的权值,同时更新tree[j]=k,重复操作n-1次,最后tree中即为所建立起来的最小生成树。也就是铺设线路的最少花费。
4 程序实现
//获取顶点下标
int Locate(ALGraph* G, char c)
{ int count = 0;
for (int i = 0; i < G->v_num; i++)
{ if (c == G->adjList[i].ch)
{ return count; //若找到则返回
}
count++;
}
return -1;
}
//获取景点信息
void information(ALGraph* G)
{
int flag = 0;
char infor;
cout << "请输入景点序号:";
cin >> infor;
for (int i = 0; i < G->v_num; i++)
{
if (infor == G->adjList[i].ch) {
cout << "该景点是" << G->adjList[i].vertex << endl;
cout << "简介:";
cout << G->adjList[i].info;
flag = 1;
}
}
if (flag == 0)
{
cout << "没有该景点";
}
}
//得到路径上两点间的权重
int getEweight(ALGraph* G, int i, int j)
{
EdgeNode* p;
p = G->adjList[i].firstedge;
while (p)
{
if (G->adjList[j].ch == p->adjvex)
{
return p->weight;
}
p = p->next;
}
return MAXVALUE;
}
//两点间最短路径
void shortestPath(ALGraph* G, int p[], float D[])
{
int min;
int j=0;
char c;
int pre;
char c_d;
cout << "输入起点:";
cin >> c;
while (c < 'A' || c>'K')
{
cout << "起点输入错误,请重新输入:" << endl;
cin >> c;
}
cout << "输入终点:";
cin >> c_d;
while (c_d< 'A' || c_d>'K')
{
cout << "终点输入错误,请重新输入" << endl;
cin >> c_d;
}
int u = Locate(G, c);
for (int i = 0; i < G->v_num; i++)
{
D[i] = getEweight(G, u, i);
p[i] = u;
}
D[u] = 0; visit[u] = 1; p[u] = -1;
for (int i = 0; i < G->v_num; i++)
{
min = MAXVALUE + 1;
for (int k = 0; k < G->v_num; k++)
{
if (visit[k] == 0 && D[k] < min)
{
min = D[k];
j = k;
}
}
visit[j] = 1;
for (int k = 0; k < G->v_num; k++)
{
if (visit[k] == 0 && (D[j] + getEweight(G, j, k) < D[k]))
{
D[k] = D[j] + getEweight(G, j, k);
p[k] = j;
}
}
}
string temp[13];
int r = -1;
int f = Locate(G, c_d);
cout << D[f] << " :";
pre = p[f];
while (pre >= 0)
{
r++;
temp[r] = G->adjList[pre].vertex;
pre = p[pre];
}
while (r>=0)
{
cout << temp[r];
cout << "-->";
r--;
}
cout << G->adjList[f].vertex;
for (int i = 0; i < G->v_num; i++) //恢复
{
visit[i] = 0;
}
}
//通信线路铺设(最小生成树)
void prim(ALGraph* G, int tree[], int cost[])
{
int weight = 0;
visit[100] = { 0 };
int last=0;
int i, j, k=-8, mincost;
char cc;
cout << "线路铺设起点:";
cin >> cc;
while (cc > 'K' || cc < 'A')
{
cout << "起点输入错误,请重新输入:"<> cc;
}
int u = Locate(G, cc);
for (i = 0; i < G->v_num; i++)
{
if (u == i)
{
continue;
}
cost[i] = getEweight(G, u, i);//等于自己没有权重
tree[i] = u;
}
visit[u] = 1; tree[u] = -1; cost[u] = 0;
for (i = 1; i < G->v_num; i++)
{
mincost = MAXVALUE;
for (j = 0; j < G->v_num; j++)
{
if (visit[j] == 0 && cost[j] <= mincost)
{
mincost = cost[j];
k = j;
}
}
visit[k] = 1;
for (j = 0; j < G->v_num; j++)
{
if (visit[j] == 0 && getEweight(G, k, j) < cost[j])
{
cost[j] = getEweight(G, k, j);
tree[j] = k;
last = j;
}
}
}
for (int i = 0; i < G->v_num; i++)
{
weight += cost[i];
visit[i] = 0;
}
cout << "最小权重是:" << weight<v_num; i++)
{
if (i == u)
continue;
p = tree[i];
cout << G->adjList[p].vertex<<"-"<adjList[i].vertex< 5 程序测试
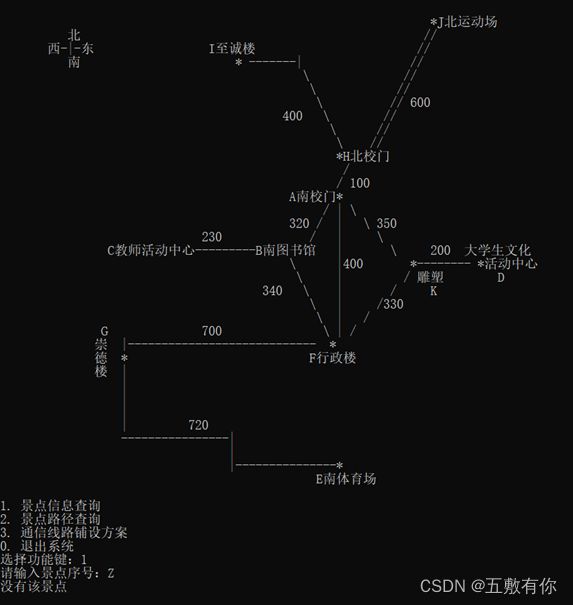
5.1 正常情况:
5.2 异常情况
6 总结个人心得体会及建议
通过这个课设我充分理解了图论的许多内容,邻接表方式存储,对入度出度的理解,最小生成树的prim算法,这个算法是刚开始输出的时候总是报错,后来我仔细阅读了相关资料发现tree[]存的是边,这个边不一定是连续的,但是他包括了所有顶点。最短路径的Dijkstra算法我也是有了更深理解,这里面的P[]存的是连续的边。
只有实践才能将理论变成现实。在设计过程中既训练了理论的理解和增强了动手能力。也在这个过程中发现问题、思考问题、解决问题。我对自己的建议是代码还是以实践为主,学习不能只停留在最初阶段,实践才是检验真理的唯一标准。
总源码:
#include
#include
using namespace std;
#define MAX 102 //开辟空间
#define MAXVALUE 10086 //无穷大
int visit[MAX] = { 0 };//未访问
typedef struct edge
{
char adjvex;
int weight;
struct edge* next;
}EdgeNode;
typedef struct
{
char ch;
string vertex;
string info;
EdgeNode* firstedge;
}VertexNode;
typedef struct
{
VertexNode adjList[MAX];
int v_num;
int e_num;
}ALGraph;
//定位下标
int Locate(ALGraph* G, char c)
{
int count = 0;
for (int i = 0; i < G->v_num; i++)
{
if (c == G->adjList[i].ch)
{
return count;
}
count++;
}
return -1;
}
//建表
void Creat_ALGraph(ALGraph* G)
{
int m, n;
EdgeNode* p, * q;
G->v_num = 11;
G->e_num = 12;
G->adjList[0].vertex = "A南门";
G->adjList[1].vertex = "B南图书管";
G->adjList[2].vertex = "C教师活动中心";
G->adjList[3].vertex = "D大学生文化活动中心";
G->adjList[4].vertex = "E南运动场";
G->adjList[5].vertex = "F行政楼";
G->adjList[6].vertex = "G崇德楼";
G->adjList[7].vertex = "H北校门";
G->adjList[8].vertex = "I至诚楼";
G->adjList[9].vertex = "J北运动场";
G->adjList[10].vertex = "K雕塑";
for (int i = 0; i < G->v_num; i++)
{
G->adjList[i].ch = char(int('A') + i);
}
G->adjList[0].info = "学校南入口";
G->adjList[1].info = "学校南侧的图书馆";
G->adjList[2].info = "又称H楼,具有桌球、乒乓球、会议室、舞厅等";
G->adjList[3].info = "团委、学生会、社联所在处";
G->adjList[4].info = "具有足球场、篮球场、羽毛球场等";
G->adjList[5].info = "计算机学院楼及其他行政办公";
G->adjList[6].info = "经管学院楼";
G->adjList[7].info = "学校的北入口";
G->adjList[8].info = "办理学生事务处";
G->adjList[9].info = "具有足球场、篮球场、健身房等";
G->adjList[10].info = "校园雕塑";
for (int i = 0; i < G->v_num; i++)
{
G->adjList[i].firstedge = NULL;
}
for (int i = 0; i < G->e_num; i++)
{
char ch_1[12] = { 'A','A','A','A','B','B','G','G','F','K','I','H' };
char ch_2[12] = { 'B','K','H','F','C','F','E','F','K','D','H','J' };
int weight_s[12] = { 320,350,100,400,230,340,720,700,330,200,400,600 };
p = new EdgeNode();
p->adjvex = ch_2[i];
p->weight = weight_s[i];
m = Locate(G, ch_1[i]);//狐尾
n = Locate(G, ch_2[i]);//虎头
p->next = G->adjList[m].firstedge;
G->adjList[m].firstedge = p;
q = new EdgeNode();
q->adjvex = ch_1[i];
q->weight = weight_s[i];
m = Locate(G, ch_1[i]);//虎头
n = Locate(G, ch_2[i]);//狐尾
q->next = G->adjList[n].firstedge;
G->adjList[n].firstedge = q;
}
}
//查询各景点信息
void information(ALGraph* G)
{
int flag = 0;
char infor;
cout << "请输入景点序号:";
cin >> infor;
for (int i = 0; i < G->v_num; i++)
{
if (infor == G->adjList[i].ch) {
cout << "该景点是" << G->adjList[i].vertex << endl;
cout << "简介:";
cout << G->adjList[i].info;
flag = 1;
}
}
if (flag == 0)
{
cout << "没有该景点";
}
}
//得到路径上两点间的权重
int getEweight(ALGraph* G, int i, int j)
{
EdgeNode* p;
p = G->adjList[i].firstedge;
while (p)
{
if (G->adjList[j].ch == p->adjvex)
{
return p->weight;
}
p = p->next;
}
return MAXVALUE;
}
//最短路径
void shortestPath(ALGraph* G, int p[], float D[])
{
int min;
int j = 0;
char c;
int pre;
char c_d;
cout << "输入起点:";
cin >> c;
while (c < 'A' || c>'K')
{
cout << "起点输入错误,请重新输入:" << endl;
cin >> c;
}
cout << "输入终点:";
cin >> c_d;
while (c_d < 'A' || c_d>'K')
{
cout << "终点输入错误,请重新输入" << endl;
cin >> c_d;
}
int u = Locate(G, c);
for (int i = 0; i < G->v_num; i++)
{
D[i] = getEweight(G, u, i);
p[i] = u;
}
D[u] = 0; visit[u] = 1; p[u] = -1;
for (int i = 0; i < G->v_num; i++)
{
min = MAXVALUE + 1;
for (int k = 0; k < G->v_num; k++)
{
if (visit[k] == 0 && D[k] < min)
{
min = D[k];
j = k;
}
}
visit[j] = 1;
for (int k = 0; k < G->v_num; k++)
{
if (visit[k] == 0 && (D[j] + getEweight(G, j, k) < D[k]))
{
D[k] = D[j] + getEweight(G, j, k);
p[k] = j;
}
}
}
string temp[13];
int r = -1;
int f = Locate(G, c_d);
cout << D[f] << " :";
pre = p[f];
while (pre >= 0)
{
r++;
temp[r] = G->adjList[pre].vertex;
pre = p[pre];
}
while (r >= 0)
{
cout << temp[r];
cout << "-->";
r--;
}
cout << G->adjList[f].vertex;
for (int i = 0; i < G->v_num; i++) //恢复
{
visit[i] = 0;
}
}
//通信线路铺设
void prim(ALGraph* G, int tree[], int cost[])
{
int weight = 0;
visit[100] = { 0 };
int last = 0;
int i, j, k = -8, mincost;
char cc;
cout << "线路铺设起点:";
cin >> cc;
while (cc > 'K' || cc < 'A')
{
cout << "起点输入错误,请重新输入:" << endl;
cin >> cc;
}
int u = Locate(G, cc);
for (i = 0; i < G->v_num; i++)
{
if (u == i)
{
continue;
}
cost[i] = getEweight(G, u, i);//等于自己没有权重
tree[i] = u;
}
visit[u] = 1; tree[u] = -1; cost[u] = 0;
for (i = 1; i < G->v_num; i++)
{
mincost = MAXVALUE;
for (j = 0; j < G->v_num; j++)
{
if (visit[j] == 0 && cost[j] <= mincost)
{
mincost = cost[j];
k = j;
}
}
visit[k] = 1;
for (j = 0; j < G->v_num; j++)
{
if (visit[j] == 0 && getEweight(G, k, j) < cost[j])
{
cost[j] = getEweight(G, k, j);
tree[j] = k;
last = j;
}
}
}
for (int i = 0; i < G->v_num; i++)
{
weight += cost[i];
visit[i] = 0;
}
cout << "最小权重是:" << weight << endl;
cout << "通信铺设路线方案:" << endl;
int p;
for (int i = 0; i < G->v_num; i++)
{
if (i == u)
continue;
p = tree[i];
cout << G->adjList[p].vertex << "-" << cost[i] << "-" << G->adjList[i].vertex << endl;
}
}
int getEweight(ALGraph* G, int i, int j);
void view_show();
int main()
{
int flag = 1;
int m, n;
int tree[100];//存储最小生成树
int cost[100];//存放边值
int P[MAX]; //相应最短路径点的前驱点
float D[MAX]; //存放起点到对应终点的的最短路径长度
ALGraph* G = new ALGraph();
cout << "河北大学地图如图所示:" << endl << endl;
Creat_ALGraph(G);
while (flag)
{
cout << endl << endl;
view_show();
cout << "1. 景点信息查询" << endl;
cout << "2. 景点路径查询" << endl;
cout << "3. 通信线路铺设方案" << endl;
cout << "0. 退出系统" << endl;
cout << "选择功能键:";
cin >> n;
switch (n)
{
case 1: {
information(G);
break;
}
case 2: {
shortestPath(G, P, D);
break;
}
case 3: {
prim(G, tree, cost);
break;
}
case 0: {
flag = 0;
break;
}
default:
cout << "功能键错误";
break;
}
}
system("pause");
return 0;
}
void view_show()
{
cout << endl;
cout << "\ *J北运动场 " << endl;
cout << "\ 北 // " << endl;
cout << "\ 西-|-东 I至诚楼 // " << endl;
cout << "\ 南 * -------| // " << endl;
cout << " \\ // " << endl;
cout << " \\ // " << endl;
cout << " \\ // 600 " << endl;
cout << " 400 \\ // " << endl;
cout << " \\ // " << endl;
cout << " \\ // " << endl;
cout << " \ *H北校门 " << endl;
cout << " \ / " << endl;
cout << " \ / 100 " << endl;
cout << " \ A南校门* " << endl;
cout << " \ / | \\ " << endl;
cout << " \ 320 / | \\ 350 " << endl;
cout << " \ 230 / | \\ " << endl;
cout << " \ C教师活动中心---------B南图书馆 | \\ 200 大学生文化 " << endl;
cout << " \\ |400 *-------- *活动中心 " << endl;
cout << " \\ | / 雕塑 D " << endl;
cout << " 340 \\ | / K " << endl;
cout << " \\ | /330 " << endl;
cout << " \\ | / " << endl;
cout << " G 700 \\ | / " << endl;
cout << "\ 崇 |---------------------------- * " << endl;
cout << "\ 德 * F行政楼 " << endl;
cout << "\ 楼 | " << endl;
cout << "\ | " << endl;
cout << "\ | " << endl;
cout << "\ | " << endl;
cout << "\ | 720 " << endl;
cout << "\ ----------------| " << endl;
cout << "\ | " << endl;
cout << "\ |---------------* " << endl;
cout << "\ E南体育场 " << endl;
cout << "\ " << endl;
}