数据结构与算法(Java)-树形DP题单
树形DP(灵神笔记)
543 二叉树的直径
543. 二叉树的直径 - 力扣(LeetCode)
给你一棵二叉树的根节点,返回该树的 直径 。
二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示。
示例 1:
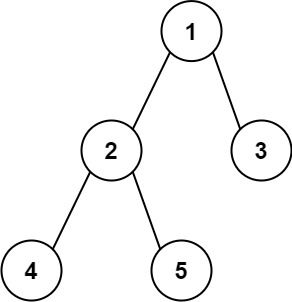
输入:root = [1,2,3,4,5]
输出:3
解释:3 ,取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。
示例 2:
输入:root = [1,2]
输出:1
提示:
- 树中节点数目在范围
[1, 104]内 -100 <= Node.val <= 100
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private int ans;
public int diameterOfBinaryTree(TreeNode root) {
dfs(root);
return ans;
}
private int dfs(TreeNode root) {
if (root == null) {
return -1;//返回-1 下面+1变成了0
}
int l_len = dfs(root.left) + 1;//左子树最大链长+1
int r_len = dfs(root.right) + 1;//右子树最大链长+1
ans = Math.max(ans, l_len + r_len);
return Math.max(l_len, r_len);
}
}
124 二叉树的最大路径和
124. 二叉树中的最大路径和 - 力扣(LeetCode)
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
示例 1:
输入:root = [1,2,3]
输出:6
解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
示例 2:
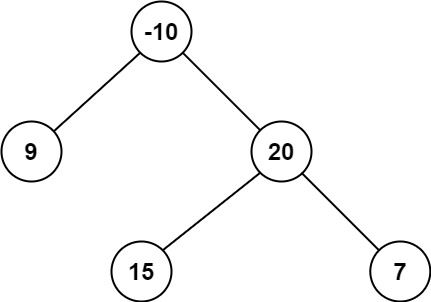
输入:root = [-10,9,20,null,null,15,7]
输出:42
解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
提示:
- 树中节点数目范围是
[1, 3 * 104] -1000 <= Node.val <= 1000
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private int ans = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
dfs(root);
return ans;
}
private int dfs(TreeNode root) {
if (root == null) {
return 0;//没有结点 和为0
}
int l_val = dfs(root.left);
int r_val = dfs(root.right);
ans = Math.max(ans, l_val + r_val + root.val);
return Math.max(Math.max(l_val, r_val) + root.val, 0);//负数不选
}
}
2246 相邻字符不同的最长路径
2246. 相邻字符不同的最长路径 - 力扣(LeetCode)
给你一棵 树(即一个连通、无向、无环图),根节点是节点 0 ,这棵树由编号从 0 到 n - 1 的 n 个节点组成。用下标从 0 开始、长度为 n 的数组 parent 来表示这棵树,其中 parent[i] 是节点 i 的父节点,由于节点 0 是根节点,所以 parent[0] == -1 。
另给你一个字符串 s ,长度也是 n ,其中 s[i] 表示分配给节点 i 的字符。
请你找出路径上任意一对相邻节点都没有分配到相同字符的 最长路径 ,并返回该路径的长度。
示例 1:
输入:parent = [-1,0,0,1,1,2], s = "abacbe"
输出:3
解释:任意一对相邻节点字符都不同的最长路径是:0 -> 1 -> 3 。该路径的长度是 3 ,所以返回 3 。
可以证明不存在满足上述条件且比 3 更长的路径。
示例 2:
输入:parent = [-1,0,0,0], s = "aabc"
输出:3
解释:任意一对相邻节点字符都不同的最长路径是:2 -> 0 -> 3 。该路径的长度为 3 ,所以返回 3 。
提示:
n == parent.length == s.length1 <= n <= 105- 对所有
i >= 1,0 <= parent[i] <= n - 1均成立 parent[0] == -1parent表示一棵有效的树s仅由小写英文字母组成
class Solution {
private List<Integer>[] g;//存储父节点i的子节点
private String s;
private int ans;
public int longestPath(int[] parent, String s) {
this.s = s;
int n = parent.length;
g = new ArrayList[n];
Arrays.setAll(g, e -> new ArrayList<>());
for (int i = 1; i < n; i++) {
//记录父节点的子节点的索引
g[parent[i]].add(i);
}
dfs(0);
return ans + 1;//求点的个数,路径长度+1
}
//计算最大长度
private int dfs(int x) {
int maxLen = 0;
for (int y : g[x]) {
int len = dfs(y) + 1;
if (s.charAt(x) != s.charAt(y)) {
ans = Math.max(ans, maxLen + len);//最长路径
maxLen = Math.max(maxLen, len);//左右子树最大长度
}
}
return maxLen;
}
}
687 最长同值路径
687. 最长同值路径 - 力扣(LeetCode)
给定一个二叉树的 root ,返回 最长的路径的长度 ,这个路径中的 每个节点具有相同值 。 这条路径可以经过也可以不经过根节点。
两个节点之间的路径长度 由它们之间的边数表示。
示例 1:
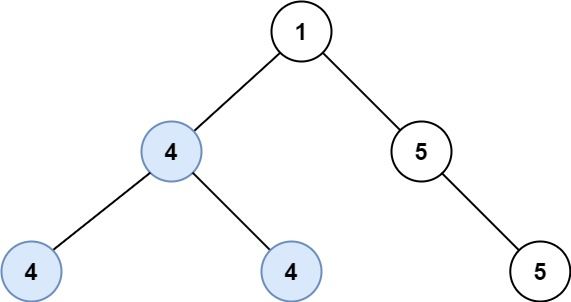
输入:root = [5,4,5,1,1,5]
输出:2
示例 2:
输入:root = [1,4,5,4,4,5]
输出:2
提示:
- 树的节点数的范围是
[0, 104] -1000 <= Node.val <= 1000- 树的深度将不超过
1000
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private int ans;
public int longestUnivaluePath(TreeNode root) {
dfs(root);
return ans;
}
private int dfs(TreeNode root) {
if (root == null) {
return -1;
}
int l_len = dfs(root.left) + 1;
int r_len = dfs(root.right) + 1;
if (root.left != null && root.left.val != root.val) {
l_len = 0;
}
if (root.right != null && root.right.val != root.val) {
r_len = 0;
}
ans = Math.max(ans, l_len + r_len);
return Math.max(l_len, r_len);
}
}
1617 统计子树中城市之间最大距离
参考题解:1617. 统计子树中城市之间最大距离 - 力扣(LeetCode)
给你 n 个城市,编号为从 1 到 n 。同时给你一个大小为 n-1 的数组 edges ,其中 edges[i] = [ui, vi] 表示城市 ui 和 vi 之间有一条双向边。题目保证任意城市之间只有唯一的一条路径。换句话说,所有城市形成了一棵 树 。
一棵 子树 是城市的一个子集,且子集中任意城市之间可以通过子集中的其他城市和边到达。两个子树被认为不一样的条件是至少有一个城市在其中一棵子树中存在,但在另一棵子树中不存在。
对于 d 从 1 到 n-1 ,请你找到城市间 最大距离 恰好为 d 的所有子树数目。
请你返回一个大小为 n-1 的数组,其中第 d 个元素(下标从 1 开始)是城市间 最大距离 恰好等于 d 的子树数目。
请注意,两个城市间距离定义为它们之间需要经过的边的数目。
示例 1:
输入:n = 4, edges = [[1,2],[2,3],[2,4]]
输出:[3,4,0]
解释:
子树 {1,2}, {2,3} 和 {2,4} 最大距离都是 1 。
子树 {1,2,3}, {1,2,4}, {2,3,4} 和 {1,2,3,4} 最大距离都为 2 。
不存在城市间最大距离为 3 的子树。
示例 2:
输入:n = 2, edges = [[1,2]]
输出:[1]
示例 3:
输入:n = 3, edges = [[1,2],[2,3]]
输出:[2,1]
提示:
2 <= n <= 15edges.length == n-1edges[i].length == 21 <= ui, vi <= n- 题目保证
(ui, vi)所表示的边互不相同。
class Solution {
private List<Integer>[] g;
private boolean[] inSet, vis;//inSet是选出来的树(城市) vis记录的是这个城市(树)的直径
private int[] ans;
private int n, diameter;//定义n和直径
public int[] countSubgraphsForEachDiameter(int n, int[][] edges) {
this.n = n;
g = new ArrayList[n];
Arrays.setAll(g, e -> new ArrayList<>());
for (var e : edges) {
int x = e[0] - 1;
int y = e[1] - 1;
g[x].add(y);
g[y].add(x);//建树
}
ans = new int[n - 1];
inSet = new boolean[n];
f(0);
return ans;
}
private void f(int i) {
if (i == n) {
for (int v = 0; v < n; v++) {
if (inSet[v]) {
vis = new boolean[n];
diameter = 0;
dfs(v);
break;
}
}
if (diameter > 0 && Arrays.equals(vis, inSet)) {
ans[diameter - 1]++;
}
return;
}
//不选城市i
f(i + 1);
//选城市i
inSet[i] = true;
f(i + 1);
inSet[i] = false;
}
//树的直径
private int dfs(int x) {
vis[x] = true;
int maxLen = 0;
for (int y : g[x]) {
if (!vis[y] && inSet[y]) {
int len = dfs(y) + 1;
diameter = Math.max(diameter, maxLen + len);
maxLen = Math.max(maxLen, len);
}
}
return maxLen;
}
}
2538 最大价值和与最小价值和的差值
参考题解:2538. 最大价值和与最小价值和的差值 - 力扣(LeetCode)
给你一个 n 个节点的无向无根图,节点编号为 0 到 n - 1 。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间有一条边。
每个节点都有一个价值。给你一个整数数组 price ,其中 price[i] 是第 i 个节点的价值。
一条路径的 价值和 是这条路径上所有节点的价值之和。
你可以选择树中任意一个节点作为根节点 root 。选择 root 为根的 开销 是以 root 为起点的所有路径中,价值和 最大的一条路径与最小的一条路径的差值。
请你返回所有节点作为根节点的选择中,最大 的 开销 为多少。
示例 1:
输入:n = 6, edges = [[0,1],[1,2],[1,3],[3,4],[3,5]], price = [9,8,7,6,10,5]
输出:24
解释:上图展示了以节点 2 为根的树。左图(红色的节点)是最大价值和路径,右图(蓝色的节点)是最小价值和路径。
- 第一条路径节点为 [2,1,3,4]:价值为 [7,8,6,10] ,价值和为 31 。
- 第二条路径节点为 [2] ,价值为 [7] 。
最大路径和与最小路径和的差值为 24 。24 是所有方案中的最大开销。
示例 2:
输入:n = 3, edges = [[0,1],[1,2]], price = [1,1,1]
输出:2
解释:上图展示了以节点 0 为根的树。左图(红色的节点)是最大价值和路径,右图(蓝色的节点)是最小价值和路径。
- 第一条路径包含节点 [0,1,2]:价值为 [1,1,1] ,价值和为 3 。
- 第二条路径节点为 [0] ,价值为 [1] 。
最大路径和与最小路径和的差值为 2 。2 是所有方案中的最大开销。
提示:
1 <= n <= 105edges.length == n - 10 <= ai, bi <= n - 1edges表示一棵符合题面要求的树。price.length == n1 <= price[i] <= 105
class Solution {
private List<Integer>[] g;
private int[] price;
private long ans;
public long maxOutput(int n, int[][] edges, int[] price) {
this.price = price;
g = new ArrayList[n];
Arrays.setAll(g, e -> new ArrayList<>());
for (var e : edges) {
int x = e[0], y = e[1];
g[x].add(y);
g[y].add(x);
}
dfs(0, -1);
return ans;
}
private long[] dfs(int x, int father) {
// maxS1前面最大带叶子的路径和 maxS2前面最大不带叶子的路径和
long p = price[x], maxS1 = p, maxS2 = 0;
for (var y : g[x]) {
if (y != father) {
var res = dfs(y, x);
// s1当前不带叶子的路径和 s2当前带叶子的路径和
long s1 = res[0], s2 = res[1];
ans = Math.max(ans, Math.max(maxS1 + s2, maxS2 + s1));
maxS1 = Math.max(maxS1, s1 + p);
maxS2 = Math.max(maxS2, s2 + p);// x必然不是叶子
}
}
return new long[]{maxS1, maxS2};
}
}
337 打家劫舍三
337. 打家劫舍 III - 力扣(LeetCode)
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。
示例 1:
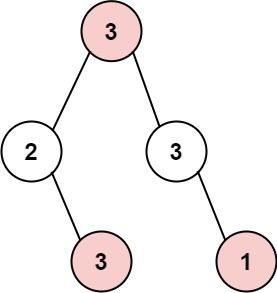
输入: root = [3,2,3,null,3,null,1]
输出: 7
解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7
示例 2:
输入: root = [3,4,5,1,3,null,1]
输出: 9
解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9
提示:
- 树的节点数在
[1, 104]范围内 0 <= Node.val <= 104
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int rob(TreeNode root) {
int[] ans = dfs(root);
return Math.max(ans[0], ans[1]);
}
private int[] dfs(TreeNode root) {
if (root == null) {
return new int[]{0,0};
}
int[] left = dfs(root.left);
int[] right = dfs(root.right);
int rob = left[1] + right[1] + root.val;//选根节点
//不选根节点
int notRob = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
return new int[]{rob, notRob};
}
}
1377 T秒后青蛙的位置
1377. T 秒后青蛙的位置 - 力扣(LeetCode)
参考题解:1377. T 秒后青蛙的位置 - 力扣(LeetCode)
建图(树)模版(以1377为例)
public static void main(String[] args) {
int n = 7;
int[][] edges = new int[][]{{1,2},{1,3},{1,7},{2,4},{2,6},{3,5}};
List<Integer>[] g = new ArrayList[n + 1];
Arrays.setAll(g, e -> new ArrayList<>());
for (var e : edges) {
int x = e[0], y = e[1];
g[x].add(y);
g[y].add(x); // 建树
}
}
给你一棵由 n 个顶点组成的无向树,顶点编号从 1 到 n。青蛙从 顶点 1 开始起跳。规则如下:
- 在一秒内,青蛙从它所在的当前顶点跳到另一个 未访问 过的顶点(如果它们直接相连)。
- 青蛙无法跳回已经访问过的顶点。
- 如果青蛙可以跳到多个不同顶点,那么它跳到其中任意一个顶点上的机率都相同。
- 如果青蛙不能跳到任何未访问过的顶点上,那么它每次跳跃都会停留在原地。
无向树的边用数组 edges 描述,其中 edges[i] = [ai, bi] 意味着存在一条直接连通 ai 和 bi 两个顶点的边。
返回青蛙在 t 秒后位于目标顶点 target 上的概率。与实际答案相差不超过 10-5 的结果将被视为正确答案。
示例 1:
输入:n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4
输出:0.16666666666666666
解释:上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳,第 1 秒 有 1/3 的概率跳到顶点 2 ,然后第 2 秒 有 1/2 的概率跳到顶点 4,因此青蛙在 2 秒后位于顶点 4 的概率是 1/3 * 1/2 = 1/6 = 0.16666666666666666 。
示例 2:
输入:n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7
输出:0.3333333333333333
解释:上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳,有 1/3 = 0.3333333333333333 的概率能够 1 秒 后跳到顶点 7 。
提示:
1 <= n <= 100edges.length == n - 1edges[i].length == 21 <= ai, bi <= n1 <= t <= 501 <= target <= n
class Solution {
//自底向上查找
public double frogPosition(int n, int[][] edges, int t, int target) {
List<Integer>[] g = new ArrayList[n + 1];
Arrays.setAll(g, e -> new ArrayList<>());
g[1].add(0);// 减少额外判断
for (var e : edges) {
int x = e[0], y = e[1];
g[x].add(y);
g[y].add(x); // 建树
}
long prod = dfs(g, target, 1, 0, t);
return prod != 0 ? 1.0 / prod : 0;
}
private long dfs(List<Integer>[] g, int target, int x, int father, int leftT) {
//t秒后在target
if (leftT == 0) {
return x == target ? 1 : 0;
}
//target是叶子停在原地
if (x == target) {
return g[x].size() == 1 ? 1 : 0;
}
for (int y : g[x]) {
if (y != father) {
long prod = dfs(g, target, y, x, leftT - 1);
if (prod != 0) {
return prod * (g[x].size() - 1);// 乘上儿子的个数
}
}
}
return 0;// 未找到 target
}
}
2646 最小化旅行的价格总和
参考题解:2646. 最小化旅行的价格总和 - 力扣(LeetCode)
现有一棵无向、无根的树,树中有 n 个节点,按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。
每个节点都关联一个价格。给你一个整数数组 price ,其中 price[i] 是第 i 个节点的价格。
给定路径的 价格总和 是该路径上所有节点的价格之和。
另给你一个二维整数数组 trips ,其中 trips[i] = [starti, endi] 表示您从节点 starti 开始第 i 次旅行,并通过任何你喜欢的路径前往节点 endi 。
在执行第一次旅行之前,你可以选择一些 非相邻节点 并将价格减半。
返回执行所有旅行的最小价格总和。
示例 1:
输入:n = 4, edges = [[0,1],[1,2],[1,3]], price = [2,2,10,6], trips = [[0,3],[2,1],[2,3]]
输出:23
解释:
上图表示将节点 2 视为根之后的树结构。第一个图表示初始树,第二个图表示选择节点 0 、2 和 3 并使其价格减半后的树。
第 1 次旅行,选择路径 [0,1,3] 。路径的价格总和为 1 + 2 + 3 = 6 。
第 2 次旅行,选择路径 [2,1] 。路径的价格总和为 2 + 5 = 7 。
第 3 次旅行,选择路径 [2,1,3] 。路径的价格总和为 5 + 2 + 3 = 10 。
所有旅行的价格总和为 6 + 7 + 10 = 23 。可以证明,23 是可以实现的最小答案。
示例 2:
输入:n = 2, edges = [[0,1]], price = [2,2], trips = [[0,0]]
输出:1
解释:
上图表示将节点 0 视为根之后的树结构。第一个图表示初始树,第二个图表示选择节点 0 并使其价格减半后的树。
第 1 次旅行,选择路径 [0] 。路径的价格总和为 1 。
所有旅行的价格总和为 1 。可以证明,1 是可以实现的最小答案。
提示:
1 <= n <= 50edges.length == n - 10 <= ai, bi <= n - 1edges表示一棵有效的树price.length == nprice[i]是一个偶数1 <= price[i] <= 10001 <= trips.length <= 1000 <= starti, endi <= n - 1
class Solution {
private List<Integer>[] g;
private int[] price, cnt;
private int end;
public int minimumTotalPrice(int n, int[][] edges, int[] price, int[][] trips) {
g = new ArrayList[n];
Arrays.setAll(g, e -> new ArrayList<>());
for (var e : edges) {
int x = e[0], y = e[1];
g[x].add(y);
g[y].add(x);
}
this.price = price;
cnt = new int[n];
for (var t : trips) {
end = t[1];
path(t[0], -1);
}
int[] p = dfs(0, -1);
return Math.min(p[0], p[1]);
}
private boolean path(int x, int father) {
if (x == end) {
cnt[x]++;//统计从start到end的路径上的点经过了多少次
return true;//找到终点
}
for (var y : g[x]) {
if (y != father && path(y, x)) {
cnt[x]++;
return true;
}
}
return false;//没找到终点
}
private int[] dfs(int x, int father) {
int notSelect = price[x] * cnt[x];//x不变
int select = notSelect / 2;//x减半
for (var y : g[x]) {
if (y != father) {
int[] p = dfs(y, x);//计算儿子y 不变/减半的最小价值总和
notSelect += Math.min(p[0], p[1]);
select += p[0];
}
}
return new int[]{notSelect, select};
}
}
2467 树上最大得分和路径
参考题解:2467. 树上最大得分和路径 - 力扣(LeetCode)
一个 n 个节点的无向树,节点编号为 0 到 n - 1 ,树的根结点是 0 号节点。给你一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] ,表示节点 ai 和 bi 在树中有一条边。
在每一个节点 i 处有一扇门。同时给你一个都是偶数的数组 amount ,其中 amount[i] 表示:
- 如果
amount[i]的值是负数,那么它表示打开节点i处门扣除的分数。 - 如果
amount[i]的值是正数,那么它表示打开节点i处门加上的分数。
游戏按照如下规则进行:
- 一开始,Alice 在节点
0处,Bob 在节点bob处。 - 每一秒钟,Alice 和 Bob 分别 移动到相邻的节点。Alice 朝着某个 叶子结点 移动,Bob 朝着节点
0移动。 - 对于他们之间路径上的每一个节点,Alice 和 Bob 要么打开门并扣分,要么打开门并加分。注意:
- 如果门 已经打开 (被另一个人打开),不会有额外加分也不会扣分。
- 如果 Alice 和 Bob 同时 到达一个节点,他们会共享这个节点的加分或者扣分。换言之,如果打开这扇门扣
c分,那么 Alice 和 Bob 分别扣c / 2分。如果这扇门的加分为c,那么他们分别加c / 2分。
- 如果 Alice 到达了一个叶子结点,她会停止移动。类似的,如果 Bob 到达了节点
0,他也会停止移动。注意这些事件互相 独立 ,不会影响另一方移动。
请你返回 Alice 朝最优叶子结点移动的 最大 净得分。
示例 1:
输入:edges = [[0,1],[1,2],[1,3],[3,4]], bob = 3, amount = [-2,4,2,-4,6]
输出:6
解释:
上图展示了输入给出的一棵树。游戏进行如下:
- Alice 一开始在节点 0 处,Bob 在节点 3 处。他们分别打开所在节点的门。
Alice 得分为 -2 。
- Alice 和 Bob 都移动到节点 1 。
因为他们同时到达这个节点,他们一起打开门并平分得分。
Alice 的得分变为 -2 + (4 / 2) = 0 。
- Alice 移动到节点 3 。因为 Bob 已经打开了这扇门,Alice 得分不变。
Bob 移动到节点 0 ,并停止移动。
- Alice 移动到节点 4 并打开这个节点的门,她得分变为 0 + 6 = 6 。
现在,Alice 和 Bob 都不能进行任何移动了,所以游戏结束。
Alice 无法得到更高分数。
示例 2:
输入:edges = [[0,1]], bob = 1, amount = [-7280,2350]
输出:-7280
解释:
Alice 按照路径 0->1 移动,同时 Bob 按照路径 1->0 移动。
所以 Alice 只打开节点 0 处的门,她的得分为 -7280 。
提示:
2 <= n <= 105edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedges表示一棵有效的树。1 <= bob < namount.length == namount[i]是范围[-104, 104]之间的一个 偶数 。
class Solution {
private int[] bobTime;
private int[] amount;
private int ans = Integer.MIN_VALUE;
public int mostProfitablePath(int[][] edges, int bob, int[] amount) {
int n = amount.length;
bobTime = new int[n];
Arrays.fill(bobTime, n);
this.amount = amount;
List<Integer>[] g = new ArrayList[n + 1];
Arrays.setAll(g, e -> new ArrayList<>());
for (var e : edges) {
int x = e[0], y = e[1];
g[x].add(y);
g[y].add(x); // 建树
}
dfsBob(g, bob, -1, 0);
g[0].add(-1);//防止把根节点当成叶子
dfsAlice(g, 0, -1, 0, 0);
return ans;
}
public boolean dfsBob(List<Integer>[] g, int p, int father, int time) {
if (p == 0) {
//到达0点
bobTime[p] = time;
return true;
} else {
boolean found0 = false;
for (int e : g[p]) {
if (e != father && dfsBob(g, e, p, time + 1)) {
found0 = true;
break;
}
}
if (found0) {
//到达0点
bobTime[p] = time;
}
return found0;
}
}
//total表示路径得分
public void dfsAlice(List<Integer>[] g, int p, int father, int time, int total) {
if (bobTime[p] == time) {
//两人相遇
total += amount[p] / 2;
}
if (bobTime[p] > time) {
total += amount[p];
}
//找到叶子结点 更新答案
if (g[p].size() == 1) {
ans = Math.max(ans, total);
return;
}
for (int e : g[p]) {
if (e != father) {
dfsAlice(g, e, p, time + 1, total);
}
}
}
}
968 监控二叉树
参考:树形 DP:监控二叉树【基础算法精讲 25】_哔哩哔哩_bilibili
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
输入:[0,0,null,0,0]
输出:1
解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
输入:[0,0,null,0,null,0,null,null,0]
输出:2
解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
- 给定树的节点数的范围是
[1, 1000]。 - 每个节点的值都是 0。
思路:
- 蓝色:安装摄像头
- 黄色:不安装摄像头,父节点安装摄像头
- 红色:不安装摄像头,至少一个儿子安装摄像头
蓝色=min(左蓝 左黄 左红)+min(右蓝 右黄 右红)+1
黄色=min(左蓝 左红)+min(右蓝 右红)
红色=min(左蓝+右红 左红+右蓝 左蓝+右蓝)
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int minCameraCover(TreeNode root) {
int[] res = dfs(root);
return Math.min(res[0], res[2]);
}
private int[] dfs(TreeNode root) {
if (root == null) {
return new int[]{Integer.MAX_VALUE / 2, 0, 0};
}
int[] left = dfs(root.left);
int[] right = dfs(root.right);
int choose = Math.min(Math.min(left[0], left[1]), left[2]) + Math.min(Math.min(right[0], right[1]), right[2]) + 1;
int byFather = Math.min(left[0], left[2]) + Math.min(right[0], right[2]);
int byChildren = Math.min(Math.min(left[0] + right[2], left[2] + right[0]), left[0] + right[0]);
return new int[]{choose, byFather, byChildren};
}
}
此外,我们发现红色的计算结果太多了(这一层有n个结点,总共有2^n-1种情况),那么我们该如何优化呢?
假设我们去掉必须选一个蓝色的条件,式子变为min(蓝1,红1)+min(蓝2,红2)+min(蓝3,红3)
例如,min(5,2)+min(7,6)+min(5,1),要想选择一个蓝色,必须将一个红色改为蓝色,因此将6改为7最为合适
由此,我们知道需要找到min(蓝-红),所以得到如下的式子:
黄色=min(蓝1,红1)+min(蓝2,红2)+min(蓝3,红3)
红色=黄色+max(0,min(蓝1-红2 蓝2-红2 蓝3-红3))
蓝色=min(蓝1 黄1)+min(蓝2 黄2)+min(蓝3 黄3)+cost[x]
cost[x]为花费的成本
蓝色一定大于红色,所以第三个蓝色的式子不用比较红色,这就是如下的题目
保安站岗(洛谷)
SDOI2006\ 保安站岗 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;
public class Main {
static int[] cost;
static List<Integer>[] g;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
cost = new int[n + 1];
g = new ArrayList[n + 1];
//建树
Arrays.setAll(g, e -> new ArrayList<>());
for (; n > 0; n--) {
int v = sc.nextInt();
v--;
cost[v] = sc.nextInt();
int m = sc.nextInt();
for (; m > 0; m--) {
int w = sc.nextInt();
w--;
g[v].add(w);
g[w].add(v);
}
}
int[] ans = dfs(0, -1);
int choose = ans[0];
int bySon = ans[2];
System.out.println(Math.min(choose, bySon));
}
static int[] dfs(int x, int father) {
int choose = cost[x];
int byFather = 0;
int minExtra = Integer.MAX_VALUE / 2;
for (var y : g[x]) {
if (y == father) {
continue;
}
int[] arr = dfs(y, x);
int c = arr[0];//蓝色
int byFa = arr[1];//黄色
int bySon = arr[2];//红色
choose += Math.min(c, byFa);
byFather += Math.min(c, bySon);
minExtra = Math.min(minExtra, c - bySon);
}
return new int[]{choose, byFather, byFather + Math.max(0, minExtra)};
}
}
LCP 34 二叉树染色
LCP 34. 二叉树染色 - 力扣(LeetCode)
小扣有一个根结点为 root 的二叉树模型,初始所有结点均为白色,可以用蓝色染料给模型结点染色,模型的每个结点有一个 val 价值。小扣出于美观考虑,希望最后二叉树上每个蓝色相连部分的结点个数不能超过 k 个,求所有染成蓝色的结点价值总和最大是多少?
示例 1:
输入:
root = [5,2,3,4], k = 2输出:
12
示例 2:
输入:
root = [4,1,3,9,null,null,2], k = 2输出:
16
提示:
1 <= k <= 101 <= val <= 100001 <= 结点数量 <= 10000
思路:
如果根节点是白色,那么返回左边的最大和和右边的最大和 即f[0]=maxleft+maxright
如果根节点是蓝色
当i=1时,两个儿子都为白色 此时f[i]=root.val+f[0](左)+f[0](右);
当i=2时,一个儿子为蓝色
- 如果k=2,可以分为 左 0 右 1、左 1 右 0 此时
f[i]=max(root.val+f[0](左)+f[1](右),root.val+f[1](左)+f[0](右)) - 如果k=3,可分为 左 0 右 2、左 1 右 1、左 2 右 0 三种情况;
最后得到 f[i]=max(val+f[j](左)+f[i-j-1](右))
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int maxValue(TreeNode root, int k) {
int[] ans = dfs(root, k);
int max = Integer.MIN_VALUE;
for (int a : ans) {
max = Math.max(max, a);
}
return max;
}
private int[] dfs(TreeNode root, int k) {
int[] f = new int[k + 1];
if (root == null) {
return f;
}
int[] left = dfs(root.left, k);
int[] right = dfs(root.right, k);
int maxLeft = Integer.MIN_VALUE;
int maxRight = Integer.MIN_VALUE;
for (int i = 0; i < k + 1; i++) {
maxLeft = Math.max(maxLeft, left[i]);
maxRight = Math.max(maxRight, right[i]);
}
f[0] = maxLeft + maxRight;
for (int i = 0; i < k + 1; i++) {
for (int j = 0; j < i; j++) {
f[i] = Math.max(f[i], root.val + left[j] + right[i - j - 1]);
}
}
return f;
}
}
LCP 64 二叉树灯饰
参考视频:动态规划 树形 DP【力扣杯2022秋·个人赛】_哔哩哔哩_bilibili
「力扣嘉年华」的中心广场放置了一个巨型的二叉树形状的装饰树。每个节点上均有一盏灯和三个开关。节点值为 0 表示灯处于「关闭」状态,节点值为 1 表示灯处于「开启」状态。每个节点上的三个开关各自功能如下:
- 开关
1:切换当前节点的灯的状态; - 开关
2:切换 以当前节点为根 的子树中,所有节点上的灯的状态; - 开关
3:切换 当前节点及其左右子节点(若存在的话) 上的灯的状态;
给定该装饰的初始状态 root,请返回最少需要操作多少次开关,可以关闭所有节点的灯。
示例 1:
输入:root = [1,1,0,null,null,null,1]
输出:2
解释:以下是最佳的方案之一,如图所示
示例 2:
输入:root = [1,1,1,1,null,null,1]
输出:1
解释:以下是最佳的方案,如图所示
示例 3:
输入:root = [0,null,0]
输出:0
解释:无需操作开关,当前所有节点上的灯均已关闭
提示:
1 <= 节点个数 <= 10^50 <= Node.val <= 1
思路:
任意一个结点,会受到哪些影响:
- 祖先结点的开关2的切换次数 偶数=不切换 奇数=切换
- 父节点是否切换了开关3
状态:(当前结点 开关2的切换次数的奇偶性 父节点是否开关3)
返回:当前状态,最少需要操作的次数
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
private HashMap<TreeNode, int[][]> map;
public int closeLampInTree(TreeNode root) {
map = new HashMap<>();
return dfs(root, false, false);
}
private int dfs(TreeNode root, boolean switch2_odd, boolean switch3) {
if (root == null) return 0;
//记忆化搜索
int x = switch2_odd ? 1 : 0;
int y = switch3 ? 1 : 0;
int[][] temp = new int[2][2];
if (map.containsKey(root)) {
temp = map.get(root);
if (temp[x][y] > 0) {
return temp[x][y];
}
} else {
map.put(root, temp);
}
int res = Integer.MAX_VALUE / 2;
//灯打开 开关2和开关3抵消 灯开
//灯关闭 开关2和开关3没有抵消 灯开
if ((root.val == 1) == (switch2_odd == switch3)) {
int res1 = dfs(root.left, switch2_odd, false) + dfs(root.right, switch2_odd, false) + 1;
int res2 = dfs(root.left, !switch2_odd, false) + dfs(root.right, !switch2_odd, false) + 1;
int res3 = dfs(root.left, switch2_odd, true) + dfs(root.right, switch2_odd, true) + 1;
int res123 = dfs(root.left, !switch2_odd, true) + dfs(root.right, !switch2_odd, true) + 3;
res = Math.min(Math.min(res1, res2), Math.min(res3, res123));
} else {
//灯关闭 不开开关 或者 开两个开关
int res0 = dfs(root.left, switch2_odd, false) + dfs(root.right, switch2_odd, false);
int res12 = dfs(root.left, !switch2_odd, false) + dfs(root.right, !switch2_odd, false) + 2;
int res13 = dfs(root.left, switch2_odd, true) + dfs(root.right, switch2_odd, true) + 2;
int res23 = dfs(root.left, !switch2_odd, true) + dfs(root.right, !switch2_odd, true) + 2;
res = Math.min(Math.min(res0, res12), Math.min(res13, res23));
}
temp[x][y] = res;
return res;
}
}