代码随想录算法训练营第35天 |(贪心-区间篇) 452. 用最少数量的箭引爆气球 435. 无重叠区间 763.划分字母区间 56.合并区间
代码随想录系列文章目录
贪心篇 - 区间问题
文章目录
- 代码随想录系列文章目录
- 452. 用最少数量的箭引爆气球
- 435. 无重叠区间
-
- 代码1(把这道题和452.用最少的箭引爆放在一起比较)
- 代码2
- 763.划分字母区间
- 56.合并区间
452. 用最少数量的箭引爆气球
题目链接
如何使用最少的弓箭呢?
直觉上来看,貌似只射重叠最多的气球,用的弓箭一定最少,那么有没有当前重叠了三个气球,我射两个,留下一个和后面的一起射这样弓箭用的更少的情况呢?
尝试一下举反例,发现没有这种情况。
局部最优:当气球出现重叠,一起射,所用弓箭最少。全局最优:把所有气球射爆所用弓箭最少。
思路确定下来,怎么去模拟实现这个过程呢?
1.为了让气球尽可能的重叠,需要对数组进行排序。
按照气球起始位置排序,还是按照气球终止位置排序呢?
其实都可以!只不过对应的遍历顺序不同,我就按照气球的起始位置排序了。
既然按照起始位置排序,那么就从前向后遍历气球数组,靠左尽可能让气球重复。
2.遍历每个小区间
从前向后遍历遇到重叠的气球了怎么办?
如果气球重叠了,重叠气球中右边边界的最小值 之前的区间一定需要一个弓箭。

可以看出首先第一组重叠气球,一定是需要一个箭,气球3,的左边界大于了 第一组重叠气球的最小右边界,所以再需要一支箭来射气球3了。
总结:我们可以将cnt 一开始初始化为1,表示肯定射第一组重叠气球,如果说,遍历第i个区间,区间左边界大于上一组重复区间的最小右边界的话,计数+1,然后维护当前组的最小右边界就行
class Solution:
def findMinArrowShots(self, points: List[List[int]]) -> int:
cnt = 1
points.sort(key = lambda x: x[0])
for i in range(1, len(points)):
if points[i][0] > points[i-1][1]: cnt += 1
else: points[i][1] = min(points[i][1], points[i-1][1])
return cnt
435. 无重叠区间
题目链接
代码1(把这道题和452.用最少的箭引爆放在一起比较)
如果说这道题是求无重叠的区间,上一道题452.可以说是尽可能让重叠的区间更多,只有迫不得已了才射下一只箭,也就是cnt+1。那其实,迫不得已射另一只箭,也说明区间无重复了,我们必须要拿另一只箭去射另一堆重叠区间了。
所以把上一题的代码改一改这道题就能过,只不过上一题为了尽可能重复,排序按照左端点排,这道题为了使右边有更多的区间,并且维护一个最小右边界,所以用右端点排序,最后求的是移除的个数,n-cnt

class Solution:
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
n = len(intervals)
intervals.sort(key = lambda x: x[1])
cnt = 1
for i in range(1, len(intervals)):
if intervals[i][0] >= intervals[i-1][1]:#这题的定义就算端点挨着也算不重叠
cnt += 1
else: intervals[i][1] = min(intervals[i-1][1], intervals[i][1])
return n-cnt
代码2
这道题应该说是比较难想的:
1.一看题就有感觉需要排序,但究竟怎么排序,按左边界排还是右边界排? 为什么按照右边界排序?排完序之后如何遍历?
右边界越小越好,只要右边界越小,留给下一个区间的空间就越大,所以从左向右遍历,优先选右边界小的。
这个也是这道题的思想精髓
接着分析,直接求重复的区间是复杂的,所以转而求最大非重复区间个数。然后这道题其实和452.有点像了,然后可以用452的思路求一下
也可以直接用下图思路:

区间,1,2,3,4,5,6都按照右边界排好序。
每次取非交叉区间的时候,都是可右边界最小的来做分割点(这样留给下一个区间的空间就越大),所以第一条分割线就是区间1结束的位置。
接下来就是找大于区间1结束位置的区间,是从区间4开始。意味着找到了第二堆区间,(和第一堆无重叠),然后这一堆的右边界更新为区间4的右边界,cnt+1
class Solution:
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
n = len(intervals)
intervals.sort(key = lambda x: x[1])
cnt = 1
right = intervals[0][1]
for i in range(1, len(intervals)):
if intervals[i][0] >= right:
right = intervals[i][1]
cnt += 1
return n-cnt
因为我们直接按照右边界排序的,我们最小右边界肯定是第一个数组,我们找到第二片不重叠的数组直接把它的右边界变成right。所以代码直接这样写。
763.划分字母区间
题目链接
这个划分区间,也是找一段类似字母无重复的区间
题目要求同一字母最多出现在一个片段中,那么如何把同一个字母的都圈在同一个区间里呢?
如果没有接触过这种题目的话,还挺有难度的。
在遍历的过程中相当于是要找每一个字母的边界,如果找到之前遍历过的所有字母的最远边界,说明这个边界就是分割点了。此时前面出现过所有字母,最远也就到这个边界了。
可以分为如下两步:
1.统计每一个字符最后出现的位置
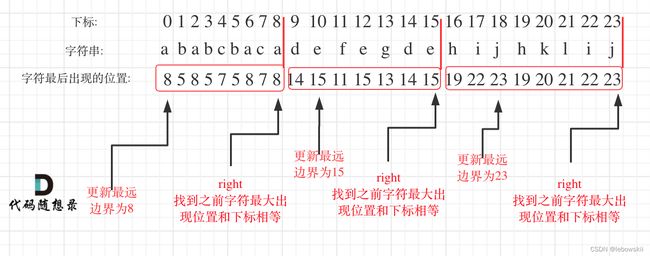
那怎么维护一个这样的,字符最后出现的位置呢?有26个字母,我们可以维护一个长度为26的数组,'a’的下标为0,值为最后一个a出现的位置,那么怎么维护呢?
ord(s[i])-ord(‘a’)就是把 a映射到下标0,z映射到下标25,遍历s,不断更新每一个字符出现的最远下标
dict = [0]*26
for i in range(len(s)):
dict[ord(s[i])-ord('a')] = i
2.从头遍历字符,并更新字符的最远出现下标,如果找到字符最远出现位置下标和当前下标相等了,则找到了分割点
class Solution:
def partitionLabels(self, s: str) -> List[int]:
dict = [0]*26
for i in range(len(s)):
dict[ord(s[i])-ord('a')] = i #把key固定到0-25, 然后value变成最远的位置下标, 即每个字母的最远下标维护成一个list
left, right = 0, 0
res = []
for i in range(len(s)):
right = max(right, dict[ord(s[i])-ord('a')])
if i == right:
res.append(right-left+1)
left = i+1
return res
56.合并区间
题目链接
其实这道题就是一个模拟题,我在八个月前刚开始做力扣的时候做过一次
这道题的思路比较好想,在做了上面几题之后,立马就模拟出了这道题的方法。
1.按照区间左端点排序
2.模拟的去合并区间,实际操作中,改变res内的上一个的右端点就行,取当前遍历到的区间和上一个的右端点长的(本身合并就该如此,有时候常识就是贪心,夺吓人)
写代码,善用切片,草,小米面试手撕给我挂了
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
intervals.sort(key = lambda x: x[0])
res = []
res.append(intervals[0])
for i in intervals[1:]:
if i[0] <= res[-1][1]:
res[-1][1] = max(res[-1][1],i[1])
else: res.append(i)
return res