动态规划之背包问题
前言:
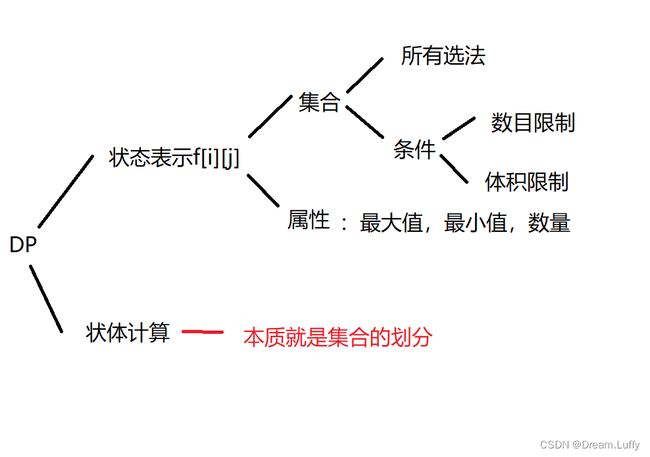
动态规划的本质,是对问题状态的定义和状态转移方程。
动态规划具备三个特点:
1.将原来的问题分解成几个相似的子问题;
2.所有的子问题都只需要解决一次
3.每个状态存储子问题的解
一般从三个角度考虑动态规划:
1.状态表示:
2.状态计算 - > 集合的划分
3.状态初始化
集合的划分依据,需要满足两个条件
1. 以最后一个改变的元素为依据。
2. 集合中应包含所有的方案。
而动态规划问题一般可以分为线性DP,背包问题,区间DP,计数类DP,数位统计DP,状态压缩DP,树形DP,背包问题是大头,也是我们这章的重点。
全文共12499字
目录:
一 .四个基础背包问题
①01背包
②完全背包
③多重背包
④分组背包
二 .背包问题的扩展
①二维背包
②混合背包
③背包求方案数
④背包存路径
⑤背包问题求方案数的至多、至少、恰好问题的总结
正文:
一.背包问题都以01背包为基础
我们以01背包问题为引子:
有 N 件物品和一个容量是 V 的背包。问最多能装入背包的总价值是多大?
状态表示:所有只从前i个物品中选, 总体积不超过j的方案集合;
集合划分:
初始化:第0行和第0列都为0,表示没有装物品时的价值都为0:F(0,j) = F(i,0) = 0;
对于集合的两种划分方式:
第一种方案:如果不选择第i个物品,价值就与前一维相同: f[i][ j] = f[i - 1][j]
第二种方案:不选择第i个物品: f[i][j] = f[i - 1][j - v[i]] + w[i]
从而得到状态转移方程,即max(f[i][j], f[i - 1][j - v[i]] + w[i] )
问题一:为什么方案二在这里第二维表示是j - v[i] ?
答:因为要选择的第i个物品体积为v[i] ,而总体积为j,所以要空出v[i]的体积来填充
二维c++代码如下:时间复杂度 :O(n * m )
注:具体题目可以在洛谷、力扣等平台找
#include
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main() {
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i]; //注意i要大于0,因为后面要用到下标i - 1;
for(int i = 1; i <= n; i++) {
for(int j = 0; j <= m; j++) {
if(j < v[i])f[i][j] = f[i-1][j];
else f[i][j] = max(f[i - 1][j], f[i-1][j-v[i]]+w[i]);
//最后即比较加上该物品时的价值与不加该物品时的价值哪个大,
//不加该物品时f[i][j]是指不包含该物品时其它相加的价值总和
//而加上此物品后,得到的是 f[i][j - v[i]] 的价值最大值加上当前物品价值w[i]
}
}
cout << f[n][m] << endl;
return 0;
}
为什么答案是f[n][m] ?
答:第一维是因为要枚举n个物品, 而第二维,即我们的背包体积,f[n][m] 是从f[1][0]一路推过来的。
一维优化: 时间复杂度 :O(n * m )
#include
#include
using namespace std;
const int N = 1010;
int n, m;//n是物品数量,m是背包最大容量
int v[N], w[N];//存储物品体积和价值
int f[N];//存储最优解答
int main()
{
cin >> n >> m;
//输入对应的 体积和价值
for(int i = 1;i <= n;i ++) cin >> v[i] >>w[i];
for(int i =1;i <= n;i ++)
for(int j = m;j >= v[i];j --)//如果正序枚举,j循环中的小体积的更新更新会 影响后面的更新
f[j] = max(f[j], f[j - v[i]] + w[i]);//因为f[j - v[i]] + w[i]这里用的 f[j - w[i]
//应该是上一层i的,即i - 1而不能在这层之前被更新,否则会影响到后面更新
cout << f[m] << endl;
return 0;
}
这里存在两个问题:
一. 为什么可以这样优化
我们可以注意到二维数组的更新方式为
f[i][j] = f[i - 1][j] // 不含i的所有选法的最大价值
if j >= v[i] //判断含i的选法是否成立
f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i])
可以看出,f[i][] 只与f[i - 1]相关,所以根本没必要保留f[i - 2]即后面的状态值。
将空间从O(n*m)优化为 O(m), n, m分别为物品个数和背包体积。
二. 为什么第二行循环需要倒叙枚举 (与之相对的是完全背包的正序枚举)
当我们更新索引值较大的dp值时,需要用到索引值较小的上一层dp值dp[j - v[i]];
也就是说,在更新索引值较大的dp值之前,索引值较小的上一层dp值必须还在,还没被更新;
所以只能索引从大到小更新。
就是说 在状态转移方程f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i])中f[i - 1][j - v[i]] 这里使用的是i - 1层的dp,而如果我们正向枚举时 我们的 f[ j - v[i] ]会在 f[j] 之前更新,也就是在更新到f[j - v[i]]这一层时,我们使用的将是被更新过的 f[i][j - v[i]] ,这与原方程f[i - 1][j - v[i]] 不同,所以我们需要倒叙枚举,使得我们将使用的f[j - v[i]] 是未被更新过的
二.有了以上的基础,我们就可以展开对 完全背包,多重背包, 分组背包, 这三个基础背包模型的学习
完全背包 :有 N种物品和一个容量是 V 的背包,每种物品都有无限件可用。
状态表示: 所有只从前i个物品中选, 总体积不超过j的方案集合
集合的划分方式:第i个物品选几个
状态转移方程由集合的划分方式可得max(f[i ][j], f[i - 1][j - k * v[i]] + k * w[i] )
二维代码如下:时间复杂度 :O(n * m )
#include
using namespace std;
const int N = 1010;
int f[N][N];
int v[N],w[N];
int main()
{
int n,m;
cin>>n>>m;
for(int i = 1 ; i <= n ;i ++)
{
cin>>v[i]>>w[i];
}
for(int i = 1 ; i<=n ;i++)
for(int j = 0 ; j<=m ;j++)
{
for(int k = 0 ; k*v[i]<=j ; k++)
f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
}
cout< 这里多了一层循环,用于枚举决策,而我们一般的循环次序就如此:物品个数 -> 体积 -> 决策。
这里,我们列举一下更新次序的内部关系,可以发现优化方式:
f[i , j ] = max( f[i-1,j] , f[i-1,j-v]+w , f[i-1,j-2*v]+2*w , f[i-1,j-3*v]+3*w , .....)
f[i , j-v]= max( f[i-1,j-v] , f[i-1,j-2*v] + w , f[i-1,j-3*v]+2*w , .....)
由上两式,可得出如下递推关系:
f[i][j]=max(f[i,j-v]+w , f[i-1][j])
得到了以上的关系,我们可以发现,第三重循环k可以舍去了
于是得到优化的一维代码:时间复杂度 :O(n * m )
#include
#include
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
cin >> n >> m;
for(int i = 1;i <= n;i ++) cin >> v[i] >> w[i];
for(int i = 1;i <= n;i ++)
for(int j = v[i];j <= m;j ++)//因为完全背包 使用当前行的状态更新,
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
}
这里,我们是正序枚举的,因为从前面得到的递推公式中我们可以发现 f[i][j] = max(f[i][j],f[i][j - v]); 这里使用的都是第i层dp,故不用倒叙枚举,而在背包中,只有完全背包是正序枚举的。
多重背包:有 N种物品和一个容量是 V 的背包,每种物品都有s[i]件 (01背包 和完全背包 可以看作多重背包的特殊情况)
状态表示:所有只从前i个物品中选, 总体积不超过j的方案集合
集合划分方式与完全背包一样
状态转移方程由集合的划分方式可得max(f[i ][j], f[i - 1][j - k * v[i]] + k * w[i] )
优化前代码如下: 时间复杂度:O(n∗v∗s))
#include
#include
using namespace std;
const int N = 110; //数据量小可以朴素做法
int n, m;
int v[N], w[N], s[N];//s[n]存储物品个数
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1;i <= n;i ++) cin >> v[i] >> w[i] >> s[i];
for(int i = 1;i <= n;i ++)
for(int j = 0;j <= m;j ++)
for(int k = 0;k <= s[i] && k * v[i] <= j;k ++)
f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] +w[i] *k);//当k=0时就包括了f[i - 1][j],相当于对f[i][j]赋值
cout << f[n][m] << endl;
return 0;
}
但是要注意到这不能像完全背包一样优化,我们一样可以观察这两个状态转移方程
f[i , j ] = max( f[i-1,j] , f[i-1,j-v]+w , f[i-1,j-2*v]+2*w , f[i-1,j-3*v]+3*w , .... , f[i-1,j-s[i]*v]+s[i]*w )
f[i , j-v]= max( f[i-1,j-v] , f[i-1,j-2*v] + w , f[i-1,j-3*v]+2*w , ....., f[i-1,j-s[i]*v]+s[i]*w ,f[i-1,j - (s[i] + 1)*v]+ s[i] *w );
我们可以发现后面多了一项,这是为什么? 因为s[i]是相同的 前面往后挪了一项,后面也要挪一项。
那么这里可以像完全背包那样优化吗?
答案是不能的,因为我们无法在知道 (f[i-1,j-v] , f[i-1,j-2*v] + w , f[i-1,j-3*v]+2*w , ....., f[i-1,j-s[i]*v]+s[i]*w ,f[i-1,j - (s[i] + 1)*v]+ s[i] *w ); 的最大值的情况下,
得到 (f[i-1,j-v] , f[i-1,j-2*v] + w , f[i-1,j-3*v]+2*w , ....., f[i-1,j-s[i]*v]+s[i]*w) 的最大值。
因为当 f[i-1,j - (s[i] + 1)*v]+ s[i] *w 与前面一个值相等时,我们就无法得到最大值, 所以我们只能放弃原有的优化方式, 而采用全新的,二进制优化方式。
优化后代码: 时间复杂度:(n * v * log s)
#include
#include
using namespace std;
const int N = 12010, M = 2010;
int n, m;
int v[N], w[N];
int f[M];
int main()
{
cin >> n >> m;
int cnt = 0;
for(int i = 1;i <= n;i ++)//拆分打包
{
int a, b, s; //体积,价值,数量
cin >> a >> b >> s;
int k = 1;
while( k <= s)
{
cnt ++;
v[cnt] = a * k;
w[cnt] = b * k;
s -= k;
k *= 2;//以二进制优化
}
if(s > 0)//如果有多
{
cnt ++;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
for(int i = 1;i <= cnt;i ++)//以一重背包的形式枚举
{
for(int j = m;j >= v[i];j --)
{
f[j] = max(f[j],f[j - v[i]] + w[i]);
}
}
cout << f[m] << endl;
return 0;
}
什么? 你说二进制优化凭什么正确?
这里,我们将每一个体积及价值拆分成 二进制形式,然后将每一个打包成的体积,进行一次01背包即可,
在这里,我们可以假设物品一体积为7 ,那么我们可以将其拆分为1, 2, 4;
而我们知道01背包是枚举每个物品是否需要取,也就是对这些被拆分的体积进行组合,可以得到1 ,2 ,3 , 4, 5, 6, 7每一个体积, 所以可以进行二进制枚举。
当然也有更高效的单调队列优化方式,平时不常用到,这里就不一一例举。
分组背包 :
有 N 组物品和一个容量是 V 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
状态表示:所有只从前i组物品中选, 总体积不超过j的方案集合
分组背包的本质:每个组中的决策都是互斥的
状态转移方程由集合的划分方式可得max(f[j], f[j - v[i][k]] + w[i][k]);
废话不多说,直接上代码(如何不知道一维是怎么优化来的,再回顾上面的内容,后面不再赘述)
#include
#include
using namespace std;
const int N = 110;
int f[N], v[N][N], w[N][N], s[N];
int main()
{
int n , m;
cin >> n >> m;
for(int i = 1;i <= n;i ++)//有n个小组
{
cin >> s[i];
for(int j = 0;j < s[i]; j ++)
cin >>v[i][j] >> w[i][j];
}
for(int i = 1;i <= n;i ++)
for(int j = m;j >= 0;j --)
for(int k = 0;k < s[i];k ++)//枚举所有选择
if(v[i][k] <= j)
f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
cout << f[m] << endl; //f[j]为不选,后者为选
}
好了,结束了,跑路咯....啥?嫌少?那就把你狠狠地小扩展一下!
第一个扩展:二维费用的背包问题
有 NN 件物品和一个容量是 V的背包,背包能承受的最大重量是 M。
每件物品只能用一次。体积是 vi,重量是 mi,价值是 wi。
这里,有两个限制条件,也即有两个体积,只需多加一层循环,做一遍01背包即可
我是代码:
#include
using namespace std;
const int N = 110;
int n, V,M; //V和M为两维费用
int f[N][N];
int main()
{
cin >> n >> V >> M;
for(int i = 0;i < n;i ++)
{
int v, m, w;
cin >> v>> m >> w;
for(int j = V; j >= v;j --)
for(int k = M;k >= m;k --)
f[j][k] = max(f[j][k] , f[j - v][k - m] + w);
}
cout << f[V][M] << endl;
return 0;
} 不过瘾?
第二个扩展: 不如整个混合背包
有 N 种物品和一个容量是 V 的背包。
物品一共有三类:
- 第一类物品只能用1次(01背包);
- 第二类物品可以用无限次(完全背包);
- 第三类物品最多只能用 si 次(多重背包);
每种体积是 vi,价值是 wi。
输入:
-
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行三个整数 vi,wi,si,用空格隔开,分别表示第 ii 种物品的体积、价值和数量。
- si=−1 表示第 i 种物品只能用1次;
- si=0表示第 i 种物品可以用无限次;
- si>0 表示第 i 种物品可以使用 si 次;
芜湖,这咋搞??
还记得我们在前面提到的吗?
01背包和完全背包,是多重背包的特殊形式
于是我们就有了以下两种想法:
1.把01背包并入多重背包计算, 完全背包单独计算
2.因为体积限定,以有完全背包实际上并不能取无限个物品i,故我们可以将完全背包某个物品的上限记为 总体积m / 物品体积v[i] , 那么我们可以同时将01背包和完全背包纳入多重背包中计算。
以下对多重背包的计算会采用二进制优化,以回顾前面内容
方法一隆重登场: 这里直接将二进制融入了循环中
//解法一,将01背包看为多重背包
#include
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N], s[N];
int f[N];
int main()
{
cin >>n >> m;
for(int i = 1;i <= n;i ++) cin >> v[i] >> w[i] >> s[i];
for(int i = 1;i <= n;i ++)
{
if(!s[i]) //完全背包
{
for(int j = v[i];j <= m;j ++)
{
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}
else
{
//将多重背包利用二进制枚举优化
//将01背包融入多重背包中
if(s[i] == -1) s[i] = 1;
for(int k = 1;k <= s[i];k *= 2)//二进制优化枚举
{
for(int j = m;j >= k * v[i]; j --)
{
f[j] = max(f[j], f[j - k * v[i]] + k * w[i]);
}
s[i] -= k;
}
if(s[i])//若s[i]还没减完
{
for(int j = m;j >= s[i] * v[i];j --)
{
f[j] = max(f[j], f[j - s[i] * v[i]] + s[i] * w[i]);
}
}
}
}
cout << f[m] << endl;
}
方法二隆重登场:
//解法二,将完全背包也看为多重背包问题
#include
using namespace std;
const int N = 100010; //范围要开大,因为要用二进制优化
int n, m, v[N], w[N], f[N];
int main()
{
cin >>n >> m;
int cnt = 1;
for(int i = 1;i <= n;i ++)
{
int a, b ,s;
cin >>a >> b >> s;
int k = 1;
if(s < 0) s = 1;
else if(s == 0) s = m/a;//把01背包和多重背包先转化成多重背包,若为完全背包,则在最优情况下,只能取总体积/该物品体积向下取整
while(k <= s)
{
v[cnt] = a * k;
w[cnt] = b * k;
s -= k;
k *= 2;
cnt ++;
}
if(s > 0)
{
v[cnt] = s * a;
w[cnt] = s * b;
cnt ++;
}
} //将多重背包进行二进制优化,变成01背包
for(int i = 1;i <= cnt;i ++)
{
for(int j = m;j >= v[i];j --)
{
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}
cout << f[m] << endl;
}
方法二的第一种二进制表达方式:
#include
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N], s[N], f[N];
int main()
{
cin >>n >> m;
for(int i = 1;i <= n;i ++ ) cin >> v[i] >> w[i] >> s[i];
for(int i = 1;i <= n;i ++)
{
if(!s[i])
s[i] = m / v[i]; //完全背包
else if(s[i] == -1)
s[i] = 1;
//二进制优化
for(int k = 1;k <= s[i];k *= 2)
{
for(int j = m;j >= k * v[i];j --)
{
f[j] = max(f[j], f[j - k * v[i]] + k * w[i]);
}
s[i] -= k;
}
if(s[i] > 0)
{
for(int j = m; j >= s[i] * v[i];j --)
{
f[j] = max(f[j], f[j - s[i] * v[i]] + s[i] * w[i]);
}
}
}
cout << f[m];
return 0;
}
再来再来!
第三个扩展: 数字组合
给定 N 个正整数 A1,A2,…,AN,从中选出若干个数,使它们的和为 M,求有多少种选择方案。
第一行包含两个整数 N 和 M。
第二行包含 NN 个整数,表示A1,A2,…,AN。
求方案数是什么玩意???
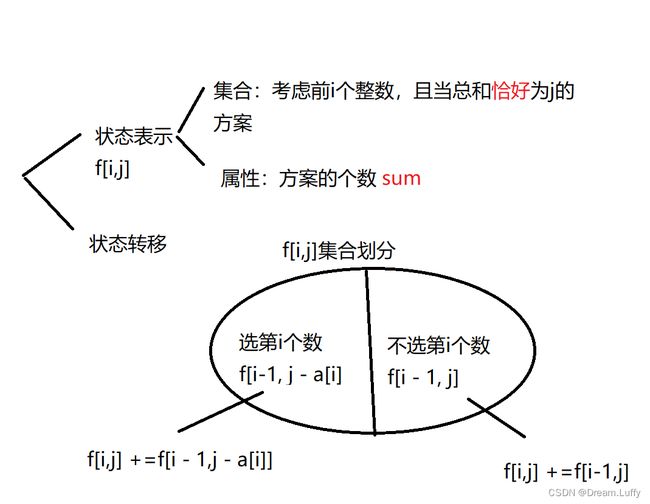
这里,我们可以发现两个和之前不同的地方,
①限制条件由原来的体积不超过M,变为 体积(若干个数)和恰好为M。
②答案由给定体积求最大价值,变为求方案数。
写题不能靠瞎想,我们画个图康康
也就是说,选i和不选i 都是能得到当前总和j 的方法咯 ,既然两条路都行,那就把它们都加起来吧!
于是,我们不就得到了状态转移方程了吗
f[ i , j ] = f[ i - 1 , j ] + f[ i - 1 , j - v[ i ] ]
优化为一维:f[j] += f[j - v[i]];
等等,这个恰好有啥用? 正是由这个条件,我们初始化时可以发现 f[0][0] = 1 (记住这个恰好哦,后面还有至多,至少,恰好的总结)
为啥? 因为当个数为0,体积为0时也是一种选法 soga!
直接上代码!
#include
using namespace std;
const int N = 110, M = 10010;
int n, m;
int v[N];
int f[M];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; ++ i) cin >> v[i];
f[0] = 1;
for (int i = 1; i <= n; ++ i)
{
for (int j = m; j >= v[i]; -- j)
{
f[j] += f[j - v[i]];
}
}
cout << f[m] << endl;
return 0;
啊这,为啥f[0] = 1啊? 因为当物品数为0时,体积大于0都不是合法方案如f[0][1],f[0][2]...f[0][j] , 只有f[0][0]是合法方案都没有体积你想塞啥进去(¬︿̫̿¬☆)
第四个扩展: 潜水员问题,求最小值(至少的问题)
算法分析:
这里就不画图了哈。。懒癌附身
状态表示:f[i,j,k] 所有从前i个物品中选,且氧气含量至少是j, 氮气含量至少是k的所有选法的气缸重量总和的最小值
状态计算:
所有不包含物品i的所有选法:f[i - 1,j,k]
所有包含物品i的所有选法:f[i - 1,j - v1,k - v2]
这里需要注意的是,所需的氧气或者氮气的数量如果是负数,它与数量为0是等价的。
为什么呢?例如f[5][10] 至少需要5氧气,10氮气, 求能拿到价值的最小值,而现在只有一个物品,氧气是6,氮气是7价值w,该物品是可以被携带的,因为它说至少需要5氧气,那么氧气6还是可以用到的,只是多1个氧气占着没用而已,因此,若用了这个物品,则变成了求 f[0][1] + w 表示氧气已经不再需要了。
也就是说, f[5][10]是可以由f[-1][3]更新过来的, 所以在 至少 这个前提下,体积是可以小于0的
由此我们可以得到状态转移方程:
for(int j = V;j >= 0;j --)
for(int k = M;k >= 0;k --) //注意这里是大于等于0
f[j][k] = min(f[j][k], f[max(0, j - v)][max(0, k - m)] + w); // 体积小于0与0等价,但下标不能小于0
给出代码:
#include
#include
#include
using namespace std;
const int N = 22, M = 80;
int n, m, K;
int f[N][M];
int main()
{
cin >>n >> m >> K;
memset(f, 0x3f, sizeof f); //因为要求的是最小值,初始化为正无穷是为了在更新时不使用它
f[0][0] = 0;
while(K --)
{
int v1, v2, w;
cin >> v1 >> v2 >> w;
for(int i = n;i >= 0;i --) //j可以小于v,因为求得是至少
for(int j = m;j >= 0; j --)
f[i][j] = min(f[i][j], f[max(0, i - v1)][max(0, j - v2)] + w);
}
cout << f[n][m];
return 0;
} 第五个扩展: 背包问题记录方案路径
算法分析:
题目要求输出字典序最小的解,假设存在最优解包含第一个物品,为了确保字典序最小那么我们必然选第一个。
于是问题就转化成从2~N这些物品中寻找最优解。因为我们要得到的是字典序最小的答案,所以状态定义也与之前有所不同。
在前面,我们的f[i,j] 记录的都是前i个物品总容量为j的最优解,那么现在我们将f[i,j] 定义为从第i 个元素到最后一个元素总容量为j的最优解。于是我们可以得到新的状态转移方程
f[i , j] = max( f[i + 1, j] , f[i + 1, j - v[i]] + w[i] );
由此,f[1][m] 是最大价值,由状态转移方程,我们可以发现 有三种情况
如果f[i, m] == f[i + 1, m - v[i]] + w[i] ] 说明选取了第i个物品可以得到最优解
如果f[i, m] == f[i+ 1, m], 说明不选取第i个物品才能得到最优解
如果 f[i, m] == f[i + 1, m - v[i]] + w[i] ] == f[i+ 1, m], 说明两种情况选与不选都可以得到最优解,但是由于我们要得到字典序最小的答案,故我们也需要选取这个物品
需要注意的一个不同点是,这里第一次循环需要逆序枚举,由我们的状态转移方程可以得到
//求具体方案数需要逆向枚举,此时f[1][m]为最优解,再由1~n枚举,从后往前得到具体路径。
#include
using namespace std;
const int N = 1010;
int n, m;
int w[N],v[N];
int f[N][N];
int main()
{
cin >>n >> m;
for(int i = 1;i <= n;i ++) cin >> v[i] >> w[i];
for(int i = n;i >= 1;i --)
for(int j = 0;j <= m;j ++)
{
f[i][j] = f[i + 1][j];
if(j >= v[i]) f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
}
int j = m;
for(int i = 1;i <= n;i ++)
if(j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i])
{
cout << i << " ";
j -= v[i];
}
return 0;
} 如果题目没有要求字典序最小时,我们就不用改变原有的状态转移方程,只需在寻找答案时逆序枚举即可。
第六个扩展: 背包问题求方案数
这里直接上代码了
//f[i][j]表示从前i个物品中选择,体积就是j的价值,g[i][j]表示表示从前i个物品种选择
//体积就是j的最大价值对应方案数
#include
#include
#include
using namespace std;
const int N=1010,mod=1e9+7;
int f[N],g[N];
int main()
{
int n,m;
cin>>n>>m;
memset(f,-0x3f,sizeof f);
f[0]=0,g[0]=1;//显然选体积为0价值为0,而什么都不选的选法为1
int mt=0;//用于保存最大值
for(int i=1;i<=n;i++)
{
int v,w;
cin>>v>>w;
for(int j=m;j>=v;j--)
{
int maxv=max(f[j],f[j-v]+w);
int s=0;//s这个临时变量存储的是能递推过来的最大价值的方案数
if(maxv==f[j]) s+=g[j];//当maxv==f[j]时,说明最大价值可由上一层递推过来
//那么s就需要加上上一层的方案数
if(maxv==f[j-v]+w) s=(s+g[j-v])%mod;//当maxv==f[j-v]+w时,说明最大价值可由本层递推过来
//那么s就需要加上本层的方案数
f[j]=maxv,g[j]=s;//最终体积为j的对应的最大价值的方案数便为s
mt=max(mt,maxv);
}
}
int res=0;
for(int i=1;i<=m;i++)//mt就是最大价值
if(f[i]==mt) res=(res+g[i])%mod;
cout<< max(res, 1) < 第七个扩展: 背包问题方案数总结
求方案数初始化总结
二维情况
1、体积至多j,f[0][i] = 1, 0 <= i <= m,其余是0 //因为体积至多是j, 假设体积是5,那么体积为0 也满足了条件,所以每种方案都有一种
2、体积恰好j,f[0][0] = 1, 其余是0 //同理,体积为j时,物品数为0不合法
3、体积至少j,f[0][0] = 1,其余是0 //同上,假设体积至少为5,不合法
一维情况
1、体积至多j,f[i] = 1, 0 <= i <= m,
2、体积恰好j,f[0] = 1, 其余是0
3、体积至少j,f[0] = 1,其余是0
求最大值最小值初始化总结
二维情况
1、体积至多j,f[i,k] = 0,0 <= i <= n, 0 <= k <= m(只会求价值的最大值)
2、体积恰好j,
当求价值的最小值:f[0][0] = 0, 其余是INF
当求价值的最大值:f[0][0] = 0, 其余是-INF
3、体积至少j,f[0][0] = 0,其余是INF(只会求价值的最小值)
一维情况
1、体积至多j,f[i] = 0, 0 <= i <= m(只会求价值的最大值)
2、体积恰好j,
当求价值的最小值:f[0] = 0, 其余是INF
当求价值的最大值:f[0] = 0, 其余是-INF
3、体积至少j,f[0] = 0,其余是INF(只会求价值的最小值)
//但是在至少的情况下,对体积的枚举不同,可以允许v > j, 因为体积为-2时,也满足了至少为0这一条件
这里给出两个求至少情况的代码作参考:
求方案数时:
#include
using namespace std;
const int N = 110;
int n, m;
int f[N][N];
int main()
{
cin >> n >> m;
f[0][0] = 1;
for(int i = 1;i <= n;i ++)
{
int v;
cin >> v;
for(int j = 0;j <= m;j ++)//即使物品体积比j大,j - v < 0,也能选,等价于f[i - 1][0]
{
f[i][j] = f[i - 1][j] + f[i - 1][max(0,j - v)];
}
}
cout << f[n][m] << endl;
return 0;
}
求价值时:
#include
#include
using namespace std;
const int N = 110, INF = 0x3f3f3f3f;
int n, m;
int f[N][N];
int main()
{
cin >> n >> m;
memset(f, INF, sizeof f);
f[0][0] = 0;
for(int i = 1;i <= n;i ++)
{
int v, w;
cin >> v >> w;
for(int j = 0;j <= m;j ++)
{
f[i][j] = min(f[i - 1][j], f[i][max(0, j - v)] + w);//即使物品体积比j大,j - v < 0,也能选,等价于f[i - 1][0]
}
}
cout << f[n][m] << endl;
return 0;
}
心中无女人,coding自然神
下班下班,有空再更。