leetcode 每日一题复盘(10.9~10.15)

leetcode 101 对称二叉树 

这道题一开始想是用层序遍历,看每一层是否都对称,遇到一个问题就是空指针(子树为空)无法记录下来,同时会导致操作空指针的问题,因此需要修改入队条件,并用一个标志去表示空指针

            vectornumv;
            for(int i=0;ival);
                if(!front)numv.emplace_back(-101);
                if(front)que.push(front->left);
                if(front)que.push(front->right);
            }

修改后入队条件不再是看入队元素是否为空,而是看队列中的元素是否为空,这样就可以将空指针也入队同时解决操作空指针的问题,如果指针为空,那么用-101标志他(子树的值范围是-100~100)

这样修改过后运行效率还可以,但是并没有完成理解这道题

正确的解法是用类似层序遍历但不是层序遍历的思想,将左子树的左孩子和右子树的右孩子比较(外侧),将左子树的右孩子和右子树的左孩子比较(内侧),每一层(除第一层)都比较内外侧,如果不同就false,每次出队两个元素

树可以分成3种情况,都无孩子,一个孩子,和两个孩子

两个孩子则比较大小,一个孩子直接false,都无孩子即位置对称,继续下次循环

leetcode 257 二叉树的所有路径

 能想到是前序遍历，但是对回溯还不太熟悉，没有想到用数组或者栈去存放每个节点的值，用这样一个数据结构去存放数据，是方便到时候进行回溯

递归

需要回溯自然而然会想到递归，做递归最难的地方在于弄清楚流程，思维容易混乱

首先我们可以确定递归的结束条件:找到叶子节点。找到叶子节点后，我们应该怎么处理叶子节点，这就是需要我们设计的代码部分

然后我们确定递归所需要的参数:二叉树的指针node（用于遍历查找叶子节点），int类型的数组path（用于存放数据的值，方便后面进行回溯！这个对初学者并不容易想到），string类型的数组res（用于存放路径）

最后我们就要设计递归函数的代码部分了:已知我们有一部分是处理找到叶子节点的情况，与之相反我们要设计没有找到叶子节点的情况

找到叶子节点的情况，这个时候我们应该将数组path的值取下来（注意要进行数据类型转换），并插入到res数组中，结束后return结束本次递归

没有找到叶子节点的情况，就需要继续往下递归，分别往左子树右子树进行递归，注意需要进行回溯操作！这个是回溯算法的精髓！如果左子树不回溯，右子树进行递归是path的数据将出错

 字丑勿怪，大致的思路流程就是这样

迭代

迭代法本质上也是回溯，这里就用栈来存放数据的值，构造一个类似节点栈的镜像栈

与用数组存放不同，数组里全部数据是一条路径，而栈的最后一个元素是一条路径，栈将路径的每一种状态都存进栈中

在没找到叶子节点时，先处理右子树还是先处理左子树没有区别，只是进入res的顺序不同

leetcode 404 左叶子之和 

记录一下第一次完全自己写出来的递归,一次就ac了,这题可以作为设计递归的思路样板

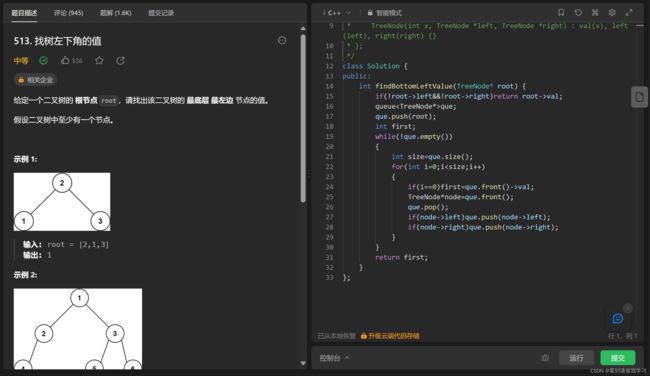
leetcode 513 找树左下角的值 

这题用层序遍历很容易,这里讲一下递归的方法

求最后一层的节点,我们可以把其看作求最大深度,用求最大深度的角度去做 

class Solution {
public:
    int maxDepth = INT_MIN;//记录最大层数
    int result;//result记录最后一层的最左节点的值
    void traversal(TreeNode* root, int depth) {
        if (root->left == NULL && root->right == NULL) {
            if (depth > maxDepth) {
                maxDepth = depth;
                result = root->val;
            }
            return;
        }//处理叶子节点,更新result,maxdepth的值
        if (root->left) {
            depth++;
            traversal(root->left, depth);
            depth--; // 回溯
        }//必须先处理左子树!不然将记录最右节点的值
        if (root->right) {
            depth++;
            traversal(root->right, depth);
            depth--; // 回溯
        }
        return;
    }
    int findBottomLeftValue(TreeNode* root) {
        traversal(root, 0);
        return result;
    }
};

注意递归时需要回溯!不然右子树递归时depth会多1

至于什么时候需要回溯,这需要根据你设计的算法和需求决定,这里是中左右遍历,涉及到depth的值变化,需要回到中节点再递归右子树因此需要回溯

leetcode 112 路径总和

一开始自己也写了一个void类型的递归算法,但是结果效率并不高,对递归的原理还是没有透彻,做完这题和113那题之后有了新的理解

这里截取一下卡哥的文章:

判断是否有这么一条路径,需要返回truefalse就一定需要返回值(如果没有返回值就需要用全局变量去记录结果,我用的就是这种方法)

查找路径,我们通常用数组或者栈去记录路径,这是常规的做法,这题只需要返回bool因此不用记录路径(当然你也可以记录路径,不过很麻烦),用count记录路径之和与target的差即可

涉及到bool类型的递归,这里一个return true那里一个return false很容易把人搞晕,下面我仔细讲一讲涉及bool的递归

涉及bool返回值的递归的关键在于，下层递归的返回值是判断上层返回值的依据

if（traverse（...）[下一层递归的返回值]）return true;

如果最后一层是true，整个函数返回值都是true

最后一层递归的返回值决定上层返回值，从而决定整个函数的返回值

返回值类型为int的递归也是如此，最后一层的返回值可以给到上一层递归使用（当然你也可以不用，看你如何设计）这反应了一种自底向上的思想

举例:可以用这种思想统计树中每一个节点的值之和，如果不是叶子节点就继续递归，返回本节点的值加上递归;叶子节点时则返回叶子节点的值

一层一层调用函数递，再从下层返回将值归到最外层

leetcode 105 从前序与中序遍历序列构造二叉树 

这题我明白他的构造过程,但是转换成编程语言的时候却一点头绪没有,想不出来应该怎么切割,后来看了题解才明白

大概思路是先把先序数组的第一个数取出来,当作树的根节点(因为是先序遍历,第一个元素必是整个树的总根) ,然后我们在中序数组中找到这个元素并返回其下标,作为切割的分界点,根据这个分界点,我们将中序数组分成左右两个数组(即左右子树),然后根据这两个数组将前序数组也分成左右数组,这四个数组就是下一次递归的参数,如此反复递归直到前序数组的大小为一时不再递归(前序数组每处理完一个节点就会删除掉他)

但是这种做法非常耗费时间和空间,因此需要想办法减少构造数组

 TreeNode*traverse(vector& preorder,int preorderbegin,int preorderend,vector& inorder,int inorderbegin,int inorderend)
    {
        if(preorderbegin==preorderend)return nullptr;//前序数组为空
        TreeNode*node=new TreeNode(preorder[preorderbegin]);//不能为0,因为我们没有删除前序数组,只是用索引
        if(preorderend-preorderbegin==1)return node;
        int mid;
        for(mid=inorderbegin;midval)break;
        }
       //遵循左闭右开原则
        int leftinorderbegin=inorderbegin;中序列的左子树的头
        int leftinorderend=mid;//中序列的左子树的尾,尾是取不到的所以是mid
        int rightinorderbegin=mid+1;;//中序列的右子树的头
        int rightinorderend=inorderend;//中序列的右子树的尾
//将原来的四个数组变为整数,一头一尾一共有八个整数
        int leftpreorderbegin=preorderbegin+1;//前序列的左子树的头,根在左子树前因此+1,下面的右子树就不用+1了
        int leftpreorderend=preorderbegin+1+mid-inorderbegin;//mid-inorderbegin是左子树的长度
        int rightpreorderbegin=preorderbegin+1+mid-inorderbegin;
        int rightpreorderend=preorderend;

        node->left=traverse(preorder,leftpreorderbegin,leftpreorderend,inorder,leftinorderbegin,leftinorderend);
        node->right=traverse(preorder,rightpreorderbegin,rightpreorderend,inorder,rightinorderbegin,rightinorderend);
        return node;
    }
    TreeNode* buildTree(vector& preorder, vector& inorder) {
        return traverse(preorder,0,preorder.size(),inorder,0,inorder.size());
    }

写了详细的注释,106的后序遍历中序遍历构造树也是类似的做法,前序后序是无法确定一棵树的

class Solution {
private:
    // 中序区间：[inorderBegin, inorderEnd)，后序区间[postorderBegin, postorderEnd)
    TreeNode* traversal (vector& inorder, int inorderBegin, int inorderEnd, vector& postorder, int postorderBegin, int postorderEnd) {
        if (postorderBegin == postorderEnd) return NULL;

        int rootValue = postorder[postorderEnd - 1];
        TreeNode* root = new TreeNode(rootValue);

        if (postorderEnd - postorderBegin == 1) return root;

        int delimiterIndex;
        for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
            if (inorder[delimiterIndex] == rootValue) break;
        }
        // 切割中序数组
        // 左中序区间，左闭右开[leftInorderBegin, leftInorderEnd)
        int leftInorderBegin = inorderBegin;
        int leftInorderEnd = delimiterIndex;
        // 右中序区间，左闭右开[rightInorderBegin, rightInorderEnd)
        int rightInorderBegin = delimiterIndex + 1;
        int rightInorderEnd = inorderEnd;

        // 切割后序数组
        // 左后序区间，左闭右开[leftPostorderBegin, leftPostorderEnd)
        int leftPostorderBegin =  postorderBegin;
        int leftPostorderEnd = postorderBegin + delimiterIndex - inorderBegin; // 终止位置是 需要加上 中序区间的大小size
        // 右后序区间，左闭右开[rightPostorderBegin, rightPostorderEnd)
        int rightPostorderBegin = postorderBegin + (delimiterIndex - inorderBegin);
        int rightPostorderEnd = postorderEnd - 1; // 排除最后一个元素，已经作为节点了

        root->left = traversal(inorder, leftInorderBegin, leftInorderEnd,  postorder, leftPostorderBegin, leftPostorderEnd);
        root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);

        return root;
    }
public:
    TreeNode* buildTree(vector& inorder, vector& postorder) {
        if (inorder.size() == 0 || postorder.size() == 0) return NULL;
        // 左闭右开的原则
        return traversal(inorder, 0, inorder.size(), postorder, 0, postorder.size());
    }
};

leetcode 617 合并二叉树

很简单的一道题,但是我的思路没有打开,仍想着新构造一棵树而不是在原来的树上进行操作,思维上还是低级,特此记录警醒自己

 vectortmp=vector(nums.begin()+begin,nums.begin()+end);
        sort(tmp.begin(),tmp.begin());
        TreeNode*root=new TreeNode(tmp[tmp.size()-1]);
        int mid;
        for(mid=0;midval)break;
        }

在构造一个二叉树的时候我甚至想复制一个数组来获取最大值...(属于是没睡醒了),构造二叉树的题划分边界没有问题,问题出在我获取边界下标和边界的值的方式,思考问题的方法需要改变