leetcode每日一题复盘(11.6~11.12)
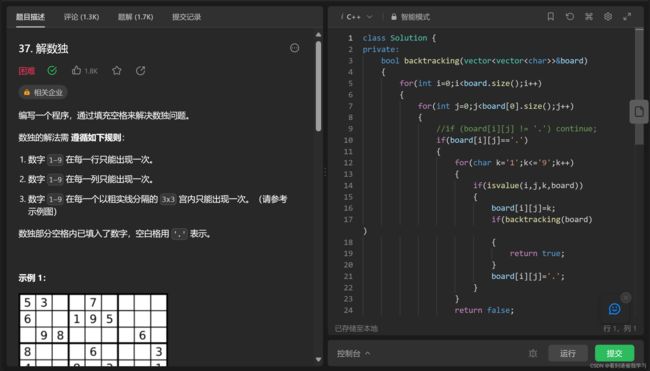
leetcode 37 解数独
回溯算法的最后一种问题:棋盘问题,前面的N皇后也是棋盘问题,只不过N皇后只需要一层放一个数据,数独需要多次放入数据且保证数据不冲突
方法是通过bool返回值进行多次递归,每次递归放入一个数据,将该层数据填满后换下一层
首先我们对比一下解数独和N皇后的区别
1.解数独每一层需要填多个数据,棋盘上每一个空格都要填满
2.解数独需要每一个小九宫格去重
因此我们需要用两次for循环,遍历棋盘的每一行每一列,再用一层for循环遍历1到9数字选择要填入的数字大小,填入的同时进行递归,将本行的全部填完;当9个数字都没有符合的时候,返回false,表示无解
其次就是如何去重的问题,除了普通的遍历行列之外,我们还要处理小九宫格里面的数据,对此我们要获取每一个小九宫格的第一个元素,通过(x/3)*3求得下标数据即可进行遍历
做这种题首先是要思路清晰,抓住每层放入的本质进行思考
leetcode 376 摆动序列
现在开始接触贪心算法了,还有十几个题型等着我呢哈哈哈,真是道阻且长啊
贪心算法就是局部求最优解,达到整体最优结果的一种算法,贪心算法并没有什么具体的模板,它更像是一种编程思想
这道题一开始是想着用双指针的办法去做的,但是代码写得不好数据一多就寄了,至于为什么会想到双指针,是因为我看到了可以删除一些元素获取子序列,也就是说数据是可以隔项的,自然仍然我就掉进了双指针的坑里,双指针不是不行,是不好写;说到底是对贪心这块知识的缺失,波峰波谷这些概念不刷题我是真不知道
所谓波峰也就是前一个差值为正,当前差值为负;波谷就是前一个差值为负,当前差值为正
那么题目就转变为求波峰波谷的数量,遇到波峰波谷子序列长度就加一
下面列举几种数据可能的情况:
1.上下坡中有平坡
2.数组两端元素
3.单调坡中有平坡
首先我们需要知道的是只要存在数据我们子序列最小长度为1,因此我们设length=1
1.上下坡中有平坡,例如12221
1到2,当前差值为正,前一个差值为0,为了兼容这种情况所以我们判断的条件前一个差值可以等于0,显然是波峰,length++
2到2,到达平坡,当前差值为0,不处理
2到1,当前差值为负,前一个差值为正(当然可以为0看你代码怎么写,为0时不符合第三种情况),为波谷,length++
2.数组两端元素,例如35
只有两个元素,我们可以在开头就进行判断大小为2排除,若不排除算前一个差值和当前差值至少需要3个元素,显然不符合
为此我们可以假设加多一个元素,335,就可以用上面那种方法去判断了,要求是允许前一个差值为0
3.单调坡中有平坡,例如123345
如果每一次遍历都更新前一个差值,这情况就会出错,在平坡的时候会把34算进去导致错误,实际上34不算是波峰,因为初始值已将最后一个元素算进去了,正确的前一个差值是12的差值1,前一个差值和当前差值都为正不能算作是摆动
1到2有一个波峰,末尾元素已算入初始值,3到4就不用算了,故答案应为2。如果实时更新前一个的差值就会出现3这样的错误答案
我们可以将其简化为15,length初始值为1,1到5,前一个差值为0,当前差值为4,length++,最终单调序列length为2
因此我们需要在摆动的时候才更新前一个差值的大小
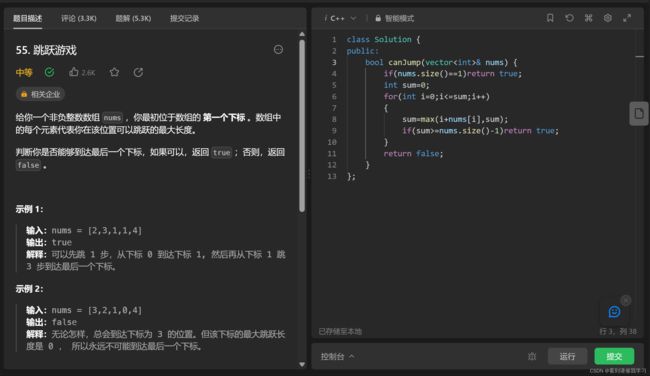
leetcode 55 跳跃游戏
最近做了几道贪心算法的题目,感觉贪心算法的特点是代码量比较少,总给人一种琢磨不透的感觉,没有什么章法可言,只能靠自己理解题目的本质,找到本质即可简化问题
跳跃问题,想倒是想的明白就是看下标和数组对应的数据之和能否大于等于最后一个下标,但是难就难在如何书写循环,因为每一次遍历会覆盖到好几个点,每一个点又覆盖其他几个点,有点类似于树的结构,写循环难以下手
理解跳跃问题的关键在于,只要能覆盖到最后一个下标就总能到达,不管以什么方式
因此我们在循环的时候选出能覆盖的点中能覆盖最远的,作为下一次的循环的主体
也就是说第一个下标对应数据为3,覆盖的数据为135,我们将选取5作为下一次循环的边界,类似与树的剪枝操作
在循环体内,找出能覆盖到的最大距离和最后一个下标进行比较,以此判断bool
leetcode 1005 k次取反后最大化数组和
一开始想到sort就以为解决了,实际上是思考深度不够,sort可以多写一个cmp函数直接比较其绝对值,这是没有想到的点,当然也可以不写,我觉得不写在做题时更容易想到
这道题的难点在于负数数量和k之间的关系处理
我们可以分成两种情况:
1.负数数量>k
这种情况在排序后直接取反即可
2.负数数量<=k
k大于等于负数的时候,所有数据都变成非负数,会出现正数取反的情况,如果k是奇数时就必须有一个数取反,为了解决这种情况我们可以再次排序,选出最小的一个正数进行取反,使得和最大化
还有一个坑就是我们在写for循环的时候可以会写遍历k次这样的循环,看似逻辑正确,但是没有考虑k与负数的关系,当k>负数数量的时候就会取反正数导致出错,所以必须记录k与负数数量的差值!
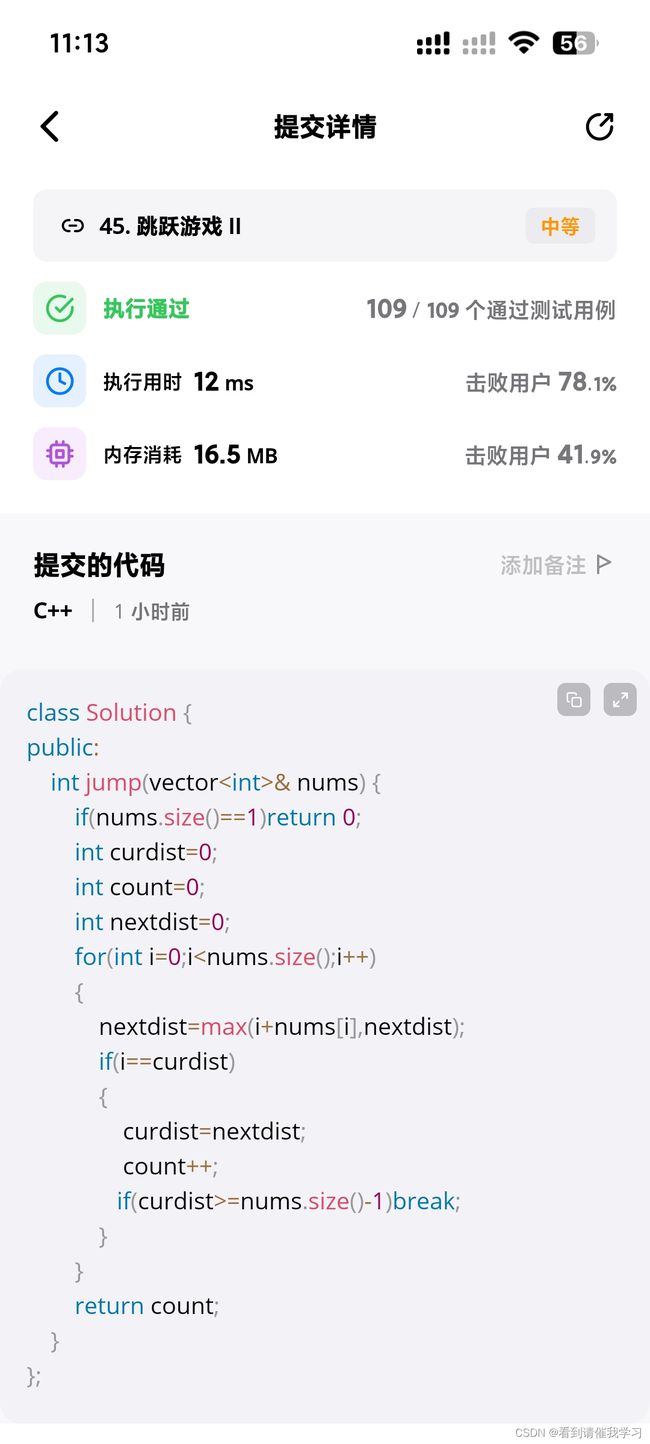
leetcode 45 跳跃游戏2
这道题和跳跃游戏稍微有些不同,我们横向对比一下:跳跃游戏是局部选优力求整体最优,判断是否能到达最后一个元素;跳跃游戏2是返回最小的跳跃次数,这就要求我们改变选择方法,每一层元素都要比较到,选出最大的元素且元素下标到达该元素时进入下一层
bool canJump(vector& nums) {
if(nums.size()==1)return true;
int sum=0;
for(int i=0;i<=sum;i++)
{
sum=max(i+nums[i],sum);
if(sum>=nums.size()-1)return true;
}
return false;
} 其实跳跃游戏的代码看起来并不是这么合理,但是可以用来判断能否到达
int jump(vector& nums) {
if(nums.size()==1)return 0;
int cur=0;
int next=0;
int count=0;
for(int i=0;i=nums.size()-1)break;
}
return count;
} 每层选出最大的,更为合理;cur是当前层能覆盖的最大距离,next是下一层能覆盖的最大距离
leetcode 134 加油站
一开始想到的是暴力循环,结果不出意料的超时了,应该是修改了测试用例,现在暴力法已经行不通了
那么贪心算法应该怎么写呢,先引用一个大佬的评论留言
假如当前一段路无法走下去了,就该放弃 换个新的起点了。这个起点最多只能到这里了,从这段路的任何地方重新开始都到达不了更远的地方了,因为放弃之前走的路都是帮你的,不然早就无法走下去了,因此 起点只能选在下一站,错的不是你,是你的起点和你的路。
贪心算法便是如此,这道题的关键点在于如何选取局部最优--当油量小于等于0时,在没油那个节点的下一个节点重新出发
为什么是在没油节点的下一个节点而不是在开始节点的下一个节点重新出发呢?
我们看一个例子,假设每一次剩下油量的序列为5,-4,1,2,3,-8在-8的时候cursum油量就小于零了,即使我们选择从-4,1……中任意一个开始都会在-8的时候停下来,因为油箱里有油(即cursum>0)才能往后走,因此-8之前的节点都不用遍历了,他们都会在-8那里停下来,我们选择在-8这个节点的下一个节点重新开始
totalsum用来计算总获得的油量和总消耗的油量的差值,小于0时永远无法到达
leetcode 135 分发糖果
一开始做感觉和摆动序列那种差不多,于是统计波峰然后发现不得行,题目还是有些许不同的,因为要求比相邻的大得到糖果就多,那么在递增的时候每次派发的糖果也是递增的
还有一个误区就是容易比较完一个节点的左边立即比较这个节点的右边,这样就没有考虑到整个序列的关系,而且派发多少数量的糖果也没有确定
所以应该先遍历比较所有的左边再遍历比较所有的右边,并且比较右边的时候需要从后往前遍历才能保证相邻孩子中评分高的拿到的糖果最多
如果不这样做,当评分高的在序列中间的时候统计的数目就会出错,第二次for循环取max是为了保证每个节点都能满足相邻之间评分高者多,这样子才能在最高点拿到最多糖果
详细解释:代码随想录 (programmercarl.com)
hard果然还是不好理解,这个还是急不来,慢慢提升能力再回来重做一次
leetcode 406 根据身高重建队列
这一题和分发糖果是同一种题目,总结一下就是题目中经常有两项数据,在分发糖果那里是左边评分差和右边评分差,在这里是身高和前面的人数,我们需要比较两个数据才能确定其位置,而同时比较一个节点的两项数据是会出错的,因为确定的位置没有考虑到其他位置的节点
因此我们必须确定下一项数据,再根据另一个数据进行调整, 也就是先根据一项数据局部选出最好的(局部取优),再根据另一项数据进行调整(整体取优)
这一题中我们选择先确定身高(因为前面的人数无法确定,有两个前面的人为0就没法排了),且确定身高高的排在前面,前面人数少的排在前面,方便后期进行调整,如果是身高矮的排前面那你插入的时候比较前面比你高的人就很麻烦了
因此排序后,再重新遍历,根据他的前面人数的个数确定下标插入到新数组中即可,因为数据都是维护好了的,所以前面的一定都是比你高的,直接插入即可