python随机生成正态分布_Python与概率统计

概率统计思维

1、随机变量

2、概率分布

3、离散概率分布

4、连续概率分布

什么是随机变量？

随机变量是指随机事件的数量表现。例如，对于随机事件“明天是否下雨”，其结果是下雨或者不下雨，我们可以将下雨定义为1，不下雨定义为0，那么这里所说的明天是否下雨的结果就是随机变量，它的取值是0和1。

什么是概率分布？

数据在统计图中的形状，叫做它的分布，概率分布就是随机事件发生的各种概率在统计图中的形状。

离散概率分布和连续概率分布

首先我们要了解一下，什么是离散型，什么是连续型。

离散型随机变量即在一定区间内变量取值为有限个或可数个，比如说抛硬币实验，它的结果只能是正面和反面，是可以计数可数的。连续型随机变量是指在一定区间内变量取值有无限个，或数值无法一一列举出来，比如明天的下雨量，它的可能结果是有无数个的，是无法枚举的。

离散概率分布和连续概率分布，就是离散型随机变量和连续型随机变量的取值概率在统计图中的形状。离散型概率分布依据概率质量函数（Probability Mass Function，PMF）分类，主要分为：伯努利分布、二项分布、几何分布和泊松分布。连续型概率分布依据的是概率密度函数（Probability Density Function，PDF），其中正态分布就是一种连续的概率分布。

下面我们通过这几种概率分布在Python上的实现来对其进行介绍。

离散概率分布

伯努利分布

伯努利实验：一个只有两种结果的实验，比如说抛硬币，它的结果只有正面和反面这两种结果，这种实验就叫伯努利实验。

在Python上绘制伯努利分布图

首先导入我们需要的数据包

定义一个随机变量，这个随机变量的取值是0和1，np.arange(0,2)这个函数也可以写成np.arange(0,2,1)，是指取0到2（不包括2）中的数字，步长是1，这个步长1可以省略，默认步长为1

使用概率质量函数PMF求出其对应的概率

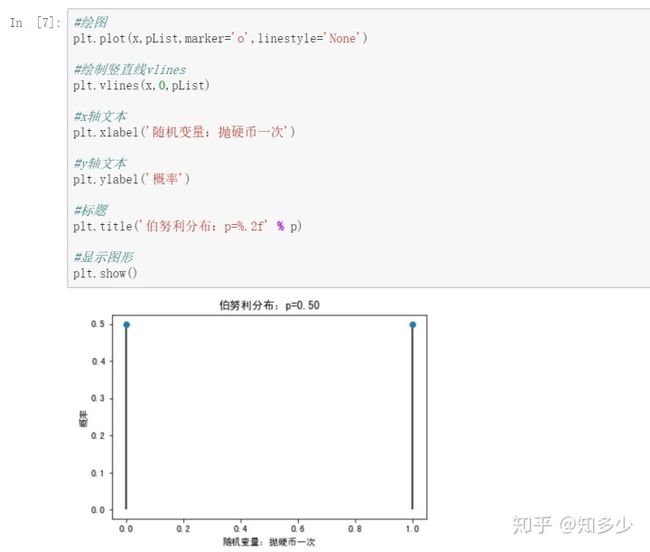
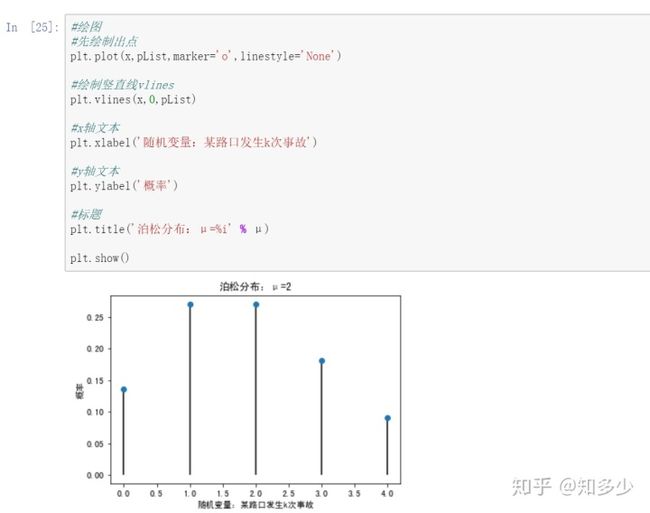
绘图

plot默认绘制折线，这里我们只绘制点，所以传入下面的参数：

marker：点的形状，值o表示点为圆圈标记（circle marker）

linestyle：线条的形状，值None表示不显示连接各个点的折线

vlines用于绘制竖直线(vertical lines),

参数说明：vline(x坐标值, y坐标最小值, y坐标值最大值)

我们传入的X是一个数组，是给数组中的每个x坐标值绘制竖直线，

竖直线y坐标最小值是0，y坐标值最大值是对应pList中的值

二项分布

二项分布即重复n次的伯努利试验，用如果事件成功的概率是P,则失败的概率q=1-p，n次独立重复试验中成功k次的概率是

P(k)= C(n,k) * p^k * (1-p)^(n-k)，其中C(n, k) =n!/(k!(n-k)!)

期望=np

方差=npq

如何检验是二项分布：

1、做某件事情的次数是固定的，次数用n表示，n次某件事是相互独立的

2、每次事件都有两个可能的结果（成功或者失败）

3、每一次成功的概率都相等，成功的概率用p表示

4、想知道成功k次的概率是多少

在Python上绘制二项分布图

定义随机变量

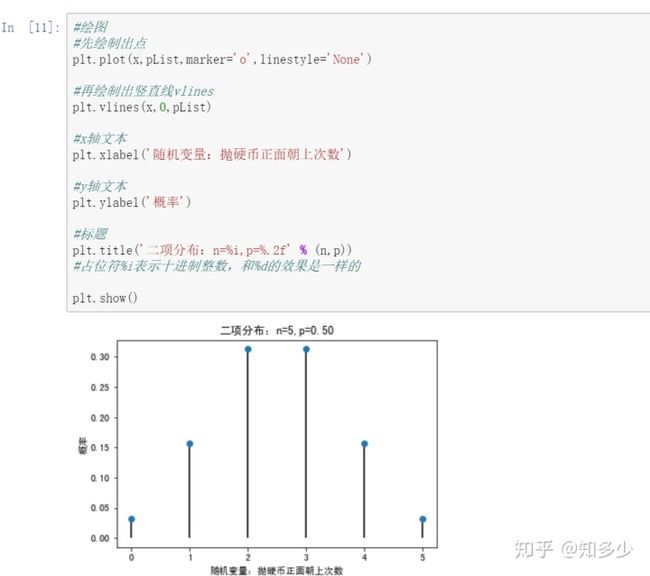
这里设定n=5，表示做5次独立随机事件，生成了0到5的一维数组，表示正面朝上的次数有可能是0到5中的任意数

运用概率质量函数PMF求出对应的概率

绘图

几何分布

几何分布是指在n次伯努利试验中，试验k次才得到第一次成功的机率。也就是说，前k-1次皆失败，第k次成功的概率。

如何检验是几何分布？

1、做某件事的次数是固定的，次数用n表示，n次某件事是相互独立的

2、每一次事件都有两个可能的结果（成功或者失败）

3、每一次成功的概率都相等，成功的概率用p表示

4、想知道第k次做某件事情，才取到第一次成功的概率是多少

在Python上绘制几何分布图

定义随机变量

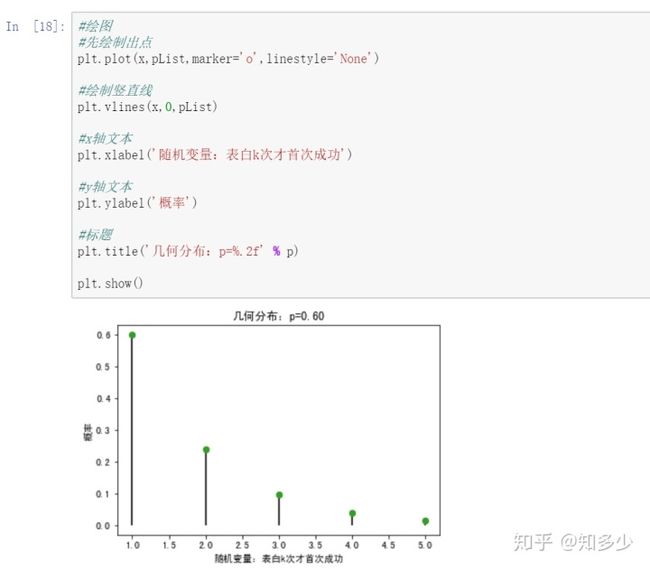
运用概率质量函数PMF求出对应的概率值

绘图

泊松分布

泊松分布适合于描述单位时间内随机事件发生的次数。实际上，泊松分布是由二项分布推导而来的，推导过程网上可以查到，感兴趣的话可以自行查看。而泊松分布与二项分布的关系是：当二项分布的n很大而p很小时，泊松分布可作为二项分布的近似，其中λ（泊松分布的期望和方差）为np。通常当n≧20,p≦0.05时，就可以用泊松公式近似得计算。

如何验证是泊松分布：

1、事件是独立事件

2、在任意相同的时间范围内，事件发生的概率相同

3、你想知道某个时间范围内，发生某件事情k次的概率是多大

在Python上绘制泊松分布图

定义随机变量：已知某路口发生事故的比率是每天2次，那么在此处一天内发生k次事故的概率是多少?

从这句话可以知道，该事件的期望和方差都是2

运用概率质量函数PMF求对应的概率值

绘图

连续概率分布

连续概率分布我们主要介绍正态分布和幂律分布两种

正态分布

用Python进行正态分布图的绘制

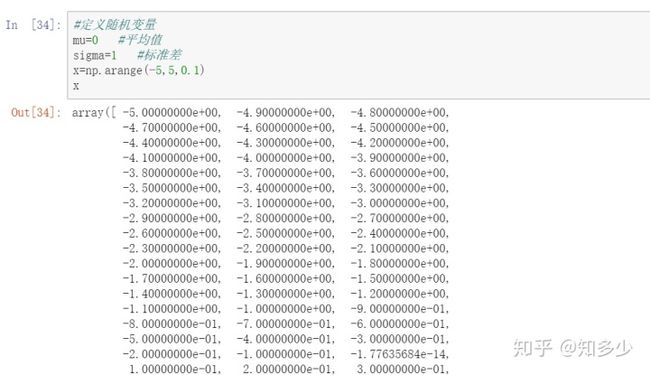
定义随机变量

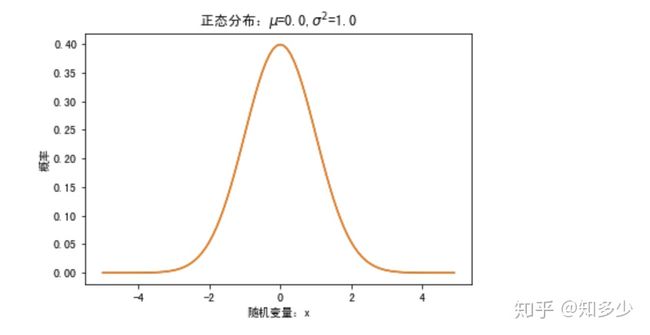
运用概率密度函数PDF求出对应的概率值，并绘制出正态分布曲线

幂律分布

幂律分布的形状，是一个不断下降的曲线，从最高的峰值开始极速下降，后面拖了一个长长的尾巴，所以幂律分布又叫长尾分布。在双对数坐标下，幂律分布表现为一条斜率为幂指数的负数的直线，这一线性关系是判断给定的实例中随机变量是否满足幂律的依据。在社会中，很多事物遵循的都是幂律分布，如财富、人口、人脉、声望等等。

总结

1、对于概率分布来说，各种概率分布虽然定义不同，表现形态不同，但其实这些概率分布之间都存在着一定的联系，基本上都可以从最开始的抛硬币事件进行推导。

2、通过Python绘制各种概率分布图可以遵循以下步骤进行：

（1）定义一个随机变量，这个随机变量的设定要符合你需要绘制的图形的相关要求

（2）根据不同的概率分布来选取不同的函数求对应的概率值，比如离散概率分布用到的是概率质量函数PMF，而连续概率分布则用的是概率密度函数PDF

（3）对于离散概率分布，我们绘制的图形要表现出是离散特点，所以建议先绘制出每个概率值对应的点，再绘制出竖直线；而对于连续概率分布，我们要表现出分布的连续性，故建议绘制出连续的曲线。