2021年中国研究生数学建模竞赛F题——航空公司机组优化排班问题
一、背景介绍
众所周知，一趟民航航班必须在满足特定的条件下才能起飞，这些条件包括国家法律法规，国际公约，政府的行政条例，和公司自身的政策利益，一些国家的工会组织还会对机组人员的福利偏好有规章约束。所有这些条件都是对保证飞航安全和旅客服务质量最重要的因素之一。
广义的机组人员包括飞行员（Pilot，或Flight Deck），乘务员（Cabin Crew）和空警（Air Marshal）。所谓机组排班问题，就是构造特定时间段的机组日程安排，包括每个机组人员在何时何地及哪个航班执行何种任务。一家100架飞机的航空公司，机组人员可以达到5000-7000之多。一个高质量的机组航班任务计划，不仅能给航空公司的运营节约成本，还能合理地考虑劳逸平衡（Work-life Balance），机组偏好（Crew Preference），组员同行（Teaming），培训（Training），时近性（Recency）和休假（Vacation Leave）等等。因为这三类机组人员不能互相通用，所以机组排班问题一般都是对他们分别求解。另外，不同机型之间的飞行员一般也不能通用，所以飞行员排班问题通常也是对不同机型分别求解。
机组排班问题是运筹学应用的最早典范之一，经过过去 ~60年的发展，虽然在计算速度和应用复杂度方面还不尽满意，但已经形成了比较成熟甚至通用的解决方案，该解决方案把机组排班问题分解成两个子问题求解：以满足规范和节约成本为主要目的任务环生成，和以满足公平合理为主要目的任务环分配，它们相对应的优化问题叫Pairing Optimization（PO）和Roster Optimization（RO）。该两问题的解决，都是通过建立网络流模型（Network Flow）然后列生成法（Column Generation）求解。列生成法易于处理各种复杂的约束条件，优化模型比较简单，在计算性能上有很大的优势，对解决分配问题非常有效，虽然算法效果的好坏也取决于子问题及算法部件的局部处理方法。
但另一方面，两阶段子问题求解法也有其明显的缺陷。比如实际排班过程中需要具备人工预排班功能，一个机组人员可能会乘坐指定航班到某地但回程却由系统安排。两阶段解法不能很好地处理这样的不完整任务环问题。而且理论上，两阶段解法缩小了优化空间，所谓的最优解其实是次优解。同时，对列生成法而言，各种规章约束参数主要是在列生成过程中考虑，优化模型本身缺乏这些约束参数的显性表达，通常的参数敏感性分析手段不能采用，因而难以对业务规则的制订起到指导作用。
本题的宗旨是建立线性优化模型，明确表达飞行时间、执勤时间、休息时间等约束，把航班直接分配给机组人员。
需要指出的是，实际应用的机组排班问题考虑因素非常繁杂。本题通过抽象合并，剔除非核心的琐碎概念和约束，但保留问题的核心复杂度。同时，学术界关于机组排班问题的各种文献只能作为对业界背景知识的了解。如果参赛者坚持参照文献中的模型及算法，敬请详列步骤。
注：Sabre公司是全球第一次采用计算机算法求解大型机组排班问题并在American Airline得以使用，也是全球第一家在任务环求解方案中对远程航段（Long Haul）引入机组增强（Augmentation）和降阶（Down Ranking）功能，并在Singapore Airline得到有效使用。中国国际航空公司（Air China）至今也一直在使用着Sabre的机组排班和管理系统Aircrews。
二、问题描述
航空公司的运营管理非常复杂，很多过程需要经过长期-中期-短期等多层次的往复循环。机组排班问题假设航班规划阶段已经完成，机型分配已经结束，对机组人员数量及资格的需求已经明确，而且可用机组人员也已经确定。机组优化排班问题的描述通过以下概念的介绍展开。
**时间：**航空公司的运营是跨时空的。本题时间的表达由年月日时分组成，秒以下的精度不计。所有时间均按单一指定时区定义（比如北京时区），相邻两天的时间分割点是给定时区的半夜零点。
**机场：**航班的起飞和到达，及机组人员的出发和到达，都是以机场为节点。机场的标识一般按照国际民航组织IATA标准。比如北京首都机场PEK，上海浦东国际机场PVG。
**机组人员（Crew）：**本题的描述只针对飞行员，但对乘务员和乘警完全适用。现代民航飞机的驾驶通常需要两种资格的飞行员：正机长（也叫机长或正驾驶，Captain）和副机长（也叫副驾驶，First Officer）。
- 每个机组人员都有一个固定的基地，用所在地机场表达。
- 每个机组人员都具有一个且仅有一个主要资格，但也可以具备其它的替补资格。机组排班优先安排主要资格，但当主要资格不足时，可以安排替补资格。本题假定具备正机长资格的飞行员其主要资格是正机长，否则其主要资格是副机长。部分正机长可以替补副机长执行飞行任务。机组人员按主要资格或替补资格执行的任务都叫飞行任务。
- 机组人员除了执行飞行任务外，还可以执行乘机（Deadhead）任务。乘机任务是指机组人员乘坐正常航班从一机场摆渡到另一机场去执行飞行任务。注：乘机人数一般会有限制。
**航班（Flight）：**指飞机的一次起飞和降落。本题假定每个航班都是唯一的，虽然实际情况下的航班号可能按天或星期重复。注：当航班应用于机组人员排班时也叫航段（英文Leg或Sector）。
- 每个航班都有给定的起飞日期、时间，和到达日期、时间。
- 每个航班都有给定的起飞和到达机场。
- 每个航班都有给定的最低机组资格配置（Composition），用格式C<数> F<数> 描述，其中C<数>为正机长数，F<数>为副机长数。一个航班只有满足了最低机组资格配置才能起飞。注：本题假定只有一种机型一种配置，实际情况可以有所不同。
**执勤（Duty）：**一次执勤由一连串航段（飞行或乘机）和间隔连接时间组成，相当于一次上班。同一次执勤的航段之间满足如下关系：
- 上一趟航段的到达和下一趟航段的出发机场一致。
- 上一趟航段的到达和下一趟航段的出发之间的间隔时间必须满足最短连接时间约束。
- 同一次执勤里的每个航段必须在同一天起飞，但到达时间不受此限制。按起飞时间，我们说这次执勤属于那一天。
航段之间的连接时间计入执勤时间，但不计入飞行时间。执勤起始时间从当天所执行的第一趟航班的起飞时间算起，结束时间按最后一趟航班的到达时间计算。因此，执勤结束时间可以不和该执勤开始时间在同一天。
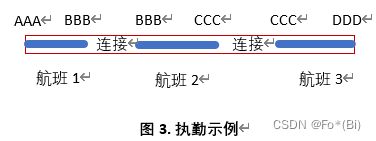**任务环（Pairing）：**任务环由一连串的执勤和休息时间组成，从自己的基地出发并最终回到自己的基地，相当于一次出差。属于同一任务环的执勤之间满足如下关系：
- 上一次执勤的结束机场必须和下一次执勤的起始机场相一致；
- 两个相邻执勤之间的休息时间必须满足最少休息时间限制，但没有上限；
- 每个任务环里的第一次执勤必须从基地出发，最后一次执勤必须回到基地。
**排班计划（Roster）及排班周期：**每个机组人员在每个排班周期都有一个排班计划，这个计划由一系列的任务环和休假组成，任务环之间满足一定的休假天数。一个排班周期通常是两个星期（双周计划）或者一个月（月计划）。机组人员的排班计划按排班周期编排，每个周期开始前几天完成编排并向机组人员发布。
排班周期之间有严格的时间分割，机组人员在给定排班周期内的最后一个任务环可能跨越这个时间分割点而进入下一个排班周期。为减少模型复杂度，本赛题假定所有机组人员的初始位置和排班周期结束时的终了位置都是在其基地，并把排班周期进行了适当的延展。
三、赛题
本赛题由三个子问题组成，每个子问题都基于前一个子问题并与之相容。如果概念定义和过程描述与业界有所出入，皆以本赛题为准。凡是本赛题没有提及，均不在考虑之列。本题假定：
- 机组人员之间可以任意组合；
- 允许存在因为无法满足最低机组资格配置而不能起飞的航班；
- 不满足最低机组资格配置的航班不能配置任何机组人员；
- 机组人员可以乘机摆渡，即实际机组配置可以超过最低配置要求，乘机机组人员的航段时间计入执勤时间，但不计入飞行时间。
**子问题1：**基本题。要求建立线性规划模型给航班分配机组人员（或者说给机组人员分配航班），依编号次序满足目标
①. 尽可能多的航班满足机组配置;
④. 尽可能少的总体乘机次数；
⑦. 尽可能少使用替补资格。
约束：
- 每个机组人员初始从基地出发并最终回到基地；
- 每个机组人员的下一航段的起飞机场必须和上一航段的到达机场一致；
- 每个机组人员相邻两个航段之间的连接时间不小于 MinCT分钟。
本子题要求编程，并按所给数据运行，输出结果要求见第五部分。
**子问题2：**引进执勤概念。假定每个机组人员 的每单位小时执勤成本给定（可以设想为小时工资）。本子问题除了需要满足子问题1的所有目标外，还需满足如下目标（依编号次序）
②. 机组人员的总体执勤成本最低；
⑤. 机组人员之间的执勤时长尽可能平衡。
同时在满足子问题1约束的基础上进一步要求：
- 每个机组人员每天至多只能执行一个执勤；
- 每次执勤的飞行时间最多不超过MaxBlk分钟；
- 每次执勤的时长最多不超过 MaxDP分钟；
- 每个机组人员下一执勤的起始机场必须和上一执勤的结束机场一致；
- 每个机组人员的相邻两个执勤之间的休息时间不小于 MinRest分钟。
本子题要求编程，并按所给数据运行，输出结果要求见第五部分。
子问题3： 编制排班计划。假定每个机组人员 的每单位小时任务环成本给定（注：不包括执勤成本，可以设想为出差补贴）。本子问题除了需要满足子问题1和2的所有目标外，还需满足如下目标（依编号次序）
③. 机组人员的总体任务环成本最低；
⑥. 机组人员之间的任务环时长尽可能平衡。
同时在满足子问题1和2的约束的基础上进一步要求：
- 每个机组人员每个排班周期的任务环总时长不超过 MaxTAFB 分钟；
- 每个机组人员相邻两个任务环之间至少有MinVacDay天休息。
- 每个机组人员连续执勤天数不超过MaxSuccOn天
本子题要求编程，并按所给数据运行，输出结果要求见第五部分。
四、输入数据说明
本题有两套检测数据，要求参赛者优先运行A套数据，然后再B套数据。
每套输入数据由三部分组成，除输入参数在这里给出外，航班计划和机组人员数据需要另外下载，这里仅给出格式描述。
1、输入参数：
• 航段之间最小连接时间 MinCT = 40分钟
• 一次执勤飞行时长最多不超过 MaxBlk = 600分钟
• 执勤时长最多不超过 MaxDP = 720分钟
• 相邻执勤之间的休息时间不少于 MinRest = 660分钟
• 每趟航班最多乘机人数 MaxDH = 5
• 排班周期单个机组人员任务环总时长不超过 MaxTAFB = 14400分钟
• 连续执勤天数不超过MaxSuccOn = 4天
• 相邻两个任务环之间至少有MinVacDay =2天休息
2、 航班计划数据格式
3、机组人员信息数据格式：
五、提交结果要求
参赛选手必须按比赛规则提交规定格式的论文报告。此外，本赛题还有如下要求：
1、建立完整的数学模型
- 模型所用变量和参数都需要解释清楚。变量一般用单个小写英文字母表示；参数可以是希腊字母，也可以是第一个字母大写的英文字符串，但需要尽可能简洁；下标尽可能只用单个小写的英文字母表示。为简洁易读易懂起见，变量可以有上撇（’），上横（ ̅ ）等辅助记号；
- 所有变量、参数和记号都必须通篇前后一致。
2、根据模型设计求解算法
- a. 模型和算法是两个独立的概念。提交的论文必须对数学模型的特点进行分析，包括模型的规模和结构，求解的难易，等等；
- b. 算法必须针对数学模型的特点设计。论文需要解释算法的合理性，包括算法实现的难易，复杂度估计和运行时间分析。如果采用实用性算法，必须解释算法的思路；
- c. 模型算法描述必须逻辑严谨，条理清晰，同时简单易懂。
3、编写程序算法，并使用给定数据进行实验
- a. 程序编写可以按自己的专长选用高级语言或脚本语言，或多种方法的组合，求解器可以是商用、开源、自主开发，由参赛者根据自己的情况选择。
- b. 程序必须模块化，结构要面向目标，注释清晰；
- c. 参赛选手需要在报告附录中介绍程序和数据结构。
4、论文报告必须明确包括如下数据，同时欢迎作者采用其它图表形式对实验结果进行描述，但要求设计简单易懂，线条清晰，色彩分明，重点突出，标注恰到好处。
5、本赛题还需提交程序实现的计算结果，及如下两个文本文件：
- a. 按拟起飞日期和时间，出发和到达机场的次序，罗列没有机组配置的航班号和其最低配置需求。此结果需从Excel 表格按CSV
格式导出，数据项名称简单易懂，用文件名 “UncoveredFlights.csv” 提交。 - b. 按机组人员，按日期，按航段次序，罗列该机组人员的航班分配，需注明航班号，起飞日期时间/机场和到达日期时间/机场，任务性质（机长，副机长，替补，乘机）等。如休假日也需注明。此结果需从Excel
表格按CSV 格式导出，数据项名称简单易懂，用文件名 “CrewRosters.csv” 提交。
参考文献
- Xiaodong Luo, Yogesh Dashora, Tina Shaw (2015) Airline Crew Augmentation: Decades of Improvements from Sabre. Interfaces 45(5): 409-424.
- Saeed Saemi, Alireza Rashidi Komijan, Reza Tavakkoli-Moghaddam and Mohammad Fallah, A new mathematical model to cover crew pairing and rostering problems simultaneously, Journal of Engg. Research Vol. 9 No. (2) June 2021 pp. 218-233
- Mohamed Haouari, Farah Zeghal Mansour, Hanif D. Sherali (2019) A New Compact Frmulation Fr the Daily Crew Pairing Problem. Transportation Science 53(3): 811-828