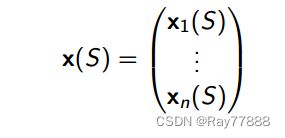强化学习6:值函数近似 Value Function Approximation
我们学习了在Model Free环境下分别使用MC, TD进行策略评估的策略控制方法。并按照学习方式划分为On Policy和Off Policy两种类型,比如Sarsa和Q-Learning两类表格型方法。
表格型方法在大规模强化学习环境中表现不好,因为需要保存所有的状态动作对的价值所以会耗费很大的时间与空间。因此我们可以采用函数近似代替表格型方法,也就是用一个函数来表示价值,然后训练这个函数,当我们输入状态S时,让它可以近似的输出价值V。同时采用MC或TD方法更新近似参数 w。近似函数需要满足可导条件,我们常使用线性函数或者神经网络进行函数近似。
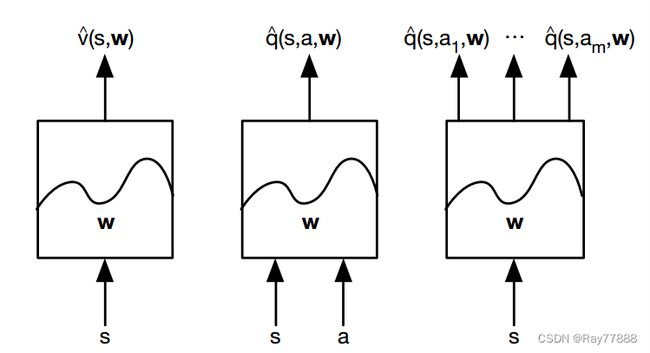
- 第一种,针对状态本身,输入S,输出状态的近似状态价值函数
- 第二种,针对状态行为对,输入S,a对,输出s状态下动作a的Q值的近似。
- 第三种也是求Q的近似,但是改变了模型的结构,针对状态本身,只输入s,输出各个动作对应的Q值的近似。
额外补充:
当我们做免模型控制的时候,我们主要估计Q值,所以这里我主要看下后面两种方式,哪一种好呢?我们说一般是第二种好, 因为当我们需要近似的时候,说明状态的个数比较庞大,而一般我们的智能体的动作不会很大,比如Atari游戏,状态数以百万,每一个像素的 变化都是一个新的状态,但是动作可能只有几个,向左,向右,攻击之类的。所以造成了两个输入的维度相差太大,不利于训练。 其实还有一个好处,就是第二种模型,你需要每个状态动作对都输入一次,因此你计算了很多次网络的向前传播,而第三种方式只需要输入一次。
常见的Funcion Approximator的手段:
Linear combinations of features
Neural network
Decision tree
Nearest neighbor
Fourrier(傅里叶变换) / wavelet basses
在本讲中,主要考虑前两类,即用可导函数来做Approximation
Incremental Methods 增量方法:
梯度的定义:(J是一个从空间V到 R \mathbb{R} R的函数)。

梯度下降(批梯度下降,Batch Gradient Descent):
假设已知真实的价值函数,我们希望最小化真实的价值函数 v π ( s ) v_\pi(s) vπ(s)与近似函数的均方误差的期望,从而实现对价值函数的近似。
随机梯度下降(Stochastic Gradient Descent):
特征向量(Feature Vector):
用一个特征向量表示一个状态,每一个状态是由以w表示的不同强度的特征来线性组合得到:
参数更新量 = 步长( α \alpha α) × 预测误差 × 特征值
step size * prediction value * feature value
Table Lookup Features
查表(Table Lookup)也是一种特殊的线性函数近似,每一个状态对应一个参数(该状态的估计价值。)
增量预测算法
Monte-Carlo with Value Function Approximation,TD Learning with Value Function Approximation, TD(λ) with Value Function Approximation,思想都是一样的,区别只是target的形式不一样。
所以我们一般用target带代替值函数,什么target呢?MC中就是未来折扣回报Gt,TD(0)里就是TD target : R t + 1 + γ v ( S t + 1 ; w ) Rt+1 + γv ^(St+1; w) Rt+1+γv(St+1;w), TD(λ)里就是λ-return Gtλ。
值函数近似控制
前面讲的都是值函数的估计,也就是Predcition预测的部分,现在开始讲控制的部分。自然,如果还记得上一篇笔记中的内容的话, 我们现在就不应该估计状态价值函数了,而是应该估计动作价值函数Q,这样才能真正的免模型。增量控制算法和增量预测算法思想是一样的,只是V都换成了Q。也没什么特别注意的地方。
收敛性
首先是预测算法的收敛性,在On-policy与Off-policy下都是MC最优。从预测算法的收敛性上可以看到TD算法的Off-policy上的收敛性较差,但是如果使用Gradient TD会好很多。
批量方法(Batch Method)
上面讲到现在都还是增量方法,但是其采样效率很低,现在开始讲批量方法,批量方法进行批量得对训练数据进行学习,优势就是sample efective,可以更大程度的利用训练数据,具有更高的效率。批量方法的这些优势正是增量方法没有的。
批量方法要在最大化利用数据的同时去找到对于值函数最好的拟合。
使用经验回放(Experience Replay)的SGD
在给定经验池时,我们可以重复下面两个步骤应用SGD:
- 从经验池 D D D中进行(state,value)对的采样: ⟨ s , v π ⟩ ∼ D \left\langle s, v^{\pi}\right\rangle \sim \mathcal{D} ⟨s,vπ⟩∼D
- 应用SGD进行参数更新: Δ w = α ( v π − v ^ ( s , w ) ) ∇ w v ^ ( s , w ) \Delta \mathbf{w}=\alpha\left(v^{\pi}-\hat{v}(s, \mathbf{w})\right) \nabla_{\mathbf{w}} \hat{v}(s, \mathbf{w}) Δw=α(vπ−v^(s,w))∇wv^(s,w)
这样的结果可以收敛到最小二乘解: w π = argmin w L S ( w ) \mathbf{w}^{\pi}=\underset{\mathbf{w}}{\operatorname{argmin}} L S(\mathbf{w}) wπ=wargminLS(w)
最小二乘法预测
DQN算法的成功就是主要使用了经验池与固定的目标Q网络两种技术,其关键在于以下几点:
-
使用 ϵ − g r e e d y \epsilon-greedy ϵ−greedy策略选取动作 a t a_t at
-
将产生的转移数据 ( s t , a t , r t + 1 , s t + 1 ) \left(s_{t}, a_{t}, r_{t+1}, s_{t+1}\right) (st,at,rt+1,st+1)存储到经验池 D D D中
-
从经验池 D D D中随机采样一个小批量的经验数据 ( s t , a t , r t + 1 , s t + 1 ) \left(s_{t}, a_{t}, r_{t+1}, s_{t+1}\right) (st,at,rt+1,st+1)
-
根据旧的,并且固定的参数 w − w^- w−计算Q函数的目标值
-
优化Q-network和Q函数目标值之间的目标函数MSE: L i ( w i ) = E s , a , r , s ′ ∼ D i [ ( r + γ max a ′ Q ( s ′ , a ′ ; w i − ) − Q ( s , a ; w i ) ) 2 ] \mathcal{L}{i}\left(w{i}\right)=\mathbb{E}{s, a, r, s^{\prime} \sim \mathcal{D}{i}}\left[\left(r+\gamma \max {a^{\prime}} Q\left(s^{\prime}, a^{\prime} ; w{i}^{-}\right)-Q\left(s, a ; w_{i}\right)\right)^{2}\right] Li(wi)=Es,a,r,s′∼Di[(r+γmaxa′Q(s′,a′;wi−)−Q(s,a;wi))2]
使用SGD进行参数更新