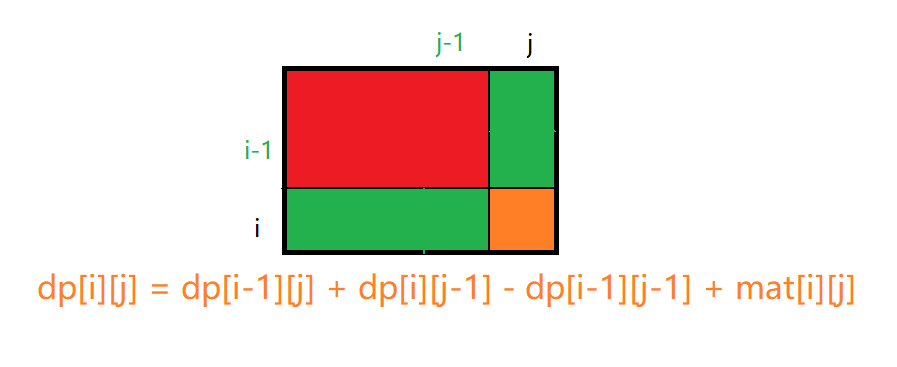前缀和——1314. 矩阵区域和

1. 题目

题目链接：1314. 矩阵区域和 - 力扣（LeetCode）

给你一个 m x n 的矩阵 mat 和一个整数 k ，请你返回一个矩阵 answer ，其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和：

• i - k <= r <= i + k,
• j - k <= c <= j + k 且
• (r, c) 在矩阵内。

示例 1：

输入：mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出：[[12,21,16],[27,45,33],[24,39,28]]

示例 2：

输入：mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2
输出：[[45,45,45],[45,45,45],[45,45,45]]

提示：

• m == mat.length
• n == mat[i].length
• 1 <= m, n, k <= 100
• 1 <= mat[i][j] <= 100

2. 算法原理

这题的意思就是给我们一个mat矩阵，然后我们返回一个ans矩阵，ans矩阵和mat同等规模，以当前位置为圆心，k为半径，辐射所有元素的和，如下图示例：

这里其实就是一个求二维前缀和的操作，不了解的可以看一下此篇文章：前缀和——DP35 【模板】二维前缀和

初始化前缀和矩阵：

不需要硬记模板，要用的时候，画一个草图，直接推一下就好了

dp[i][i] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + mat[i][j]

使用前缀和矩阵：

我们要求的最终结果也是，画一个草图，直接推出来

ans = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]

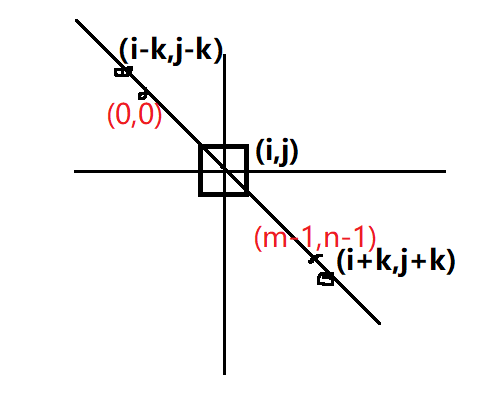
当我们要ans[i][j]这个位置的值的时候，需要找到对应的矩阵。

由于是向四周延申，我们只需要左上角和右下角的坐标即可，即(i-k，(j-k)和(i+k)，(j+k)

边界处理：在找左上角和右下角坐标的时候，可能会发生越界，这里我们需要处理一下。

假设左上角坐标为(x1,y1)，那么x1 = max(0,i-k)，y1 = max(0,j-k)

右下角坐标为(x2,y2)，那么x2 = min(m-1,i+k)，y2 = min(n-1,j+k)

下标映射关系：

我们上面这个DP【35】二位前缀和模板这题，下标其实是从(1,1)开始的，而本题是从(0,0)开始的。

所以我们填dp表的时候可以多加一行一列，便于我们处理

那么这里的dp公式需要稍微修改一下：dp[i][i] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + mat[i-1][j-1]；

要填ans去使用这个dp表的时候，下标统一+1，我们可以直接在求下标的时候+1。

即x1 = max(0,i-k)+1，y1 = max(0,j-k)+1，x2 = min(m-1,i+k)+1，y2 = min(n-1,j+k)+1

3. 代码实现

class Solution {
public:
    vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
        int m = mat.size(),n = mat[0].size();

        vector<vector<int>> dp(m+1,vector<int>(n+1));
        for(int i=1;i<=m;i++)
        {
            for(int j=1;j<=n;j++)
                dp[i][j] = dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+mat[i-1][j-1];
        }
        vector<vector<int>> ans(m,vector<int>(n));
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                int x1 = max(0,i-k)+1, y1=max(0,j-k)+1;
                int x2 = min(m-1,i+k)+1, y2=min(n-1,j+k)+1;
                ans[i][j]=dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1];
            }
        }
        return ans;
    }
};

运行结果：