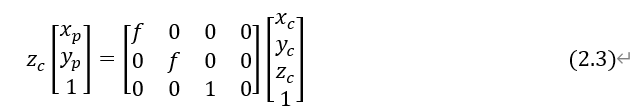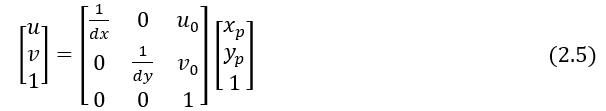基于二维标定物的相机标定---张正友相机标定法

毕业设计做了相机标定相关的工作，想着把理论和实现方法总结一下发出来，算是个记录，如果能帮助到有需要的人就更好了。

提前说明，这篇文章主要是将我的本科毕业论文中的相关部分进行提取、修改的结果，文中公式采用截图的方式给出（不知道怎么用公式编辑器…)，所以对应的公式号与章节号可能不符，读者请注意。

摘要

本文使用的方法是张正友的相机标定法

Z. Zhang, “A flexible new technique for camera calibration,” in IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 22, no. 11, pp. 1330-1334, Nov. 2000.

相机标定是整个标定过程的前提，其目的是为了得到相机的内参数和外参数，内参数包括相机的焦距、镜头畸变参数、主点等信息，外参数包括像素坐标系相对于世界坐标系的旋转、平移矩阵。通过相机标定，我们可以知道像素坐标系与世界坐标系直接的转换关系，也就是要求的单应性矩阵，通过相机标定我们可以知道的是，在图像上看到的物体在实际中相对相机坐标系的位姿。

1、相机标定各坐标系的介绍

相机标定中共4个坐标系：世界坐标系(x_w,y_w,z_w)、相机坐标系(x_c,y_c,z_c)、图像坐标系（x,y）、像素坐标系(u,v)。
各坐标系对应位置关系如图1所示。

世界坐标系(x_w,y_w,z_w)：在真实世界中的坐标系，相机标定中所选用的世界坐标系通常是以标定板所在平面为坐标系的XoY面。
相机坐标系(x_c,y_c,z_c)：相机所在的坐标系，用于描述相机的位姿状态，在相机标定中通常用于连接世界坐标系与图像坐标系。
图像坐标系（x_p,y_p）：即相机传感器所在的坐标系，用于描述物体在成像过程中的投射关系，在相机标定中用于连接相机坐标系与像素坐标系。
像素坐标系(u,v)：是我们在屏幕上所看到的图片所在的坐标系，在相机标定中用于直观的展示物体的位姿信息。

2、各坐标系之间的齐次坐标转换

本文采用张正友相机标定法[2]，该方法将上文介绍的不同坐标系之间的关系转换为矩阵相乘的形式，最终得到世界坐标系与像素坐标系之间的对应关系，即单应性矩阵。坐标系之间的转换分为以下几个步骤，分别是：（1）世界坐标系与相机坐标系之间的转换;(2) 相机坐标系与图像坐标系之间的转换;(3) 图像坐标系与像素坐标系之间的转换；（4）内参矩阵的求解；（5）单应性矩阵的求解，将上述几个个转换关系和计算过程进行结合就得到像素坐标系与世界坐标系之间的转换关系，也就是说可以从相机捕捉到的图片中推导出物体在三维世界中的位置信息。下面将一一介绍这几个关系转换的推导步骤。

2.1、世界坐标系与相机坐标系之间的转换

在相机标定中，通常使用旋转矩阵和平移向量来表示物体在世界坐标系下与相机坐标系的相对位姿关系，即：

在上述公式中，为了计算方便，假设标定板所在平面为世界坐标系的XOY平面，即世界坐标系的Z=0。而变换矩阵[R33 T31]（第二条等式左边的矩阵）就是外参矩阵。

2.2、相机坐标系与图像坐标系之间的转换

该变换过程将被摄物体从三维坐标转换至二维坐标，所用到的原理是投影透视原理。

假设相机坐标系中有一点C(x_c,y_c,z_c)，则在理想图像坐标系下（无畸变）的成像点P（x_p,y_p）的坐标为:

将上式转换为矩阵形式，得：

其中f为相机的焦距。

2.3、图像坐标系与像素坐标系之间的转换

由于像素坐标系原点与图像坐标系原点不重合，假设图像坐标系原点在像素坐标系下的坐标为 (u_0,v_0)，每个像素点在图像坐标系x轴、y轴方向的尺寸为：dx、dy，且像点在图像坐标系下的坐标为(x_p,y_p)，于是可得到像点在像素坐标系下的坐标为：

转换为矩阵形式：

2.4、内参矩阵的求解

将3式与5式相乘，得到内参矩阵：

其中，

综上所述，可得像素坐标系与世界坐标系的转换关系，即：

其中
(u,v)为像素坐标，可从图片中获取；
(x_w,y_w)为世界坐标系下的坐标，在相机标定中即为标定棋盘角点的坐标；
s为尺度因子，无实际意义，仅用于方便计算，u_0、v_0、r_1、r_2、t、γ为待求量。

2.5、单应性矩阵的求解

单应性矩阵用于描述物体在世界坐标系下的位姿与像素坐标系的位姿的相对关系，通过上述的推导，可以将单应性矩阵表示如下：

则式(2.7)可表示为：

令

其中h_33为齐次坐标，值为1。则在H矩阵中有8个未知量，对于世界坐标系和像素坐标系中的一对点(x_w,y_w) 和(u,v)，由可知式（2.9）存在两个方程，则至少需要4对点就可以求出H矩阵中的全部值。

3、相机内外参数求解

在上文中已经求解出H矩阵，接下来就要分别求解内参矩阵和外参矩阵。在张正友相机标定中使用的方法为先求解内参矩阵，再代入H矩阵求解外参矩阵。具体方法如下。

3.1、求解内参矩阵

首先令

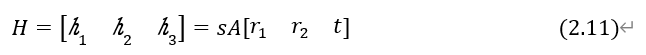
则可得关于h的方程组：

方程组（2.12）可转换为关于r的方程组：

关于上式可得出两个约束条件：
r_1与r_2正交。
r_1与r_2的模相等。
即：

令

从矩阵中可以看出，B为对称矩阵，因此共有6个未知数。令这六个未知数构成向量b：

对式(2.14)做进一步化简：

其中

于是，可将两个约束条件表示为矩阵的形式：

对于式(2.20)中系数矩阵中的值已在求单应性矩阵时得到，所以仅需求b中六个未知数。

对于一张图片可得一组式（2.20）表示的矩阵，若要求b中6个参数，则至少需要3张图片。

在求解出b向量后将数据带入B矩阵，再用cholesky分解得内参矩阵A。

3.2、基于内参矩阵求解外参矩阵

由式(2.12)可得外参矩阵各参数的求解公式：

其中

至此，已经完成了相机标定的初始参数求解部分。

4、基于极大似然估计求解畸变参数

4.1、极大似然估计

在上述部分已经求得了相机的初始参数，接下来将求得的参数带入似然函数对所求得的参数进行优化，使得参数更接近真实值，似然函数如下：

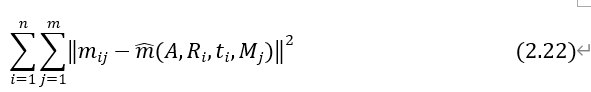
再结合L-M算法即可求得最优参数。

4.2、径向畸变处理

相机的畸变主要包括径向畸变与切向畸变，在张正友相机标定法中仅考虑径向畸变，因此在本文中也只进行径向畸变处理。
假设(u,v)为理想像素坐标系下的坐标，(u ̅,v ̅)为实际像素坐标系下的坐标，(x,y)为理想图像坐标系下的坐标，(x ̅,y ̅)为实际图像坐标系下的坐标。k_1、k_2为径向畸变系数。于是有：

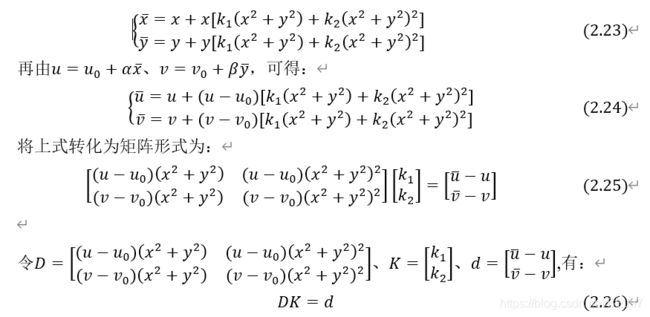
在上式中，理想坐标系的坐标由推导得来，世界坐标系的坐标通过读取相机、图片的数据得来，均为已知量，未知量为k_1、k_2。

在图像坐标系和像素坐标系上的每一对点都可得上述的一组矩阵。已知n副图的m个点，则有2nm个等式。利用最小二乘法可求得K矩阵中的值，即：

再将求得的畸变系数k_1、k_2进行极大似然估计，得到最优参数，公式如下：

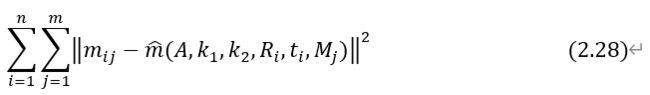
同上文一样，再次使用L-M算法进行求解，最终可得相机标定的最优参数。

5、代码实现及文件共享

至此，就是张正友相机标定法的理论部分的全部内容了，关于代码实现的部分，读者可以参考下面的链接。

测试代码所需的图片我上传到了百度云，各位没有积分的可以去这里下载，提取码为pr1y
为了防止百度云链接失效，再上传一份至CSDN