TsunderexD

2023-10-18-雷达DoA算法-MUSIC算法

Written by author：由于作者还是学生，研究的方向是毫米波雷达，因此作者希望通过每天写一篇博客的形式来记录并巩固自己每天所学习的知识，同时也锻炼自己的总结能力，故文中可能会出现一些理论上的错误或者引用错误，恳请读者指正！！

1、前言

之前的三篇文章已经简要介绍了毫米波雷达的一些基本的原理，之后便会对一个基础的较为系统的雷达系统进行逐步的分析（主要是作者看到哪个方法便会记录哪个方法、后续方法多了的话会进行一个整理）。

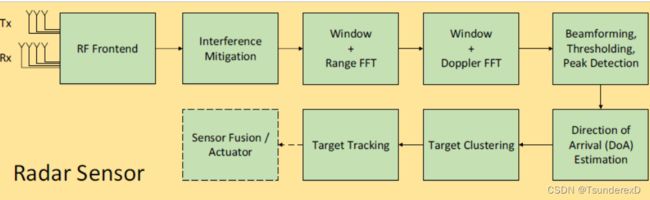
作者最近在看毫米波雷达的一些应用，发现毫米波雷达可以用于很多场景，例如生理参数的检测、物体的定位、手势的识别等等...下图便是一个较为典型的基础的车载毫米波雷达信号处理的流程。

该图较为清晰的展现了一个车载毫米波雷达系统的流程。从雷达射频前端采集到的模拟信号，通过高速ADC转换成为数字信号，将数字信号送入单片机内进行进一步的信号处理。内部的处理单元首先会对该时域信号进行一些干扰以及杂波的抑制，之后分别进行range-FFT和doppler-FFT的信号处理，得到多个天线的二维range-doppler频域结果图。在此基础上进一步处理，比如数字波束成形（DBF），通过恒虚警率（CFAR）过滤，筛选出点目标等等。之后对已经过滤出的点目标进行角度计算，接着基于提取出的点目标距离、速度和角度信息，将它们聚类，因为实际上来自同一个较大反射面积的目标可能会有多个反射点，聚类算法就是找出可能来自同一个目标的点集。上述一系列步骤完成了目标检测，之后就是目标跟踪，由于实际物体目标的距离、速度和角度不可能在较短时间内（雷达信号处理周期一般是50ms-70ms）变化较大，利用这个性质对目标的运动轨迹进行跟踪预测，结合本车的运动信息，来判断目标是否有可能出现在汽车的运行轨迹上。

上述出现了很多作者之前从未听说过的一些信号处理方法。例如DBF、CFAR、Clustering、DoA等这些英文词汇。因此作者最近的目标就是对这些概念以及其内容进行一个较为详细的解释。

本文会首先详细讲述DoA中的其中一个算法MUSIC算法的原理和应用。

2、简介

在学习MUSIC算法之前，我们需要了解一些基础的知识。

2.1、DBF（波束形成）

波束形成技术通过调节各天线的相位使信号进行有效叠加，产生更强的信号增益来克服路损，从而为无线信号的传输质量提供了强有力的保障。

波束形成算法的关键是寻找最佳权矢量，使得接收到的信号通过W加权后，期望信号加强，其它干扰信号则被抑制。

波束形成也叫空域滤波。

按照是否考虑幅度加权，波束形成分为两大类：相位加权、幅相加权。幅相加权是要进行零陷考虑，各种dbf准则就是针对幅相加权。现在研究都集中在幅相加权上，对于单纯相位加权，没什么可研究的。因此常说的波束形成算法一般都指幅相加权。

用大白话说，DBF就是提高所需信号方位的信号强度，抑制其他方向的信号，从而达到增强所需信号的效果。

2.2、DoA（Direction of arrival）

时域频谱表示信号在各个频率上的能量分布；空间谱表示信号在空间各个方向上的能量分布。所以如果能够得到信号的空间谱，就能够得到信号的波达方向 (Direction of arrival, DOA) 所以空间谱估计也被称为DoA估计。

DoA的基本原理是：测量相位差，根据阵列结构，就能知道信号来向。

DoA是阵列信号处理的两个主要方向之一，阵列信号处理的另一个方向是DBF。二者相辅相成，很多地方是共通的，实质上是一个整体。

用大白话说，DoA就是通过测量信源发送到接受天线的电磁波，从而确定信源相对于接受天线的方向。

2.3、常见的DoA算法

雷达到达角估计是雷达信号处理中的一个重要问题，旨在确定来自目标的雷达信号的到达角度。下面是一些常用的DoA算法。

1、CBF算法

传统时域傅里叶谱估计方法在空域中简单拓展形式，空间分辨能力会受到“瑞利限”的限制

2、3D-FFT算法

通过对雷达接收信号进行傅里叶变换，将空域信息转换到频域的方法。在频域中，可以通过对接收信号的各个方向进行傅里叶变换，得到不同方向的空间频率响应，从而推导出目标的到达角。估计精度受到阵列的几何结构、信噪比和多径等因素的影响，无法有效地估计高动态范围和高速移动目标的到达角。

3、CAPON算法

又叫最大方差无畸变算法，通过对与信号协方差矩阵以及阵列方向矢量相关的空间谱函数进行二维谱峰搜索,得到信源方向角的估计结果。可以克服瑞丽限。

4、MUSIC算法

子空间算法，利用导向矢量与噪声子空间的正交性。可以克服瑞丽限。

5、ESPRIT算法

子空间算法，利用子阵间信号子空间的旋转不变性。可以克服瑞丽限。

6、DML算法

利用最大似然准测，将背景噪声和接收噪声认为成大量独立的噪声源发射的，因而把噪声过程视为一平稳高斯随机白噪声过程，信号波形则假设为确定性信号，但输入波形是待估计的位置参数。而确定性最大似然估计算法中的未知参数是信号参数 $\theta$ 和噪声方差。这些未知量都是最大化似然估计得到的。可以克服瑞丽限。

7、OMP算法

压缩感知领域的贪婪算法，分解的每一步对所选择的全部原子进行正交化处理的一种算法，以达到更快的收敛速度。

上述算法会酌情在以后更新，本文主要介绍MUSIC算法。（作者刚入门，很多都不会，还请见谅orz）

2.4、MUSIC算法（多种信号分类算法）

雷达到达角估计是雷达信号处理中的一个重要问题，旨在确定来自目标的雷达信号的到达角度。雷达到达角估计算法可以分为时域方法和频域方法两种类型。其中，频域方法可以进一步分为基于阵列信号处理的方法和基于普通雷达信号处理的方法。本文会讲述基于频域方法中的MUSIC算法。

2.4.1、DoA估计

根据天线阵列的的接收信号，从而估计出单个或者多个信号源的方位信息，由于激励信号和方向图之间存在傅里叶关系，进而DoA估计可以等效为谱估计问题。

2.4.2、MUSIC基本思想

将任意阵列的输出数据的协方差矩阵进行特征分解，从而得到与信号分量相对应的信号子空间和与信号分量正交的噪声子空间。即：

$X(t)=\sum_{i=1}^rS_i(t)A(\theta_i)+N(t)$

2.4.3、为什么要用MUSIC？

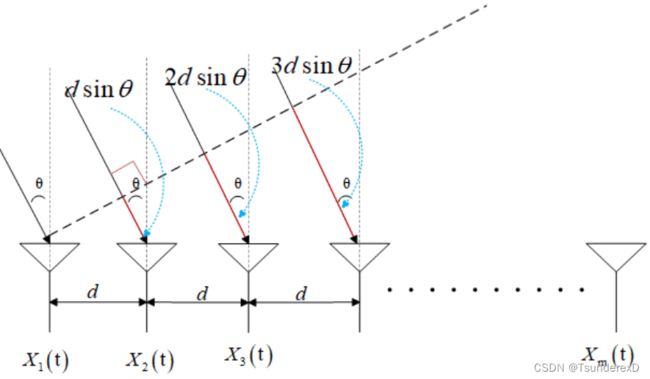
下图是一个典型的SIMO传输模型，共有M个均匀的线性接收天线，每个接收天线阵源之间相隔距离为d ，设一个信号符合远场信号模型，如下：

当只有一个发射天线TX时，也就是单发多收(SIMO)，信道图形如上图，信号到达第二个天线阵远比到达第一个天线阵元之间相隔了 $d\sin (\theta )$ 的路程。同理，第三个比第一个多了 $2d\sin (\theta )$ 的路程，即后一个阵元会比前一个阵元多走 $d\sin (\theta )$ 的路程。根据电磁波的速度为，波长为 $\lambda$ 。可以推出信号到达后一个接收天线和到达前一个接收天线的时间差为：

$\Delta \tau =\frac{d\sin (\theta )}{c}$

若信号频率为 $f_{0}$ ，可得到两个阵元之间的相位差为：

$\Delta \phi =\frac{2\pi f_{0}d\sin (\theta )}{c}=\frac{2\pi d\sin \theta }{\lambda }$

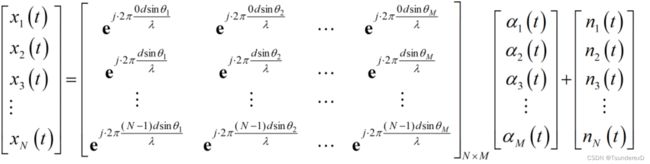
设远场发射信号为s(t)，则整个接收阵列的信号可表示为：

$\mathbf{x(t)=}\Bigg[1,\mathbf{e}^{j2\pi\frac{d\sin\theta}{\lambda}},\mathbf{e}^{j2\pi\frac{2d\sin\theta}{\lambda}},\mathbf{e}^{j2\pi\frac{3d\sin\theta}{\lambda}},\cdots,\mathbf{e}^{j2\pi\frac{(M-1)d\sin\theta}{\lambda}}\Bigg]s(t)+\boldsymbol{n}(t)$

若定义：

$A=\begin{bmatrix}1,&\text{e}^{j2\pi\frac{d\sin\theta}{\lambda}},&\text{e}^{j2\pi\frac{2d\sin\theta}{\lambda}},&\text{e}^{j2\pi\frac{3d\sin\theta}{\lambda}},\cdots,\text{e}^{j2\pi\frac{(M-1)d\sin\theta}{\lambda}}\\\end{bmatrix}$

可以得到接收信号的表达式为：

$\boldsymbol{x}\left(t\right)=\boldsymbol{A}\boldsymbol{s}\left(t\right)+\boldsymbol{n}\left(t\right)$

其中第个阵元在时刻的噪声为 $n_{i}(t)$ ，因此，只要能估计出就能波的方向。

我们假设r为反射信号常数，有这么一个公式：

$y_{1}=r*s_{1}$ $y_{2}=r*s_{1}*\phi _{1}$ $y_{3}=r*s_{1}*\phi _{2}$

其中 $y_{1}$ 为第一个RX阵元接收到的信号，其他同理，其中：

$\phi_{i} =e^{j2\pi f\frac{i*d\cos\theta }{c}}$

这其中的所有参数，除了 $\theta$ 都是已知的，因此，我们只需要将：

$\frac{y_{2}}{y_{1}}=\phi _{1}$ $\frac{y_{2}}{y_{1}}=\frac{\phi _{2}}{\phi _{1}}$ 后续同理

这样可以求出所有的 $\phi$ ，通过 $\phi$ 可以推出信源位于接受天线的方向。

看起来是不是很简单？确实，看起来确实很简单，但是这是很理想的情况，信源不可能只发送一种信号，在实际中，还会伴有各种各样的反射。这样的话，接收信号y不仅仅是简单的 $y_{1}=r*s_{1}$ ，其中还会有其他反射的信号，这里假设另外一个反射的信号为

$y_{1}=r_{1}*s_{1}+r_{2}*s_{2}$

$y_{2}=r_{1}*s_{1}*\phi _{1}+r_{2}*s_{2}*\phi _{2}$

那么

$\frac{y_{2}}{y_{1}}=\frac{r_{1}*s_{1}*\phi _{1}+r_{2}*s_{2}*\phi _{2}}{r_{1}*s_{1}+r_{2}*s_{2}}$

显而易见，二者相除什么也得不出来，在这种情况下（也可以成为多径干扰），MUSIC算法就是用来解决这个问题的。

2.4.4、MUSIC算法原理

假设空间中存在M个不同方向的信号，入射到由N个天线单元构成的均匀直线阵上，第i个1信号源的方向为 $\phi _{i}$ (i=1,2...,M)。第i个信号源的信号为 $\alpha _{i}(t)$ ，假设M。在窄带远场条i按下，第n个天线单元的输出信号 $x_{n}(t)$ 可表示为

将N个天线的输出信号表示为向量形式x(t)，则上式可以归纳成：

$\mathbf{x}(t)=\mathbf{S}\alpha(t)+\mathbf{n}(t)$

其中，S为阵列的流型矩阵，矩阵规模为NxM，具体可表示为M个不同方向对应的阵列的导向矢量。

$S=\begin{bmatrix}s(\theta_1), & s(\theta_2), & s(\theta_3),...,s(\theta_{D})\end{bmatrix}$ （列向量捏）

由于M

我们现在假设一个前提，不同信号源的信号之间是相互正交的，噪声和信号也是正交的（理想条件），则输出信号的协方差矩阵为：

$\begin{aligned} \text{R}& =\operatorname{E}[\mathbf{x}(t)\mathbf{x}(t)^H] \\ &=\mathrm{E}[\mathbf{S}\alpha(t)\alpha(t)^H\mathbf{S}^H+\mathbf{n}(t)\mathbf{n}(t)^H] \\ &=\mathbf{SAS}^H+\sigma^2\mathbf{I} \\ &=\mathbf{R}_S+\sigma^2\mathbf{I} \end{aligned}$

其中， $\sigma^2$ 为噪声的功率， $\mathbf{I}$ 为单位矩阵，A为不同信号源之间的协方差矩阵。由于不同信号源之间是相互正交的关系，因此A为正定对角矩阵。

$\mathbf{A}=\begin{bmatrix}\operatorname{E}[|\alpha_1(t)|^2]&\cdots&\cdots&\cdots\\\cdots&\operatorname{E}[|\alpha_2(t)|^2]&\cdots&\cdots\\\cdots&\cdots&\cdots&\cdots\\\cdots&\cdots&\cdots&\operatorname{E}[|\alpha_M(t)|^2]\end{bmatrix}$

由于信号协方差矩阵Rs的规模为 $N\times N$ ，秩为， $R_{s}$ 存在N-M个特征值为0的特征向量，令这种特征向量为 $q_{m}$ ,则：

上述推论说明， $R_{s}$ 的特征值为0的时候，对应特征向量 $q_{m}$ 与信号源对应的M个导向矢量均是正交的关系，令 $R_{s}$ 的N-M个特征值为0时对应的特征向量构成矩阵 $Q_{n}$ ，其规模为Nx(N-M)时，

$\mathbf{S}^H\mathbf{Q}_n=0$

即

$s(\theta )^{H}Q_{n}=0$

由上式可以清晰的看出MUSIC的原理，( $s(\theta )^{H}$ 是1xM， $Q_{n}$ 是Mx(M-N) )同时由于S的列向量和信源发射信号的方向相对应，则更可以根据这一特性估计信号源的方向。

则MUSIC算法的谱估计公式为：

$P_{\mathrm{MUSIC}}(\phi)=\frac{1}{\left|\left|\mathbf{Q}_{n}^{H}\mathbf{s}(\theta )\right|\right|^{2}}=\frac{1}{s^{H}(\theta )Q_{n}Q_{n}^{H}s(\theta )}$ $\theta \in [-\pi ,\pi ]$

当信源的方向与其中 $\theta$ 相同时，分母为0，这样MUSIC谱即为无穷大，因此，MUSIC谱的尖峰数与信源数相同，尖峰对应的角度方向即为信源对应的角度方向。

在实际工程中，由于数据长度不可能为无限长，因此会用相关矩阵的估计 $\hat{\boldsymbol{R}}$ 来代替协方差矩阵 ${\boldsymbol{R}}$ 。即：

$\hat{\boldsymbol{R}}=\frac{1}{N}\sum_{i}^{N}x_{i}x_{i}^{\mathrm{H}}$

对估计矩阵 $\hat{\boldsymbol{R}}$ 进行特征值分解，便可以得到i信号子空间的估计矢量矩阵 $\hat{\boldsymbol{S}}$ ,根据信号的特征值大小对信号的特征向量进行从大到小的重新排列，便可以得到噪声信号子空间的估计矢量 $\hat{\boldsymbol{Q}_{n}}$ 。同时，在实际工程中，还具有噪声的影响，一般信号子空间导向矢量 $s(\theta )$ 与噪声子空间 $\hat{\boldsymbol{Q}_{n}}$ 不可能完全正交，也即：

$P_{mn}\left(\theta\right)=\frac1{\boldsymbol{s}\left(\theta\right)^\mathrm{H}\hat{\boldsymbol{Q}}_{N}\hat{\boldsymbol{Q}}_{N}^\mathrm{H}\boldsymbol{s}\left(\theta\right)}\neq 0$

于是MUSIC谱

$P_{mn}\left(\theta\right)=\frac1{\boldsymbol{s}\left(\theta\right)^\mathrm{H}\hat{\boldsymbol{Q}}_{N}\hat{\boldsymbol{Q}}_{N}^\mathrm{H}\boldsymbol{s}\left(\theta\right)}$

在分达到最小值的时候，MUSIC谱达到最大值，即信号源的方向。

2.4.5、如何计算噪声子空间 $Q_{n}$ ？

通过记录多组阵列输出信号快拍，可以计算出输出信号协方差矩阵的近似值

$\mathbf{R}=\frac1K\sum_{k=1}^K\mathbf{x}_k\mathbf{x}_k^H$

那么，如何根据输出信号的协方差矩阵估计出信号协方差矩阵 $R_{s}$ 对应的特征值为 0 的特征向量矩阵 $Q_{n}$ 呢

对 $R_{s}$ 的任意特征向量 $q_{m}\in Q$ ，有

$\begin{aligned} \mathbf{R}_{S}\mathbf{q}_{m}=\lambda_{m}\mathbf{q}_{m} \\ \Rightarrow\mathbf{R}\mathbf{q}_m& =\mathbf{R}_S\mathbf{q}_m+\sigma^2\mathbf{I}\mathbf{q}_m \\ &=(\lambda_m+\sigma^2)\mathbf{q}_m \end{aligned}$

因此，信号写反差矩阵 $R_{s}$ 的特征值 $\lambda _{m}$ 对应的特征向量与输出信号协方差矩阵R的特征值 $\lambda _{m}+\sigma ^{2}$ 对应的特征向量相同。

R的特征分解可以表示为：

$\begin{aligned} \text{R}& :=\mathbf{Q}(\boldsymbol{\Lambda}+\sigma^2\mathbf{I})\mathbf{Q}^H \\ &=\mathbf{Q}\begin{bmatrix}\lambda_1+\sigma^2&0&\ldots&0&0&\ldots&0\\0&\lambda_2+\sigma^2&\ldots&0&0&\ldots&0\\\ldots&\ldots&\ldots&\ldots&\ldots&\ldots&\ldots\\0&0&\ldots&\lambda_M+\sigma^2&0&\ldots&0\\0&0&\ldots&0&\sigma^2&\ldots&0\\\ldots&\ldots&\ldots&\ldots&\ldots&\ldots&\ldots\\0&0&\ldots&0&0&\ldots&\sigma^2\end{bmatrix}\mathbf{Q}^H \end{aligned}$

上式表明，将输出信号矩阵R进行特征分解得到的N-M个较小且相等的特征值对应的特征向量即为 $Q_{n}$ 。

2.4.6、MUSIC算法步骤

根据公式，我们可以知道，想要计算MUSIC谱，需要空间导向和矢量噪声子空间。后者很好求，那么如何求得这两个东西呢？

1、首先获得接收信号

$\mathbf{x}(k)=\mathbf{S}\alpha(k)+\mathbf{n}(k)$

然后通过公式：

$\hat{R}=\frac{1}{N}\sum_{i}^{N}x_{i}x_{i}^{\mathrm{H}}$

获得协方差矩阵估计值 $\hat{R}$

2、对估计协方差矩阵进行特征值分解，可得到公式：

$\begin{aligned}\hat{\boldsymbol{R}}&=\boldsymbol{U}\boldsymbol{\Sigma}\boldsymbol{U}^\mathrm{H}\\&=\begin{bmatrix}\boldsymbol{U}_s\boldsymbol{U}_N\end{bmatrix}\begin{bmatrix}\boldsymbol{\Sigma}_s&0\\0&\boldsymbol{\Sigma}_N\end{bmatrix}\begin{bmatrix}\boldsymbol{U}_s^\mathrm{H}\\\boldsymbol{U}_N^\mathrm{H}\end{bmatrix}\end{aligned}$

根据特征值对信号源数进行判断。（作者太懒了 Un和Qn其实是一个东西哦，就不改了）

3、将第二部获得的特征值进行从大到小的排列，得到信号子空间与噪声子空间 $\hat{Q_{n}}$ 。

4、根据公式