我曾踏足山巅，也曾跌入低谷，二者都让我受益良多——P1002 过河卒

本章的内容有以下几点：1，建立虚拟边界    2，递推    3，用数组标记障碍物。

上链接：P1002 [NOIP2002 普及组] 过河卒 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

上题干：

题目描述

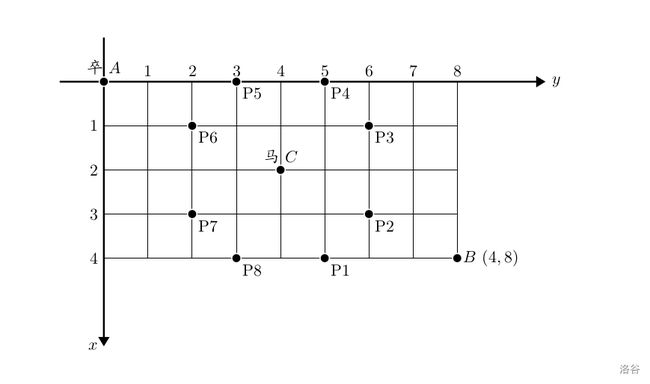
棋盘上 A 点有一个过河卒，需要走到目标 B 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 C 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，A 点 (0,0)B 点 (n,m)，同样马的位置坐标是需要给出的。

现在要求你计算出卒从 A 点能够到达 B 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 B 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

输入输出样例

输入 #1

6 6 3 3

输出 #1

6

说明/提示

对于 100% 的数据，1≤n,m≤20，0≤ 马的坐标 ≤20。

这 题的思路是这样的：

首先我们建立一个棋盘：chess[50][50].

假设没有“马拦过河卒”这个条件，那么这道题目就是简单的走方格类题目。可以用递推的方法解决。

比如说chess[2][2]代表走到（2，2）的路径数量，由于棋子只能向下和向右走，所以走到

（2，2）的前提就是走到（1，2） or （2，1） 也就是chess[2][2]=chess[1][2]+chess[2][1];

那么右：

chess[1][2]=chess[1][1]+chess[0][2];

chess[1][1]=chess[0][1]+chess[1][0]

chess[0][1]和chess[1][0]无法再分为chess[-1][0]（数组下标不能为0）

所以这个递推是有条件的，并且我们要将原点赋值为1，不然不管怎么递推结果都为。

那么好，我们现在引出了两个问题：这个递归的条件是什么，换句话说该如何使得下标不为负数。

还有一个是如果从初始值开始 f[1][1]=f[1][0]+f[0][1] ，那f[0][1],f[1][0]怎么求值，更长远的看f[n][0]怎么求值。

好现在就引入这些问题的答案：

1，虚拟边界：指的是我们可以认为将棋盘加一个虚拟边界，使得数组下标不会越界，也可以认为是将棋盘平移了。

2，怎么求f[n][0]，我们可以先加两圈虚拟边界，使得起点在f[2][2],然后初始化数组为0，再用f[2][2]+=f[2-1][2]+f[2][2-1],多了个+可以保证f[2][2]=1。

好上面的问题基本解决了，现在我们只要将“马拦过河卒”这个条件加上就行了。

怎么加效果好呢，可以建立一个标记数组，把所有马能跳到的位置都标记了，如果被标记了，就不递推这个坐标，所以到这个坐标的路径就是0，这时候我们的虚拟边界就可以使得马跳到的位置不会越界数组。

说了这么多，上代码！！！

#define _CRT_SECURE_NO_WARNINGS
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
long long chess[50][50];
int flag[50][50];//障碍标记点
int xb, yb, xm, ym;
int dx[9] = { 2,1,-1,-2,-2,-1,1,2 };
int dy[9] = { 1,2,2,1,-1,-2,-2,-1 };
int main()
{
	cin >> xb >> yb >> xm >> ym;
	xb += 3;
	yb += 3;
	xm += 3;
	ym += 3;

	for (int i = 0; i <= 8; i++)
	{
		flag[xm + dx[i]][ym + dy[i]] = 1;
	}
	if (flag[3][3] == 1)
	{
		cout << 0;
		return 0;
	}

	chess[3][3] = 1;
	for (int i = 3; i <= xb; i++)
	{
		for (int j = 3; j <= yb; j++)
		{
			if (flag[i][j])continue;
			chess[i][j] += chess[i - 1][j] + chess[i][j - 1];
		}
	}
	cout << chess[xb][yb];

}