数学模型：传染病模型

需要考虑的问题

• 描述传染病的传播过程
• 分析受感染人数的变化规律
• 预报传染病高潮到来的时刻
• 预防传染病蔓延的手段

基本方法

不需要从医学的角度分析各种传染病的特殊机理，而是按照传播过程的一般规律建立数学模型。

模型1

感染人数i随着时间t的变化率。
思考过程：病人越多，接触的人越多，感染的人越多。由此可以得到一个所需因素：病人每天接触到的人数λ。

假设：每个病人每天有效接触（足以使人治病）人数为λ

建模：$i(t+\Delta t)-i(t)=\lambda i(t)\Delta t$
由上面的模型可以得到
$\frac{di}{dt}=\lambda i$
$i(0)=i_0$
整理得出$i(t)=i_0{e}^{\lambda t}$

t→∞时得出的是i→∞，表示t趋近于无穷大时，全部的人都会得病，但是这很明显不符合实际的情况。短期可能可以使用该模型，但长期的传染病不可以使用。

模型2（SI模型）

区分已感染者（病人）和未感染者（健康人）

假设：

• 总人数N不变，病人和健康的人的比例分别为i(t),s(t)。
• 每个病人每天都有效接触人数为λ，且使接触的健康人治病。 [λ:日接触率]

建模 $N[i(t+\Delta t)-i(t)]=[\lambda s(t)]Ni(t)\Delta t$

$\frac{di}{dt}=\lambda si$

$s(t)+i(t)=1$

讲上述条件整理得到
$$\{\begin{array}{r}\frac{di}{dt}=\lambda si\\ i(0)=i_0\end{array}$$
以上的模型叫做：Logistic模型

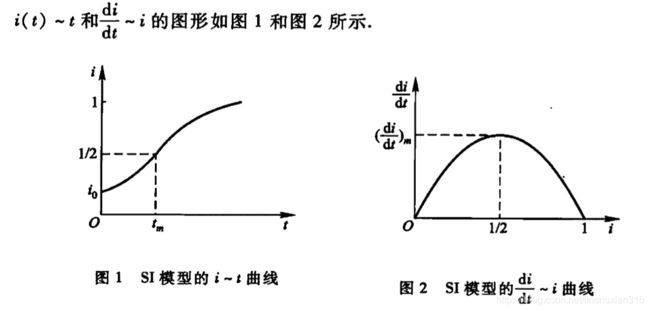
简单分析：i=0时导数为0，增长率为了0，当i=1时即全部是病人时增长率也为0，符合实际情况的假设。

此模型的解为： $\frac{1}{1+(\frac{1}{i_0}-1)e^{-\lambda t}}$

t_m是传染病高潮到来时刻

模型2的缺陷：没有考虑有的病人是可以治愈的。

模型3（SIS模型）

前提： 传染病无免疫性——病人治愈成功为健康人，健康人可再次感染。
新增假设：

• 病人每天被治愈的比例为μ，μ为日治愈率。

建模：$N[i(t+\Delta t)-i(t)]=\lambda Ns(t)i(t)-\mu Ni(t)\Delta t$
其中$\mu Ni(t)\Delta t$是治愈的人数

整理得
$$\{\begin{array}{rl}\frac{di}{dt}& =\lambda i(1-i)-\mu i\\ i(0)& =i_0\end{array}$$

$用\sigma =\lambda /\mu 代入上面的式子得出\frac{di}{dt}=-\lambda i[i-(1-\frac{1}{\sigma })]$
其中λ表示日接触率，1/μ表示感染期[μ表示一个人一天内被治好的概率，1/μ表示平均得多久的病才会被治好]，σ表示一个感染期内每个病人的有效接触人数，称为接触数。

模型4（SIR模型）

前提： 传染病有免疫性——病人治愈后立即移除感染系统，称为移出者。
假设

• 总人数N不变，病人、健康人和移出者的比例分别为i(t),s(t),r(t).
• 病人的日接触率λ，日治愈率μ，接触数σ=λ/μ

建模
第一个方程还是前面模型3中治愈的方程:
$$N[i(t+\Delta t)-i(t)]=\lambda Ns(t)i(t)-\mu Ni(t)\Delta t$$
第二个方程是健康人的变化，健康人和病人之间的变化关系：
$$N[s(t+\Delta t)-s(t)]=-\lambda Ns(t)i(t)-\mu Ni(t)\Delta t$$
即可得到
$$\{\begin{array}{rl}\frac{di}{dt}& =\lambda si-\mu i\\ \frac{ds}{dt}& =-\lambda si\\ i(0)& =i_0\\ s(0)& =s_0\end{array}$$

此方程没有解析解，但观察上面的两个微分方程，发现右边都与t无关，两者相除左边消去dt，只研究两者变量之间的关系：
$i_0+s_0\approx 1（通常r(0)=r_0很小）$
可以先做数值计算，再在相平面上研究解析解性质。

设λ=1，μ=0.3，i₀=0.02，s₀=0.98，用MATLAB计算作图i(t),s(t)及i(s)。
相轨线的分析：
$$N[s(t+\Delta t)-s(t)]=-\lambda Ns(t)i(t)-\mu Ni(t)\Delta t$$

即可得到
KaTeX parse error: Expected group after '\right' at end of input: …ligned} \right

求解出相轨线为
$$i(s)=(s_0+i_0)-s+\frac{1}{\sigma }ln\frac{s}{s_0}$$
可以发现i是由一个最大值，在s=1/σ的时候达到。

• s₀＞1/σ时i(t)先上升后下降至0 [传染病蔓延]
• s₀＜1/σ时i(t)单调降至0 [传染病蔓延]

传染病不蔓延的条件——s₀＜1/σ

预防传染病蔓延的手段：

• 提高阈值：降低σ(λ/μ)
  →降低λ（日接触率）：隔离
  →提高μ：提高医疗水平
• 降低s₀
  s₀+i₀+r₀=1，i₀为感染比例，使得s₀下降的方法就应该为提高r₀，也就是进行群体免疫（打疫苗）。

通过具体数据观察病情蔓延变化：

σ的估计
$$(s_0+i_0)-s_{\infty }+\frac{1}{\sigma }ln\frac{s_{\infty }}{s_0}$$
刚刚开始的时候忽略i₀，估计σ
$$\sigma =\frac{ln{s}_0-ln{s}_{\infty }}{s_0-s_{\infty }}$$

被传染者比例估计