栈与队列

 数据结构、算法总述：数据结构/基础算法 C/C++_禊月初三的博客-CSDN博客

栈

定义：

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。
压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
出栈：栈的删除操作叫做出栈。出数据也在栈顶。

#include
#include
#include
#include

typedef int STDataType;

typedef struct Stack
{
	STDataType* a;
	int top;		// 标识栈顶位置的
	int capacity;
}ST;

void STInit(ST* pst);
void STDestroy(ST* pst);

// 栈顶插入删除
void STPush(ST* pst, STDataType x);
void STPop(ST* pst);
STDataType STTop(ST* pst);

bool STEmpty(ST* pst);
int STSize(ST* pst);

实现：

void STInit(ST* pst)
{
	assert(pst);

	pst->a = NULL;
	pst->capacity = 0;

	// 表示top指向栈顶元素的下一个位置
	pst->top = 0;

	// 表示top指向栈顶元素
	//pst->top = -1;
}

void STDestroy(ST* pst)
{
	assert(pst);

	free(pst->a);
	pst->a = NULL;
	pst->top = pst->capacity = 0;
}

// 栈顶插入删除
void STPush(ST* pst, STDataType x)
{
	assert(pst);

	if (pst->top == pst->capacity)
	{
		int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
		STDataType* tmp = (STDataType*)realloc(pst->a, sizeof(STDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}

		pst->a = tmp;
		pst->capacity = newcapacity;
	}

	pst->a[pst->top] = x;
	pst->top++;
}

void STPop(ST* pst)
{
	assert(pst);
	// 不为空
	assert(pst->top > 0);

	pst->top--;
}

STDataType STTop(ST* pst)
{
	assert(pst);
	// 不为空
	assert(pst->top > 0);

	return pst->a[pst->top - 1];
}

bool STEmpty(ST* pst)
{
	assert(pst);

	return pst->top == 0;
}

int STSize(ST* pst)
{
	assert(pst);

	return pst->top;
}

队列

定义：

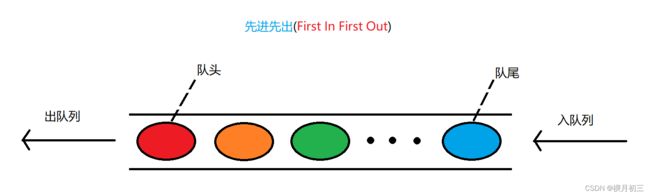
队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out)的原则。

入队列：进行插入操作的一端称为队尾。

出队列：进行删除操作的一端称为队头。

#include
#include
#include
#include

typedef int QDataType;
typedef struct QueueNode
{
	QDataType val;
	struct QueueNode* next;
}QNode;

typedef struct Queue
{
	QNode* phead;
	QNode* ptail;
	int size;
}Queue;

void QueueInit(Queue* pq);
void QueueDestroy(Queue* pq);
void QueuePush(Queue* pq, QDataType x);
void QueuePop(Queue* pq);
QDataType QueueFront(Queue* pq);
QDataType QueueBack(Queue* pq);
bool QueueEmpty(Queue* pq);
int QueueSize(Queue* pq);

 实现：

void QueueInit(Queue* pq)
{
	assert(pq);
	pq->phead = pq->ptail = NULL;
	pq->size = 0;
}

void QueueDestroy(Queue* pq)
{
	assert(pq);

	QNode* cur = pq->phead;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}

	pq->phead = pq->ptail = NULL;
	pq->size = 0;
}

void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);

	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		return;
	}

	newnode->val = x;
	newnode->next = NULL;

	if (pq->ptail == NULL)
	{
		pq->ptail = pq->phead = newnode;
	}
	else
	{
		pq->ptail->next = newnode;
		pq->ptail = newnode;
	}

	pq->size++;
}

void QueuePop(Queue* pq)
{
	assert(pq);
	// 
	assert(pq->phead);

	QNode* del = pq->phead;
	pq->phead = pq->phead->next;
	free(del);
	del = NULL;

	if (pq->phead == NULL)
		pq->ptail = NULL;

	pq->size--;
}

QDataType QueueFront(Queue* pq)
{
	assert(pq);
	// 
	assert(pq->phead);

	return pq->phead->val;
}

QDataType QueueBack(Queue* pq)
{
	assert(pq);
	// 
	assert(pq->ptail);

	return pq->ptail->val;
}

bool QueueEmpty(Queue* pq)
{
	assert(pq);

	return pq->phead == NULL;
}

int QueueSize(Queue* pq)
{
	assert(pq);

	return pq->size;
}

---

算法模板（数组模拟）

栈

//tt表示栈顶
int stk[N], tt = 0;
//插入
stk[ ++ tt] = x;
//弹出
tt -- ;
//判断栈是否为空
if (tt > 0) not empty;
else empty;
//栈顶
stk[tt];

 题目

828. 模拟栈 - AcWing题库https://www.acwing.com/problem/content/830/

队列（普通队列）

// hh 表示队头，tt表示队尾
int q[N], hh = 0, tt = -1;
//插入
q[ ++ tt] = x;
//弹出
hh ++ ;
//判断队列是否为空
if (hh <= tt) not empty;
else empty;
//取出队头元素
q[hh];

题目

AcWing 829. 模拟队列 - AcWinghttps://www.acwing.com/activity/content/problem/content/866/ 

队列（循环队列)

// hh 表示队头，tt表示队尾的后一个位置
int q[N], hh = 0, tt = 0;
// 向队尾插入一个数
q[tt ++ ] = x;
if (tt == N) tt = 0;
// 从队头弹出一个数
hh ++ ;
if (hh == N) hh = 0;
// 队头的值
q[hh];
// 判断队列是否为空，如果hh != tt，则表示不为空
if (hh != tt)
{

}

单调栈

常见模型：找出每个数左边离它最近的比它大/小的数
int tt = 0;
for (int i = 1; i <= n; i ++ )
{
    while (tt && check(stk[tt], i)) tt -- ;
    stk[ ++ tt] = i;
}

题目：
830. 单调栈 - AcWing题库https://www.acwing.com/problem/content/832/

单调队列

常见模型：找出滑动窗口中的最大值/最小值
int hh = 0, tt = -1;
for (int i = 0; i < n; i ++ )
{
    while (hh <= tt && check_out(q[hh])) hh ++ ; // 判断队头是否滑出窗口
    while (hh <= tt && check(q[tt], i)) tt -- ;
    q[ ++ tt] = i;
}

题目：

154. 滑动窗口 - AcWing题库https://www.acwing.com/problem/content/156/