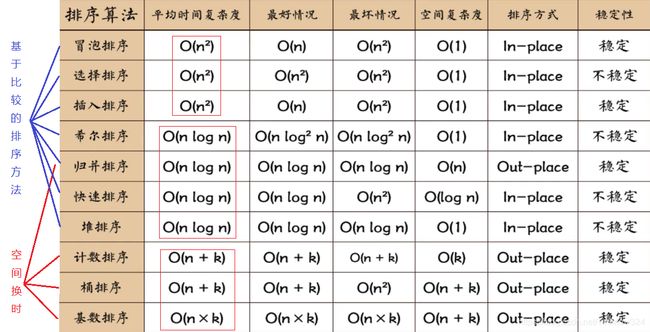
冒泡、选择、插排、希尔、归并、快速、堆排、计数、基数、桶排可视化算法
一、基于比较排序
- 冒泡排序 O(N^2)相邻的比较 将大的冒到最后
- 选择排序 O(N^2)找到最小放在前面
- 选择排序 O(N^2)让一部分有序,再遇到更小的插入
- 希尔排序 O(N logN)间隔比较 依次插入
- 快速排序 O(N logN) 找到一个中间值让左边小于等于主元,左边大于主元 重点在于分治
#快速排序单向扫描法
#快速排序双向扫描法
#快速排序三分法 - 堆排序 O(N logN) 转换成大堆或者小堆 主根一定比所有的值大或者小 和 最后一个交换 比剩下的再次转换堆
二、空间换时间排序
- 归并排序 O(N logN) 随意切割,重点在于合并
- 计数排序 O(N + K) 创建辅助空间,投影
- 基数排序 O(N + K) 个十百千万分别分桶
- 桶排序 O(N + K) 通过算法找个自己的位置,桶分类
冒泡排序
描述
将数组中最大的值冒到数组的最后,也就是说是相邻的对比
if(arr[i] > arr[i+1]){
//两个值交换
}
可视化
样例代码
public static void BubbleSort(int[] arr){
for(int i = 0;i < arr.length-1;i++){
for(int j = 0;j < arr.length-1-i;j++){//依次减少
if(arr[j] > arr[j+1]){
int item = arr[j];arr[j] = arr[j+1];arr[j+1] = item;
}
}
}
}
时间复杂度
i = 0 : 0 1 2 3 4 5 6 7 8
i = 1 : 0 1 2 3 4 5 6 7
i = 2 : 0 1 2 3 4 5 6
i = 3 : 0 1 2 3 4 5
i = 4 : 0 1 2 3
i = 5 : 0 1 2
i = 6 : 0 1
i = 7 : 0
i = 8 :
2/n*n-1
平均时间复杂度O(N²) 最好O(N) 最坏O(N^2)
选择排序
描述
在数组中找到最小的值放在第一个其实和冒泡排序差不多,同样是2/n*n-1
int min = i;
if(arr[min] > arr[j]){
min = i;//找到最小的
}
可视化
样例代码
public static void selectionSort(int[] arr){
for(int i = 0;i < arr.length-1;i++){
int min = i;
for(int j = i + 1;j < arr.length;j++){
if(arr[min]>arr[j]){
min = j;
}
}
int item = arr[min];arr[min] = arr[i];arr[i] = item;
}
}
时间复杂度
i = 0 : 1 2 3 4 5 6 7 8 9 9次
i = 1 : 2 3 4 5 6 7 8 9 8次
i = 2 : 3 4 5 6 7 8 9 7次
i = 3 : 4 5 6 7 8 9 6次
i = 4 : 5 6 7 8 9 5次
i = 5 : 6 7 8 9 4次
i = 6 :7 8 9 3次
i = 7 :8 9 2次
i = 8 :9 1次
2/n*n-1
平均时间复杂度O(N²) 最好O(N) 最坏O(N^2)
插入排序
描述
让前面的一部分有序,如果再遇到更小的,插入到他的位置
我们
样例代码
public static void insertSort(int[] arr){
for(int i = 1;i < arr.length;i++){
int Val = arr[i];
int index = i - 1;
while(index > -1 && arr[index] > Val){
arr[index+1] = arr[index];
index--;
}
arr[index++] = Val;
}
}
时间复杂度
插入排序从小到大依次往大循环,例如到下标为3,0………3为有序
最坏的情况的是从降序数组,变成增序数组
需要移动
i = 0 : 1 2 3 4 5 6 7 8 9
9次
i = 1 : 2 3 4 5 6 7 8 9
8次
i = 2 : 3 4 5 6 7 8 9
7次
i = 3 : 4 5 6 7 8 9
6次
i = 4 : 5 6 7 8 9
5次
i = 5 : 6 7 8 9
4次
i = 6 :7 8 9
3次
i = 7 :8 9
2次
i = 8 :9
1次
2/n*n-1
平均时间复杂度O(N²) 最好O(N) 最坏O(N^2)
希尔排序
希尔排序其实也就是插入排序的优化版
通过间隔来优化插入排序中的一个个比较
可视化,
样例代码
public static void ShellSort(int[] arr){
for(int i = arr.length/2;i > 0;i--){//间隔
for(int j = i;j<arr.length;j++){
int Val = arr[j];
int index = j - i;
while(index > -1 && arr[index] > Val){
arr[index+i] = arr[index]
index -= i;
}
arr[index+i] = Val;
}
}
}
时间复杂度
如果碰到最差的情况就是间隔1比较
到了间隔1还是没有序的,那么希尔排序对退化成O(N²)
平均时间复杂度 O(N logN) 最坏O(N log² N) 最好O(N log²N)
快速排序
描述
分治法
①划分子问题
②求子问题解
③合并子问题解
而快速排序重点在于划分上面
主要是确定一个中间值,左边小于等于主元,右边大于主元
图片中黄色是主元,绿色是小于等于主元的值,紫色是大于主元的值
样例代码
//我这里用的是双向扫描法
public static void quickSort(int[] arr,int begin ,int end){
if(begin<end){
if(end - begin + 1 <= 7){
insertSort(arr,begin,end);
}else{
int q = partition(arr,begin,end);
quickSort(arr,begin,q-1);
quickSort(arr,q+1,end);
}
}
}
static int partition(int[] arr,int begin,int end){
//三点确定法
int Mid = (begin+end)>>1;
if(arr[begin] >= arr[Mid] && arr[begin] <= arr[end]){
Mid = begin;
}else if(arr[end] <= arr[begin] && arr[end] >= arr[Mid]){
Mid = end;
}
//并将中间值和第一个值换个位置
int item = arr[Mid];arr[Mid] = arr[begin];arr[begin] = item;
int poivt = arr[begin];
int left = begin + 1;
int right = end;
while(left <= right){
while(left <= right && arr[left] <= poivt)left++;
while(left <= right && arr[right] > poivt)right--;
if(left < right){
int item = arr[left];arr[left] = arr[right];arr[right] = item;
}
}
int item = arr[begin];arr[begin] = arr[right];arr[right] = item;
return right;
}
static void insertSort(int[] arr,int begin,int end){
for(int i = begin + 1;i <= end;i++){
int Val = arr[i];
int index = i - 1;
while(index > begin-1 && arr[index] > Val){
arr[index+1] = arr[index];
index--;
}
arr[index+1] = Val;
}
}
时间复杂度
最好的情况就是每次划分都分到中间值,那么就是一般折一般
我在主元选择的地方采用了三点确定法,在递归上发现小于7个元素使用快速排序需要的时间会更长一些,所以我在递归上采用了小于7采用插入排序
平均时间复杂度 O(n log n) 最好O(n log n) 最坏O(n log n)
堆排序
具体请参考:https://blog.csdn.net/Tinknow324/article/details/104719885
将数组大堆或者小堆,然后形成的树的主根如果是大堆那么主根是最大的,小堆主根就是整个数组的最小,主根和最后一个值交换,并将剩下的节点重新大堆或者小堆
样例代码
public static void MaxHeapSort(int[] arr){//把数组转换成大堆树
int n = arr.length;
for(int i = n/2-1;i >= 0;i--){
MaxHeapFixDown(arr,i,n);
}
}
//大堆树
static void MaxHeapFixDown(int[] arr,int i,int n){
int left = 2 * i + 1;
int right = 2 * i + 2;
if(left>=n){
return;
}
int max = left;
if(right >= n){
max = left;
}else{
if(arr[left] > arr[right]){
max = left;
}else{
max = right;
}
}
if(arr[i] > arr[max]){
return;
}
int item = arr[i];arr[i] = arr[max];arr[max] = item;
MaxHeapFixDown(arr,max,n);
}
static void HeapSort(int[] arr){
MaxHeapSort(arr);
for(int i = arr.length-1;i >= 0;i--){
int item = arr[0];arr[0] = arr[i];arr[i] = item;
MaxHeapFixDown(arr,0,i)
}
}
时间复杂度
树的时间复杂度是O(n log n)
堆排的平均时间复杂度O(n log n) 最好是O(n log n) 最坏O(n log n)
归并排序
描述
归并排序同样也是使用分治法
分治法
①划分子问题
②求子问题解
③合并子问题解
归并的重点在于合并,随意的划一刀,分成两个有序,小的先走
public static void MergeSort(int[] arr,int begin,int end){
if(begin<end){
int Mid = (begin+end)>>1;
MergeSort(arr,begin,Mid);//包含中间划分到左边
MergeSort(arr,Mid+1,end);
Merge(arr,begin,Mid,end);
}
}
static void Merge(int[] arr,int begin,int Mid,int end){
int[] helper = new int[arr.length];
system.arraycopy(arr,begin,helper,begin,(end-begin)+1);
int current = begin;
int left = begin;
int right = Mid+1;
while(left<=Mid&&right<=end){
if(helper[left]<=helper[right]){
arr[current++] = helper[left++];
}else{
arr[current++] = helper[right++];
}
}
while(left<=Mid){
arr[current++] = helper[left++];
}
}
时间复杂度
平均时间复杂度O(n log n) 最好是O(n log n) 最坏O(n log n)
计数排序
描述
计数排序其实就是一个金典的空间换时间的算法
创建一个长度为数组中最大数+1长度的辅助数组
依次遍历数组中所有元素,投影到该数的下标
最后从辅助数组中返回到原数组就完成了排序

代码实现
public static void CountSort(int[] arr){
int max = maxof(arr);
int[] helper = new int[max];
for(int i=0;i<arr.length;i++){
helper[arr[i]]++;
}
int current = 0;
for(int i = 0;i<helper.length;i++){
for(int j = helper[i];j>0;i--){
arr[current++] = i;
}
}
}
static int maxof(int[] arr){
int max = arr[0];
for(int i = 1;i<arr.length;i++){
if(arr[i]>max){
max = arr[i];
}
}
}
时间复杂度
第一次计数O(N)
第一次返回O(K)
O(N+K) K是原数组中最大值
基数排序
描述
基数排序其实和桶排序,计数排序很相似
判断个十百千的大小,排序,
个位 入桶 出桶
十位 入桶 出桶
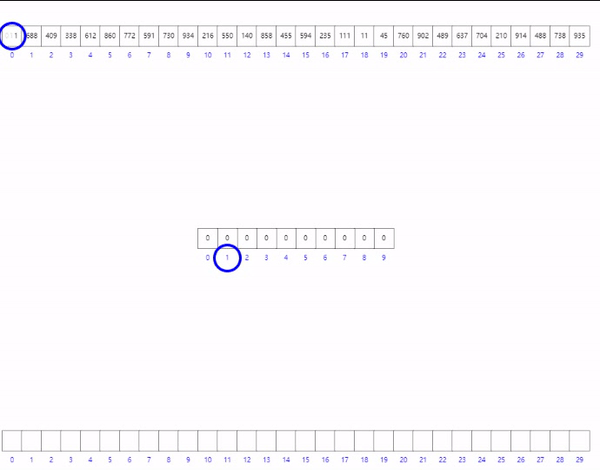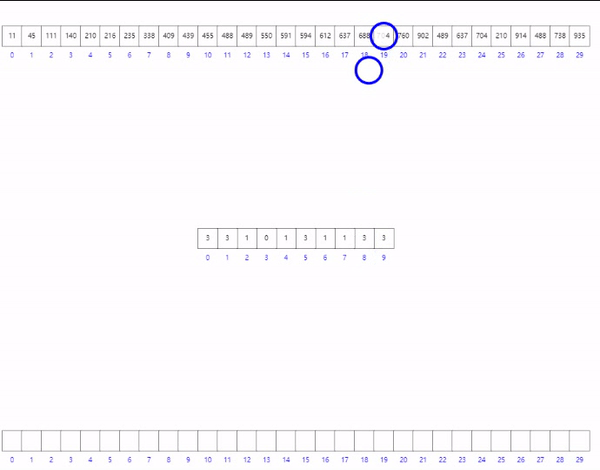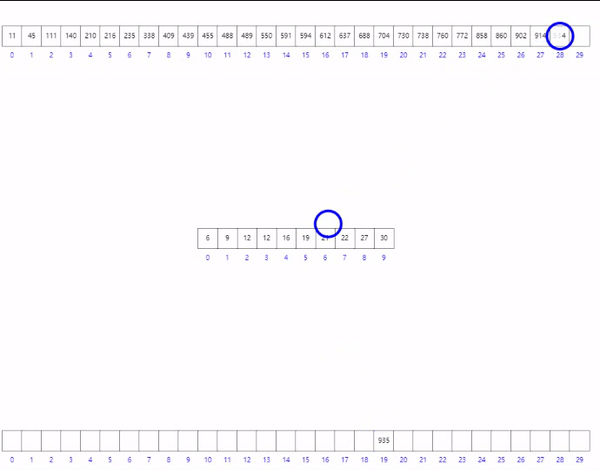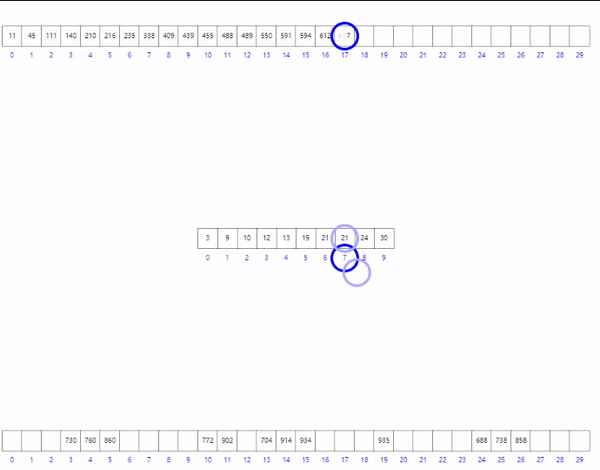
代码实现
class Radix{
private static ArrayList[] bucket = new ArrayList[10];
static{
for(int i =0;i<bucket.length;i++){
bucket[i] = ArrayList();
}
}
private static int maxof(int[] arr){
int max = arr[0];
for(int i = 1;i<arr.length;i++){
if(arr[i]>max){
max = arr[i];
}
}
}
public static void RadixSort(int[] arr){
int max = maxof(arr);
int maxbit = 0;
while(max>0){
maxbit++;
max/=10;
}
int k = 1;
while(k<=maxbit){//按照k入桶,比较maxbit次
Sort(arr,k);
}
}
private static void Sort(int[] arr,int k){
for(int i = 0;i < arr.length;i++){//根据k位依次入桶
tobucket(arr[i],getbitVal(arr[i],k));
}
int current = 0;
for(int i = 0;i < bucket.length;i++){
for(int j = 0;j < bucket[i].size();j++){
arr[current++] = (int)bucket[i].get(j);
}
}
clear(bucket);//每次出桶之后一定要清除原来的元素
}
private static int getbitVal(int data,int k){
return data%Math.pow(10,k)/Math.pow(10,k-1);//从右往左取k位
}
private static void tobucket(int data,int k){
switch(k){
case 0 :bucket[0].add(data);break;
case 1 :bucket[1].add(data);break;
case 2 :bucket[2].add(data);break;
case 3 :bucket[3].add(data);break;
case 4 :bucket[4].add(data);break;
case 5 :bucket[5].add(data);break;
case 6 :bucket[6].add(data);break;
case 7 :bucket[7].add(data);break;
case 8 :bucket[8].add(data);break;
case 9 :bucket[9].add(data);break;
}
}
private static void clear(ArrayList[] data){
for(int i = 0;i < data.length;i++){
data[i].clear();
}
}
}
时间复杂度
入桶 O(N) 出桶 O(N)
需要maxbit次入桶出桶
平均复杂度 O(N * K) 最坏O(N * K) 最好O(N * K)
桶排序
描述
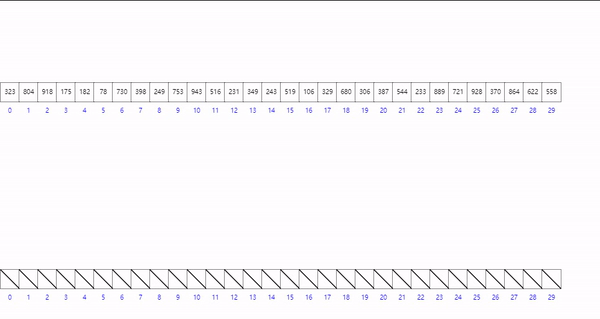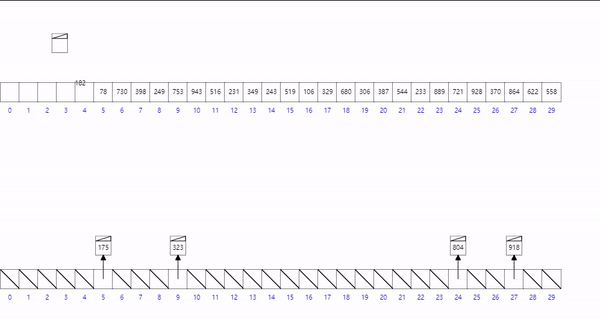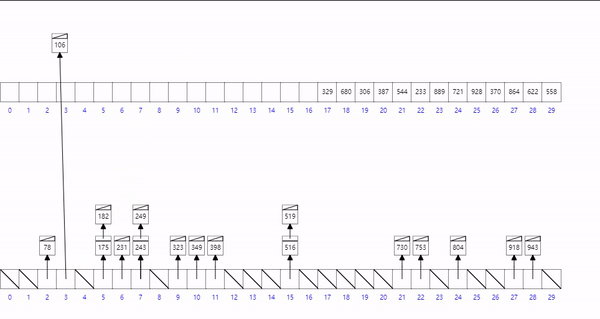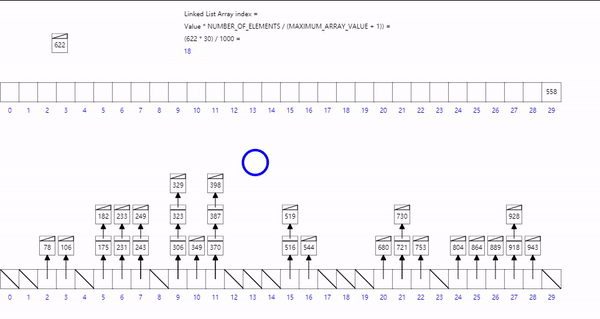
通过算法找到桶的位置,并让值在桶在有序
( Value * bucket_Length ) / array_max_Value + 1
样例代码
public class BucketSort {
private static ArrayList[] bucket;
private static int maxof(int[] arr){
int max = arr[0];
for(int i = 1;i<arr.length;i++){
if(arr[i]>max){
max = arr[i];
}
}
}
public static void BucketSort(int[] arr) {
int len = arr.length;//桶长
int arrmax = MaxOf(arr) + 1;//数组中最大值+1
//桶初始化
bucket = new ArrayList[len];
for(int i = 0;i < bucket.length;i++) {
bucket[i] = new ArrayList();
}
//入桶( Value * bucket_Length ) / array_max_Value + 1
for (int i = 0; i < arr.length; i++) {
toBucket(arr[i],(arr[i]*len)/arrmax);
}
//出桶
int current = 0;
for (int i = 0; i < bucket.length; i++) {
for (int j = 0; j < bucket[i].size(); j++) {
arr[current++] = (int)bucket[i].get(j);
}
}
}
//数组找到在桶中的位置
private static void toBucket(int data,int k) {
if(bucket[k].size() > 0) {//列表中有数据时
for (int i = 0; i < bucket[k].size(); i++) {//遍历列表中所有的元素
if(data <= (int)bucket[k].get(i)) {//插入的值小于等于当前值插入
bucket[k].add(i, data);
break;
}
}
}else {
bucket[k].add(data);
}
}
}