常见排序算法集合(快速排序、归并排序、插入排序、冒泡排序、选择排序、希尔排序、堆排序)

常用的排序算法

在C++里可以通过std::sort()进行快速排序，但是熟悉各种排序算法可以加深自己对算法的基本理解。常用的排序算法包括：快速排序、归并排序、插入排序、冒泡排序、选择排序、希尔排序、堆排序。

---

---

选择排序：初始序列中找到最小元素，放在序列最起始位置作为已排序序列。从剩余元素中查找最小元素，放在已排序数组最后。直到所有元素排列完毕。

void select(int arr[],int len) 
{
    for (int i = 0;i < len - 1;i++)
    {
        int min = i;
        for (int j = i + 1; j < len; j++)//查找未排序元素 
        {
            if (arr[j] < arr[min])//找到目前最小值 
            {
                min = j;    //记录最小值
            }
        }
        swap(arr[min],arr[i]);
    }
}

---

冒泡排序：从头开始依次比较相邻的两个元素，如果后面元素比前面大，交换两元素。本次循环完毕之后再次从头开始扫描，直到某次扫描中没有元素交换，说明每个元素都有序。

void BubbleSort(int arr[],int len)
{
    for (int i = 0;i < len - 1;i++)
    {
        bool sorted = true;
        for (int j = 0; j < len - 1 - i; j++)
        {
            if (arr[j] > arr[j + 1])
            {
                swap(arr[j], arr[j + 1]);
                sorted = false;
            }
        }
        if (sorted) { break; }
    }
}

---

插入排序：每插入一个数都要将它和之前的已经完成排序的序列进行重新排序，也就是要找到新插入的数对应原序列中的位置。也就是说，每插入一个数都要对原来排序好的部分进行重新排序。

void InsertSort(int arr[],int len)
{
    
    int preIndex = 0, current = 0;
    for (int i = 1; i < len; i++) 
    {
        preIndex = i - 1;
        current = arr[i];
        while (preIndex >= 0 && arr[preIndex] > current) 
        {
            arr[preIndex + 1] = arr[preIndex];
            preIndex--;
        }
        arr[preIndex + 1] = current;
    }
}

---

希尔排序：希尔排序基于插入排序，是记录按下标的一定值分组，分组后的子数组进行插入排序，使规定的值逐级减少，当值减少到1时，整个文件被分为一组算法结束。

void ShellSort(int arr[],int len)
{
    //gap为初始增量
    for (int gap = len / 2;gap > 0;gap /= 2) 
    {
        
        for (int i = gap; i < len; i++) 
        {
            int current = arr[i];
            int j = 0;
            for (j = i - gap; j >= 0 && arr[j] > current; j -= gap) 
            {
                arr[j + gap] = arr[j];
            }
            arr[j + gap] = current;
        }
    }
}

---

堆排序：堆排序是利用堆的数据结构所设计的一种排序算法。利用堆顶记录的是最大数(最小数)这一特性，使得每次从无序中选择最大记录(最小记录)。

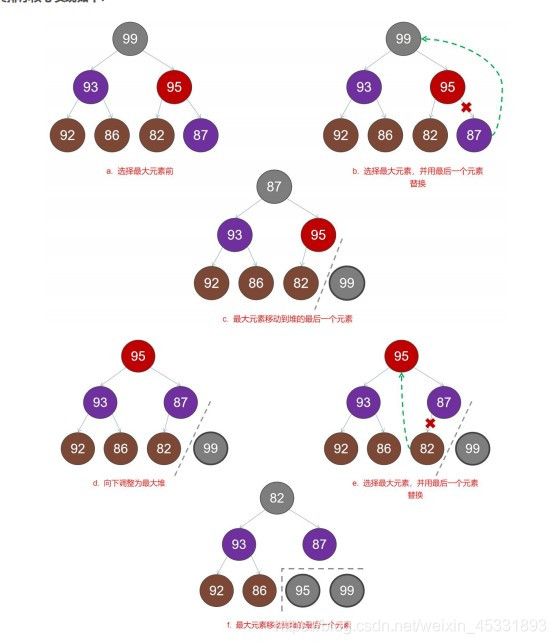
/*将当前的节点和子节点调整成最大堆*/
void adjustDown(Heap& heap, int index) {
    int cur = heap.arr[index];
    //当前待调整的节点 
    int parent, child; 
/*判断否存在大于当前节点子节点，如果不存在 ，则堆本身是平衡的，不 需要调整； 
如果存在，则将最大的子节点与之交换，交换后，如果这个子节点还有子节 点，
则要继续 按照同样的步骤对这个子节点进行调整 */
    for (parent = index; (parent * 2 + 1)<heap.size; parent = child) 
    { 
        child = parent * 2 + 1; 
        //取两个子节点中的最大的节点 
        if (((child + 1)<heap.size) && (heap.arr[child]<heap.arr[child + 1])) 
        { 
            child++;
        }
        //判断最大的节点是否大于当前的父节点
        if (cur >= heap.arr[child])
        {//不大于，则不需要调整，跳出循环 
            break; 
        }else
        {//大于当前的父节点，进行交换，然后从子节点位置继续向下调 整
            heap.arr[parent] = heap.arr[child];
            heap.arr[child] = cur; }
    }
}
/* 实现堆排序 */ 
void heapSort(Heap& heap) {
    if (heap.size < 1) return;
    while (heap.size > 0) {
        int tmp = heap.arr[0];
        heap.arr[0] = heap.arr[heap.size - 1];
        heap.arr[heap.size - 1] = tmp;
        heap.size--;
        adjustDown(heap, 0);
        // 向下执行堆调整 
    }
}

---

归并排序：归并排序利用分治法的思想：将待排序序列A分为两个子序列，再持续上述操作，直到每个子序列只含有一个元素(此时一个元素必定有序)，根据分解的步骤向上操作对每一个子序列排序，将排序的两个子序列从首元素开始将较小元素移入新序列中，最后合成整个序列。

void mergeAdd(int arr[],int left,int mid,int right,int *temp) 
{
    int i = left;//指向左边数组最小的元素位置
    int j = mid;//指向右边数组最小的元素位置
    int k = left;//临时数组的下标
    while(i < mid && j <= right)
    {
        if (arr[i] < arr[j]) {
            temp[k++] = arr[i++];
        }
        else {
            temp[k++] = arr[j++];
        }
    }
    while (i < mid) {
        temp[k++] = arr[i++];
    }
    while (j <= right) 
    {
        temp[k++] = arr[j++];
    }
    //把temp中的内容拷贝到arr数组中
    memcpy(arr + left, temp + left, sizeof(int) * (right - left + 1));
}
//归并排序。temp是临时数组，大小与排序数组相等
void mergeSort(int arr[],int left,int right,int *temp)
{
    int mid = 0;
    if (left < right) 
    {
        mid = left + (right - left) / 2;
        mergeSort(arr,left,mid,temp);
        mergeSort(arr, mid + 1, right, temp);
        mergeAdd(arr, left, mid + 1, right, temp);
    }
}

---

快速排序：选定一个基准数然后利用这个基准数将数组数据分为两个部分，大于基准数的放一边，小于基准数的放一边。继续对基准数的两侧未排序的数据进行分治法进行细分处理，直到整个序列有序。
待排序数组：

int partition(int arr[], int low, int high)
{
    int i = low;
    int j = high;
    int base = arr[low];
    if (low < high)
    {
        while (i < j)
        {
            while (i < j && arr[j] >= base)
            {
                j--;
            }
            if (i < j)//右边已经找到小于基数的数
            {
                arr[i++] = arr[j];
            }
            while (i < j && arr[i] < base)
            {
                i++;
            }
            if (i < j) //左边找到大于基数的数
            {
                arr[j--] = arr[i];
            }
        }
        arr[i] = base;
    }
    return i;
}
void QuickSort(int *arr,int low,int high)//实现快速排序 
{
    if (low < high) 
    {
        int index = partition(arr, low, high);
        QuickSort(arr, low, index - 1);
        QuickSort(arr, index + 1, high);
    }
}

推荐一个算法可视化网站。https://visualgo.net/zh 网站中包括许多算法的实现过程，对于理解数据结构算法个人感觉能起到很好的作用。
上述代码全都是我个人测试通过的。如果里面有什么错误可以在下面评论或私聊告诉我。