Java语言实现堆的实现，插入删除

二叉堆

原文章地址: 堆
二叉堆像二叉查找树一样，也含有两个性质，即结构性和堆序性，对堆的一种操作可能破坏这两个性质的一个，因此堆的操作必须到堆的所有性质都被满足才能终止

首先明确，堆必须是完全二叉树，不是完全二叉树的结构不能被称为堆

特殊结构

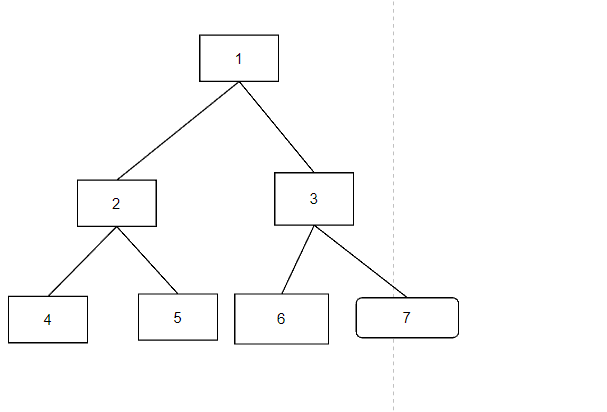
前面我们提到，这个堆必须是完全二叉树，那么堆的子父节点之间会存在一些关系，对于任意元素节点i，他的左儿子在位置2i上面，比如下面的数据2，其顺序为2，他的左儿子4在位置4上面，右儿子为2i+1

那么到这里，其实我们可以仅仅根据一个节点的位置就可以得到其子节点的位置，那么现在就不需要链表来指明下一个节点的地址了，只需要根据数组的下标即可

基本堆操作

堆的实现

class Heap {
    //代表当前堆的大小
    private int currentSize;
    //代表堆的数组
    private int[] array;
}

插入实现

当我们插入一个树的时候，需要在下一个位置创建一个节点，而该节点并不能破坏堆结构的性质，如果破坏了堆结构的性质，那么就需要我们进行元素的调换

public void insert(int x) {
    //如果当前指针指向了这个数组最终的位置，那么堆已经满了
    if (currentSize == array.length - 1) {
        System.out.println("堆已经满了,现在进行扩容");
        enlargeArray(array.length * 2 + 1);
    }
    currentSize++;
    array[currentSize] = x;
    //如果堆没有满，那么进行判断该元素的插入是否破坏了性质,此时要求根节点小于左右子节点
    //此时进行堆的判断的时候，如果根节点从数组的0开始，那么左节点的值为2i+1，右节点的值为2i+2，假设此时节点为x，那么i=(x-1)/2
    for (int i = currentSize; i > 0; i = (i - 1) / 2) {
        //得到父节点
        int temp = array[(i - 1) / 2];
        if (temp > array[i]) {
            array[(i-1)/2]=array[i];
            array[i]= temp;
        } else {
            break;
        }
    }

}

/**
 * @param x 表示数组扩容的大小
 */
public void enlargeArray(int x) {
    array = Arrays.copyOf(array, x);
}

class Test {
    public static void main(String[] args) {
        Heap heap = new Heap(9, new int[]{13, 21, 16, 24, 31, 19, 68, 65, 26, 32,0,0,0});
        //现在我需要插入14，而且必须满足堆的性质
        heap.insert(14);
        System.out.println(Arrays.toString(heap.getArray()));

    }
}

删除节点

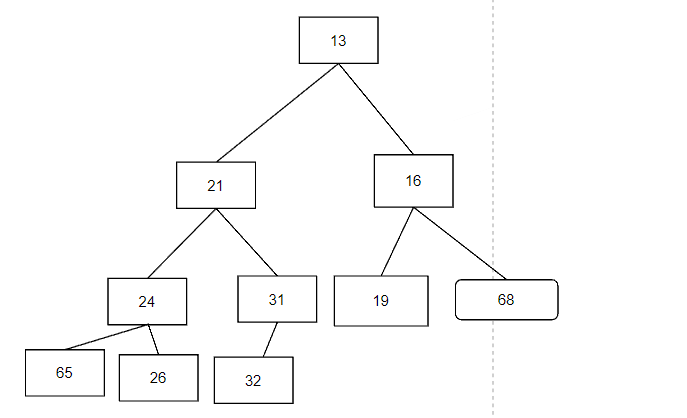
对于堆的操作，删除节点其实是删除根节点，堆又称为优先队列，适用于程序中作业优先调用的策略，那么对于上面的节点，现在删除13，而根节点空余出来，现在最简单保持结构的方法是，是将最后得到一个节点调用该位置，但是这样可能会造成顺序性的错误，那么现在为了满足堆的性质，我们将14或者16其中一个较小元素调用到上面，但是会发现下面又会得到一个空穴，那么依次调用直到完成符合的顺序，但是注意，每一次调换的时候我们都检测一边，是否可以将该队列的最后一个节点填入到空间中，一旦可以的话，那么向后就不要在进行位置替换了，此时直接结束便可以

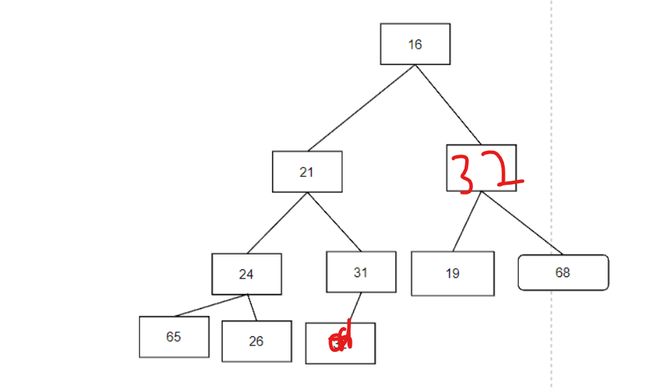
第一步，比较13节点的左右节点，发现16比较小，将16提交上去，而我们最初调整到头的32移动到下一个空穴

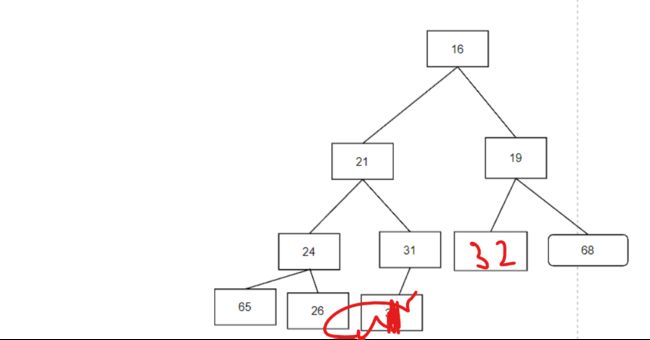
比较子节点的19与68，将19提交，比较32与19，将19填入位置，32下移动

此时发现到了最终的末尾，将32填入其中

public int deleteMin() {
        if (currentSize < 0) {
            throw new RuntimeException("堆已经为空");
        }
        //第一个便是最小元
        int minItem = array[0];
        //此时将末尾的值调度到最前面来
        array[0] = array[currentSize];
        percolateDown(0);
        return array[0];

    }

    public void percolateDown(int hole) {
        int child;
        int temp = array[hole];
        for (; hole * 2 + 1 <= currentSize; hole = child) {
            //得到左节点
            child = 2 * hole + 1;
            //如果右节点小于左节点
            if (child != currentSize && array[child + 1] < array[child]) {
                child++;
            }
            if (array[child] < temp) {
                array[hole] = array[child];
            } else {
                break;
            }
        }
        array[hole] = temp;
        //结束之后将值置空，同时堆大小-1
        array[currentSize] = 0;
        currentSize--;
    }

调整堆

堆的构建拥有两个过程，一个是挨个插入形成堆O(Nlogn)，另外一个是在一个完全二叉树的基础上调整为一个堆

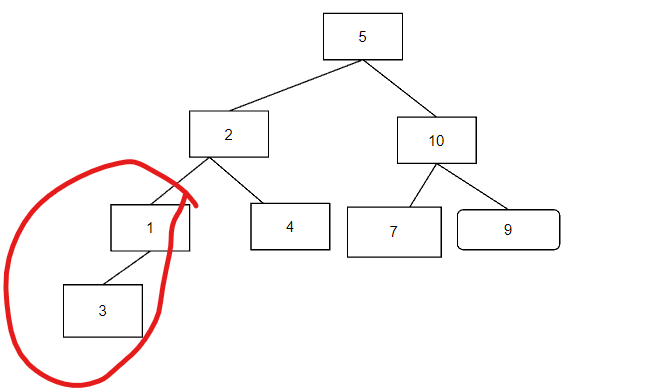
下面是一个初始的二叉树，要将这个树构建成为一个堆

第一步，比较最底层的叶子节点，1 3符合小顶堆

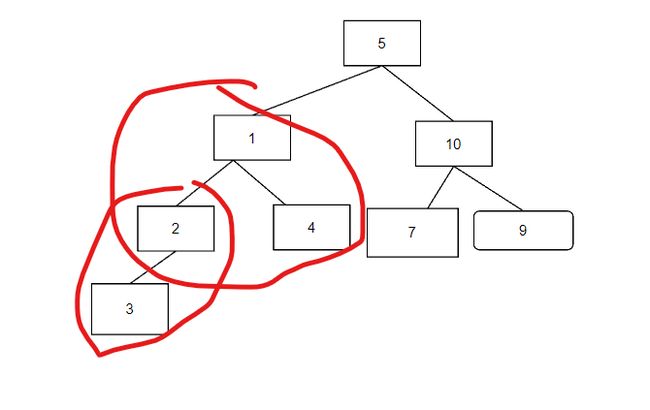
第二部，比较214节点，不符合小顶堆，将1替换上去，同时再次比较23是否符合小顶堆

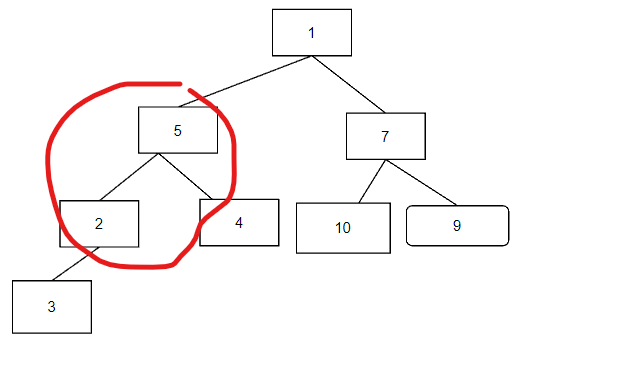
第三步，比较1079是否符合，并进行调整

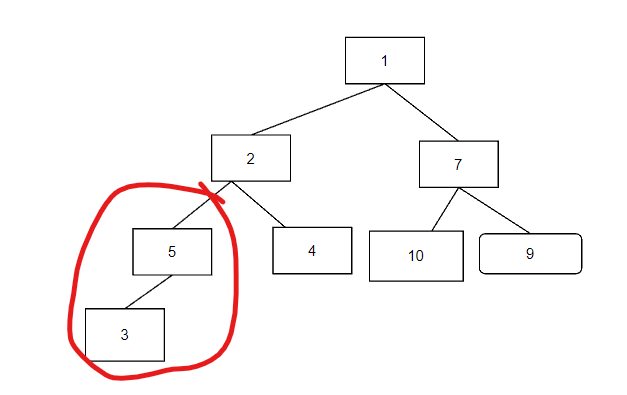
第四步比较517，进行调整，同时比较524，进行调正，并且比较53，进行调整

public void buildHeap(int[] array) {
        //现在需要从最底层的叶子节点的根节点开始调整
        for (int i=currentSize/2;i>0;i--){
            percolateDown(i);
        }
    }
public void percolateDown(int hole) {
        int child;
        int temp = array[hole];
        for (; hole * 2 + 1 <= currentSize; hole = child) {
            //得到左节点
            child = 2 * hole + 1;
            //如果右节点小于左节点
            if (child != currentSize && array[child + 1] < array[child]) {
                child++;
            }
            if (array[child] < temp) {
                array[hole] = array[child];
            } else {
                break;
            }
        }
        array[hole] = temp;
    }