四象限分析案例

四象限分析代码

先上代码

import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
#生成图表之前明确设置一个交互式框架
matplotlib.use('Qt5Agg')
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import MinMaxScaler

# 读取文件  #处理event文本信息  # 删除带有NaN值的行  # 提取特征（属性）和目标变量
# 创建MinMaxScaler对象 # 归一化特征 # 创建线性回归模型 # 拟合模型 #使用了所有的数据去拟合就不在此检验模型可靠性了
# 获取回归系数（属性权重）
# 打印每个属性的权重
# 计算总权重的和&归一化权重
# 使用Min-Max缩放对各指标进行归一化
# 添加权重，可以根据实际需求进行调整
#四象限分析中的权重通常是主观选择的，因为它们依赖于组织或分析人员的主观判断和业务需求。权重的选择取决于对不同因素的重要性和对业务目标的理解。
#但是我们都不太清楚，还是采用线性回归模型的方法得到权重

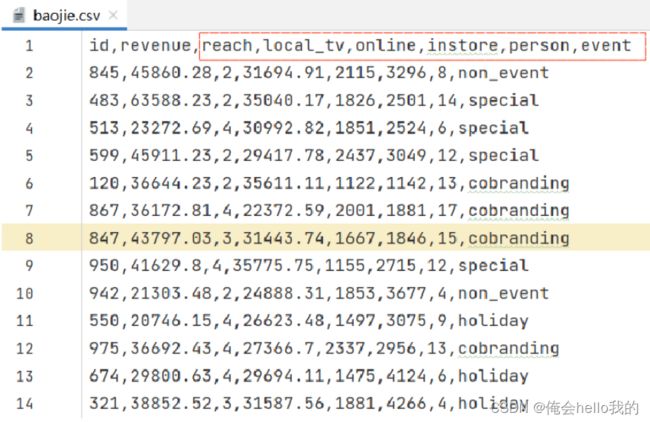
file=pd.read_csv("./baojie.csv")
event_mapping = {'non_event': 0, 'special': 0.5, 'cobranding': 0.5,'holiday':0.5}
file['event'] = file['event'].map(event_mapping)

file = file.dropna()

X = file[['reach', 'local_tv', 'online', 'instore', 'person', 'event']]
y = file['revenue']

scaler = MinMaxScaler()
X_normalized = scaler.fit_transform(X)

model = LinearRegression()
model.fit(X_normalized, y)
coefficients = model.coef_
dir={}
for i, attr in enumerate(X.columns):
    dir[attr]=coefficients[i]
total_weight = sum(dir.values())
normalized_weights = {attr: weight / total_weight for attr, weight in dir.items()}

min_max_scaler = lambda x: (x - x.min()) / (x.max() - x.min())
normalized_columns = ['reach', 'local_tv', 'online', 'instore', 'person', 'event']
file[normalized_columns] = file[normalized_columns].apply(min_max_scaler)
file["revenue"]=min_max_scaler(file["revenue"])
file.to_csv("./anaylse.csv")

weights = [x for x in normalized_weights.values()]  # 举例权重

file['investment_factor'] = file[normalized_columns].mul(weights).sum(axis=1)
re=file[['id','revenue',"investment_factor"]]
revenue_mean = re['revenue'].mean()# 计算"revenue"和"investment_factor"的平均值
investment_mean = re['investment_factor'].mean()
plt.axvline(x=revenue_mean, color='r', linestyle='--', label='Revenue Mean')
plt.axhline(y=investment_mean, color='g', linestyle='--', label='Investment Mean')
plt.figure(figsize=(8, 6))# 创建四象限图
random_sample = re.sample(n=20, random_state=1)  # 随机选择数据点设置随机种子以确保可重复性
plt.scatter(random_sample['revenue'], random_sample['investment_factor'], label='Data Points', marker='o', s=50)

for i, row in random_sample.iterrows():
    plt.text(row['revenue'], row['investment_factor'], str(row['id']))

plt.title('Four Quadrant Chart')
plt.xlabel('Revenue')
plt.ylabel('Investment Factor')
# 显示四象限图
plt.legend()
plt.grid(True)
plt.show()

数据来源：https://www.heywhale.com/mw/dataset/5f35e1ecaf3980002cb9af7a

我们想要对比投资与收益的情况，在实际管理中肯定有同样成本管理效率高使得收益高，而管理不当的肯定收益较低，我们是基于这个情况进行的分析

数据的大概情况：门店id和门店收益以及门店的各种投资成本。

我们把数据处理成id(最后得知道是那个店)，收益，成本（我们得把多种成本因素转换成一个因素）

X = file[['reach', 'local_tv', 'online', 'instore', 'person', 'event']]
y = file['revenue']

1. 数据准备与预处理:

   • 代码首先使用pandas读取了名为baojie.csv的CSV文件。
   • event列中的文本信息被映射为数值，以便进行数值分析。
   • 删除包含NaN值的行，确保数据的完整性。
   • 选择了reach, local_tv, online, instore, person, event列作为特征（自变量），revenue作为目标变量（因变量）。

2. 数据归一化:

   • 使用MinMaxScaler对特征进行归一化处理，以便在同一尺度上比较和分析不同特征。

3. 模型训练:

   这里是寻找每个成本因子的权重，因为每个成本因子对实际收益的情况我们不太好判断，就干脆使用线性回归来寻找系数

   • 使用线性回归LinearRegression模型对数据进行拟合。
   • 从模型中提取出回归系数（特征权重），这些权重用于确定每个特征对revenue的相对影响。

   model = LinearRegression()
   model.fit(X_normalized, y)
   coefficients = model.coef_ #模型训练完就有系数了
   dir={} #建立一个字典来存放系数
   for i, attr in enumerate(X.columns):
       dir[attr]=coefficients[i]
   

4. 权重处理与四象限准备:

   • 总权重被计算出来，并对每个权重进行归一化。

   • 特征值再次被归一化，并计算每个记录的“投资因子”，这是通过将归一化的特征值与归一化的权重相乘然后求和得到的。

   • total_weight = sum(dir.values())#对字典的值进行累加
     
     normalized_weights = {attr: weight / total_weight for attr, weight in dir.items()}
     #列表推导式，把系数转换为权重，权重相加为1，
     #因为之前的系数参差不齐，我们就把系数全部加一块，
     #然后挨个除以下就是我们的权重
     
     
     #处理完权重了，我们该进行数据归一化然后在与权重相乘在一一相加
     min_max_scaler = lambda x: (x - x.min()) / (x.max() - x.min())
     normalized_columns = ['reach', 'local_tv', 'online', 'instore', 'person', 'event']
     file[normalized_columns] = file[normalized_columns].apply(min_max_scaler)
     file["revenue"]=min_max_scaler(file["revenue"])
     
     
     weights = [x for x in normalized_weights.values()]  # 举例权重
     file['investment_factor'] = file[normalized_columns].mul(weights).sum(axis=1)
     

     

5. 四象限分析:

   • 根据revenue和“投资因子”的平均值，将图表分为四个象限。

   • 使用散点图展示随机选择的数据点。

   • 每个点的位置由其revenue和“投资因子”决定。

   • 图表中的红色和绿色虚线表示revenue和“投资因子”的平均值，用于界定四象限。

   • revenue_mean = re['revenue'].mean()# 计算"revenue"和"investment_factor"的平均值
     investment_mean = re['investment_factor'].mean()
     plt.axvline(x=revenue_mean, color='r', linestyle='--', label='Revenue Mean')
     plt.axhline(y=investment_mean, color='g', linestyle='--', label='Investment Mean')
     plt.figure(figsize=(8, 6))# 创建四象限图
     random_sample = re.sample(n=20, random_state=1)  # 随机选择数据点设置随机种子以确保可重复性
     plt.scatter(random_sample['revenue'], random_sample['investment_factor'], label='Data Points', marker='o', s=50)
     
     #这一步就是id的用法了，把点与id一一对应起来
     for i, row in random_sample.iterrows():
         plt.text(row['revenue'], row['investment_factor'], str(row['id']))
     
     

6. 四象限解释:

   • 第一象限（右上）: 高收益和高投资效益。
   • 第二象限（左上）: 低收益但高投资效益。
   • 第三象限（左下）: 低收益和低投资效益。
   • 第四象限（右下）: 高收益但低投资效益。

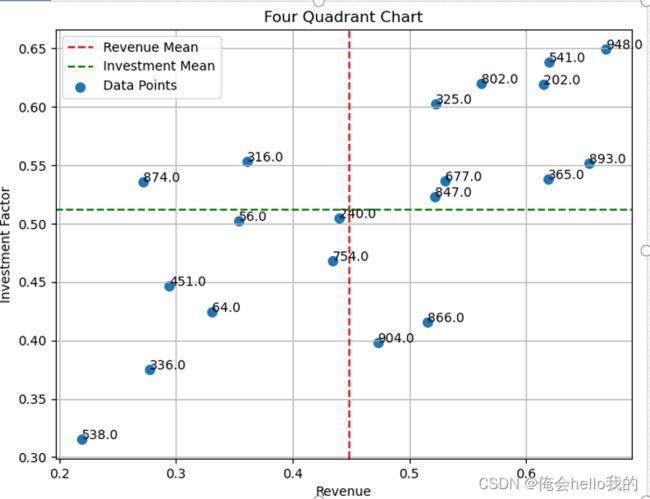
可以看到有些的投资因素是差不多的，但是收益却不同，类似的收益相同的投资却不同，我们从实际角度出发可以去调整门店管理人员的管理模式，学习好的管理方法