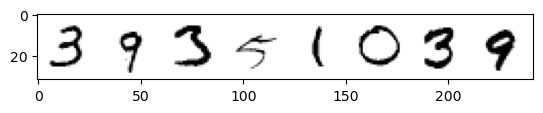扩散模型(1)代码

import torch

import torchvision

from torch import nn

from torch.utils.data import DataLoader

from diffusers import DDPMScheduler, UNet2DModel

from matplotlib import pyplot as plt

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(f'Using device: {device}')

Using device: cuda

dataset = torchvision.datasets.MNIST(root="mnist/",train=True,download=True,transform=torchvision.transforms. ToTensor())

train_dataloader = DataLoader(dataset, batch_size=8, shuffle=True)
x,y =next(iter(train_dataloader))

print('Input shape:', x.shape)

Input shape: torch.Size([8, 1, 28, 28])

print('Lable shape:', y.shape)

Lable shape: torch.Size([8])

plt.imshow(torchvision.utils.make_grid(x)[0], cmap='Greys')

扩散模型之退化过程 控制内容损坏程度，引入一个参数控制输入的“噪声量”

def corrupt(x, amount):
    # 根据amount为输入x加入噪声
    # 如果amount=0则返回输入，不做任何更改，如果amount=1那么就返回一个纯粹的噪声
    noise = torch.rand_like(x)
    amount = amount.view(-1, 1, 1, 1)
    # noisy_like = (1-amount)*x+amount*noise
    return x*(1-amount)+amount*noise

fig, axs = plt.subplots(2,1,figsize=(12,5))
axs[0].set_title('Input data')
axs[0].imshow(torchvision.utils.make_grid(x)[0], cmap='Greys')
# 加入噪声
amount = torch.linspace(0,1,x.shape[0])
noise_x = corrupt(x,amount)
axs[1].set_title('Corrupted data (----amount increases ---->)')
axs[1].imshow(torchvision.utils.make_grid(noise_x)[0], cmap='Greys')

class BasicUnet(nn.Module):
    def __init__(self, in_channels=1, out_channels=1):
        super().__init__()
        self.down_layers = torch.nn.ModuleList(
            [
             nn.Conv2d(in_channels, 32, kernel_size=5, padding=2),
             nn.Conv2d(32, 64, kernel_size=5, padding=2),
             nn.Conv2d(64, 64, kernel_size=5, padding=2),
            ]
        )
        # 下行路径
        self.up_layers = torch.nn.ModuleList(
            [

             nn.Conv2d(64, 64, kernel_size=5, padding=2),
             nn.Conv2d(64, 32, kernel_size=5, padding=2),
             nn.Conv2d(32, out_channels, kernel_size=5, padding=2),
            ]
        )
        # 上行路径
        self.act = nn.SiLU()# 激活函数
        self.downscale = nn.MaxPool2d(2)
        self.upscale = nn.Upsample(scale_factor=2)

    def forward(self, x):
        h = []
        for i, l in enumerate(self.down_layers):
            x = self.act(l(x)) # 通过运算层与激活函数
            if i < 2: # 选择下行路径的前两层
                h.append(x)  # 供残差连接使用的数据
                x = self.downscale(x) # 选择下采样适配下一层的输入

        for i, l in enumerate(self.up_layers):
            if i > 0:
                x = self.upscale(x)
                x += h.pop()
            x = self.act(l(x))

        return  x

net = BasicUnet()

x = torch.rand(8, 1, 28, 28)

net(x).shape

torch.Size([8, 1, 28, 28])

sum([p.numel() for p in net.parameters()])

309057

diffusion model有什么用-也就是说给定一个带噪声的noise_x的输入，扩散模型的输出其对原始输入x的最佳预测。

需要通过均方误差对预测值与真实值进行比较

# 流程：1、获取数据 2、添加随机噪声 3、数据输入模型 4、预测和初始图像进行比较 计算损失更新模型的参数
batch_size = 128

train_dataloader = DataLoader(dataset,batch_size=batch_size, shuffle=True)
n_epochs = 3

net = BasicUnet()
net.to(device)
# 损失函数
loss_fn = nn.MSELoss()
#优化器
opt = torch.optim.Adam(net.parameters(),lr=1e-3)
losses = []

for epoch in range(n_epochs):
    for x,y in train_dataloader:
        x = x.to(device)
        noise_amount  = torch.rand(x.shape[0]).to(device)
        noisy_x = corrupt(x,noise_amount) # 创建带噪声的NOISY_X
        # 得到模型的预测结果
        pred = net(noisy_x)

        loss = loss_fn(pred, x)

        opt.zero_grad()
        loss.backward()
        opt.step()
        # 储存损失，供后期查看
        losses.append(loss.item())

    avg_loss = sum(losses[-len(train_dataloader):])/len(train_dataloader)
    print(f'Finished epoch {epoch}. Average loss for this epoch:{avg_loss:05f}')
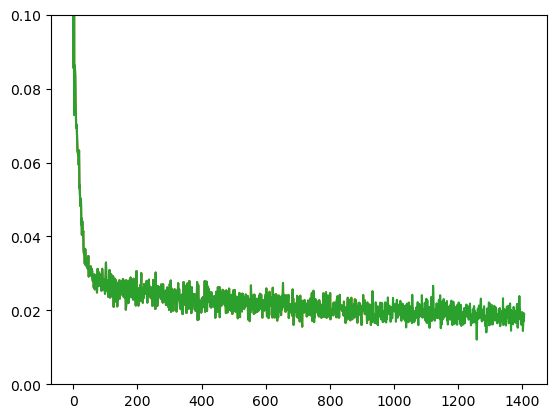
    plt.plot(losses)
    plt.ylim(0,0.1);

Finished epoch 0. Average loss for this epoch:0.027834
Finished epoch 1. Average loss for this epoch:0.021065
Finished epoch 2. Average loss for this epoch:0.019122

# 可视化模型在“带噪“输入上的表现
# 初始数据
x, y = next(iter(train_dataloader))
x = x[:8]
# 在（0-1）之间取噪声量
amount = torch.linspace(0,1, x.shape[0])
noised_x = corrupt(x, amount)
# 模型预测结果
with torch.no_grad():
    preds = net(noised_x.to(device)).detach().cpu()

# 绘图
fig,axs = plt.subplots(3, 1, figsize=(12,7))
axs[0].set_title('Input data')
axs[0].imshow(torchvision.utils.make_grid(x)[0].clip(0, 1), cmap='Greys')

axs[1].set_title('Corrupted data')
axs[1].imshow(torchvision.utils.make_grid(noised_x)[0].clip(0, 1), cmap='Greys')

axs[2].set_title('prediction data')
axs[2].imshow(torchvision.utils.make_grid(preds)[0].clip(0, 1), cmap='Greys')

采样过程

模型在高噪声量下的预测不好该怎么办呢？
从完全随机噪声开始，检测预测效果，然后朝着预测效果移动一部分，比如20%，可能新的预测效果就比上一侧的预测效果好一点，那么么就可以继续向前移动。

# 采样策略 把采样过程拆解为5步，每次只前进一步
n_steps = 5
x = torch.rand(8,1,28,28).to(device)
step_history = [x.detach().cpu()]
pred_output_history = []
for i in range(n_steps):
    with torch.no_grad():
        pred = net(x) # 预测去噪后图像
        pred_output_history.append(pred.detach().cpu()) # 保存模型

        mix_factor = 1/(n_steps - i) # 设置朝着预测方向移动多少
        x = x*(1-mix_factor)+pred*mix_factor # 移动过程
        step_history.append(x.detach().cpu()) # 记录每一次移动


fig, axs = plt.subplots(n_steps, 2, figsize=(9,4), sharex=True)
axs[0,0].set_title('x (model input)')
axs[0,1].set_title('model prediction')

for i in range(n_steps):
    axs[i,0].imshow(torchvision.utils.make_grid(step_history[i])[0].clip(0,1), cmap='Greys')
    axs[i,1].imshow(torchvision.utils.make_grid(pred_output_history[i])[0].clip(0,1), cmap='Greys')

n_steps = 20
x = torch.rand(64,1,28,28).to(device)

for i in range(n_steps):
    noise_amount = torch.ones((x.shape[0],)).to(device) * (1-(i/n_steps))# 噪声从高到低
    with torch.no_grad():
        pred = net(x)
        mix_factor = 1/(n_steps - i) # 设置朝着预测方向移动多少
        x = x*(1-mix_factor)+pred*mix_factor # 移动过程
fig, ax = plt.subplots(1, 1, figsize=(12,12))
ax.imshow(torchvision.utils.make_grid(x.detach().cpu(),nrow=8)[0].clip(0,1), cmap='Greys')

退化过程

在每个时间步都为输入图像添加少量噪声的退化过程。

如果在某个时间步给定$x_{t-1}$，就可以得到一个噪声稍微增强的$x_t$:

$$\left(x_t\mid x_{t-1}\right)=\mathcal{N}\left(x_t;\sqrt{1-{\beta }_i}{x}_{t-1},{\beta }_{t}I\right)q\left(x_1\mid x_0\right)=\prod _{t=1}^{T}q\left(x_t\mid x_{t-1}\right)$$

你可以这样理解，取$x_{t-1}$，。给它一个系数$\sqrt{1-{\beta }_t}$，然后将其与一个带有系数${\beta }_t$的噪声相加。其中，$\beta$是我们根据调度器为每个时划设定的参数，用于决定在每个时间步添加的噪声量。我们并不想通过把这个推演重复 500 次来得到，而是希望利用另一个公式，根据给出的$x_0$计算得到任意时刻$t$的$x_t$:
$$q\left(x_t\mid x_0\right)=\mathcal{N}\left(x_t;\sqrt{{\alpha }_i}{x}_0,\left(1-{\bar{\alpha }}_t\right)\mathbf{I}\right);\text{ 其中 }{\bar{\alpha }}_t=\prod ^T{\alpha }_i,{\alpha }_i=1-{\beta }_i$$