剑指offer 64. 滑动窗口的最大值
题目描述
给定一个数组和滑动窗口的大小,找出所有滑动窗口里数值的最大值。例如,如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3,那么一共存在6个滑动窗口,他们的最大值分别为{4,4,6,6,6,5}; 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个: {[2,3,4],2,6,2,5,1}, {2,[3,4,2],6,2,5,1}, {2,3,[4,2,6],2,5,1}, {2,3,4,[2,6,2],5,1}, {2,3,4,2,[6,2,5],1}, {2,3,4,2,6,[2,5,1]}。
思路:
方法一:
很容易实现,设定list窗口,后续遍历每次加入新元素到尾部,同时去掉头部元素,直接调用max(list[window])输出结果。
参考答案:
# -*- coding:utf-8 -*-
class Solution:
def maxInWindows(self, num, size):
# write code here
if not num or size > len(num) or not size:
return []
sliding_window = [num[x] for x in range(size)]
res = [max(sliding_window)]
for index in range(size, len(num)):
sliding_window.append(num[index])
sliding_window.pop(0)
res.append(max(sliding_window))
return res
进一步精简代码:
# -*- coding:utf-8 -*-
class Solution:
def maxInWindows(self, num, size):
if not num or not size: return []
_len = len(num)
res = []
for i in range(_len - size + 1):
res.append(max(num[i : i+size]))
return res
上述方案是最简单方案,时间复杂度、空间复杂度均是 O(n);下面再提供一种思路。
方法二:
我们可以使用一个双端队列deque。
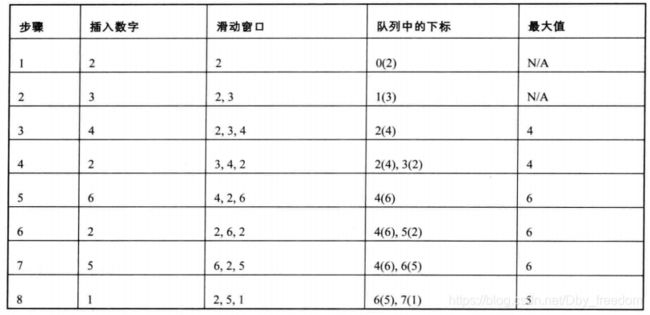
我们可以用STL中的deque来实现,接下来我们以数组{2,3,4,2,6,2,5,1}为例,来细说整体思路。
数组的第一个数字是2,把它存入队列中。第二个数字是3,比2大,所以2不可能是滑动窗口中的最大值,因此把2从队列里删除,再把3存入队列中。第三个数字是4,比3大,同样的删3存4。此时滑动窗口中已经有3个数字,而它的最大值4位于队列的头部。
第四个数字2比4小,但是当4滑出之后它还是有可能成为最大值的,所以我们把2存入队列的尾部。下一个数字是6,比4和2都大,删4和2,存6。就这样依次进行,最大值永远位于队列的头部。
但是我们怎样判断滑动窗口是否包括一个数字?应该在队列里存入数字在数组里的下标,而不是数值。当一个数字的下标与当前处理的数字的下标之差大于或者相等于滑动窗口大小时,这个数字已经从窗口中滑出,可以从队列中删除。
整体过程示意图:
C++ version:
class Solution {
public:
vector<int> maxInWindows(const vector<int>& num, unsigned int size)
{
vector<int> maxInWindows;
// 数组大小要大于等于窗口大小,并且窗口大小大于等于1
if(num.size() >= size && size >= 1){
deque<int> index;
for(unsigned int i = 0; i < size; i++){
// 如果index非空,并且新添加的数字大于等于队列中最小的数字,则删除队列中最小的数字
while(!index.empty() && num[i] >= num[index.back()]){
index.pop_back();
}
index.push_back(i);
}
for(unsigned int i = size; i < num.size(); i++){
maxInWindows.push_back(num[index.front()]);
while(!index.empty() && num[i] >= num[index.back()]){
index.pop_back();
}
// 控制窗口大小为size
if(!index.empty() && index.front() <= int(i - size)){
index.pop_front();
}
index.push_back(i);
}
maxInWindows.push_back(num[index.front()]);
}
return maxInWindows;
}
};
Python version:
# -*- coding:utf-8 -*-
class Solution:
def maxInWindows(self, num, size):
# write code here
if not num or size <=0:
return []
res = []
if len(num) >= size:
index = []
for i in range(size):
while len(index) > 0 and num[i] > num[index[-1]]:
index.pop()
index.append(i)
for i in range(size, len(num)):
res.append(num[index[0]])
while len(index) > 0 and num[i] >= num[index[-1]]:
index.pop()
if len(index) > 0 and index[0] <= i - size:
index.pop(0)
index.append(i)
res.append(num[index[0]])
return res
Note
- 一直想尝试直接将时间复杂度降到 O(n),最后调用了max函数实现,姑且算是完成目标吧。
- 第二种方法虽然更繁琐一些,但是其思路很到位,空间复杂度更低;