因果推断《Causal Inference in Python》中文笔记第8章 双重差分
《Causal Inference in Python: Applying Causal Inference in the Tech Industry》因果推断啃书系列
第1章 因果推断导论
第2章 随机实验与统计学回顾
第3章 图形化因果模型
第4章 线性回归的不合理有效性
第5章 倾向分
第6章 效果异质性
第7章 元学习器
第8章 双重差分
持续更新中:
第9章 综合控制
第10章 Geo实验与Switchback实验
第11章 不依从性与工具
第12章 后续行动
《Causal Inference in Python》第8章 双重差分
- 第8章 双重差分
-
- 8.1 面板数据(Panel Data)
- 8.2 典型双重差分(Canonical Difference-in-Differences)
-
- 8.2.1 带有结果增长的双重差分法
- 8.2.2 带有OLS的双重差分法
- 8.2.3 带有固定效应(Fixed Effects)的双重差分法
- 8.2.4 多时段
- 8.2.5 推理
- 8.3 识别假设
-
- 8.3.1 平行趋势(Parallel Trends)
- 8.3.2 无预期假设(No Anticipation Assumption)与SUTVA
- 8.3.3 严格外生性(Strict Exogeneity)
- 8.3.4 无时间变化混淆因子(No Time Varying Confounders)
- 8.3.5 无反馈(No Feedback)
- 8.3.6 无延续效应(No Carryover)因变量和无滞后(no Lagged)因变量
- 8.4 效果时间动力学(Effect Dynamics Over Time)
- 8.5 带有协变量的双重差分法(Diff-in-Diff with Covariates)
- 8.6 双重鲁棒性双重差分法(Doubly Robust Diff-in-Diff)
-
- 8.6.1 倾向得分模型
- 8.6.2 结果增量模型(Delta Outcome Model)
- 8.6.3 整合所有步骤
- 8.7 交错采纳设计(Staggered Adoption)
-
- 8.7.1 时间上的效果异质性(Heterogeneous Effect over Time)
- 8.7.2 协变量(Covariates)
- 8.8 要点总结
第8章 双重差分
在讨论完干预效果的异质性之后,是时候稍微转换一下话题,回到平均干预效果上来了。在接下来的几章中,你将学习如何利用面板数据(Panel Data, 或称平行数据)进行因果推断。
面板数据是一种数据结构,它在时间上具有重复观测值。由于你在多个时间段对相同的单元进行观测,因此你可以看到相同单元在干预之前和之后的情况。这使得面板数据成为在随机化不可行时识别因果效应的一个有前途的替代方法。当你拥有观测数据(非随机化)和可能存在未观测到的混淆因子时,面板数据方法在正确识别干预效果上非常有效。
在本章中,你将了解为什么面板数据在因果推断方面如此有趣。然后,你将学习面板数据最著名的因果推断估算器:双重差分,以及其多种变体。为了保持趣味性,你将在弄清楚线下营销活动的效果的背景下进行所有这些学习。
数据类型(Data Regimes)
与面板数据或纵向设计(Longitudinal Design)相比,横截面数据(Cross-sectional Data)的特点是每个单元只出现一次。介于两者之间的第三类被称为重复横截面数据(Repeated Cross-sectional Data)。这类数据涉及多个时间条目,但每个条目中的单元不一定相同。到目前为止,你处理的数据包括同一单元随时间的重复观测值(例如,当试图确定折扣对餐厅销售的影响时),但为了简单起见,我们将该数据视为横截面数据。这有时被称为合并横截面数据(Pooled Cross-section Data)。
8.1 面板数据(Panel Data)
为了激发面板数据的使用热情,我将主要谈论因果推断在市场营销中的应用。市场营销特别有趣,因为在进行随机实验时存在众所周知的困难。在市场营销中,你往往无法控制谁接受到干预,也就是无法控制谁看到了你的广告。当一个新用户来到你的网站或下载你的应用时,你没有办法知道这个用户是因为看到了你的广告活动还是其他原因而来的。即使你知道客户点击了你的营销链接,也很难说他们是不是原本就会使用你的产品。例如,如果客户真的在寻找你的产品,他点击了你的谷歌赞助链接,他们也可能只是向下滚动一点去点击非赞助链接,点击了赞助链接可能仅仅是因为先看到了。
这个问题在离线营销中甚至更显著。你怎么知道在城市里放置一些广告牌带来的价值超过其成本呢?因此,市场营销中的一种常见做法是进行地理实验(Geo-experiments):你可以在一些地理区域部署营销活动,但不在其他地区部署,然后进行比较。在这种设计中,面板数据方法特别有趣:你可以在多个时间段内收集整个地理区域(单元)的数据。
正如我所说,面板数据是指你在多个时间周期 t t t 内对多个单元 i i i 进行观测的数据。在一些电商网站上,单元可能是人,时间周期 t t t 可能是天或月。但单元并不一定非得是单一客户。例如,在线下营销活动的背景下, i i i 可以是你放置产品广告牌的城市。
因此,为了更具体地说明,以下数据框mkt_data以面板格式呈现了营销数据。每一行都是一个(日期,城市)组合:
from toolz import *
import pandas as pd
import numpy as np
import statsmodels.formula.api as smf
import seaborn as sns
from matplotlib import pyplot as plt
import matplotlib
from cycler import cycler
color=['0.0', '0.4', '0.8']
default_cycler = (cycler(color=color))
linestyle=['-', '--', ':', '-.']
marker=['o', 'v', 'd', 'p']
plt.rc('axes', prop_cycle=default_cycler)
import pandas as pd
import numpy as np
mkt_data = (pd.read_csv("./data/short_offline_mkt_south.csv")
.astype({"date":"datetime64[ns]"}))
mkt_data.head()
| date | city | region | treated | tau | downloads | post | |
|---|---|---|---|---|---|---|---|
| 0 | 2021-05-01 | 5 | S | 0 | 0 | 51 | 0 |
| 1 | 2021-05-02 | 5 | S | 0 | 0 | 51 | 0 |
| 2 | 2021-05-03 | 5 | S | 0 | 0 | 51 | 0 |
| 3 | 2021-05-04 | 5 | S | 0 | 0 | 50 | 0 |
| 4 | 2021-05-05 | 5 | S | 0 | 0 | 49 | 0 |
这个数据框按照日期和城市进行了排序。你关心的结果变量是下载次数。由于 t t t 将用于表示时间,为了避免混淆,从现在开始,我将使用 D D D 来表示干预。此外,在面板数据的文献中,干预经常被称为介入(intervention)。我将交替使用这两个术语。在这个例子中,营销团队在 D i = 1 D_i=1 Di=1 的城市进行了线下活动。至于时间维度,让我们确定 T T T 为周期数, T p r e T_{pre} Tpre 为干预前的周期。你可以将时间向量视为 t = 1 , 2 , . . . , T p r e , T p r e + 1 , . . . , T t={1,2,...,Tpre,Tpre+1,...,T} t=1,2,...,Tpre,Tpre+1,...,T。 T p r e , . . . , T T_{pre},...,T Tpre,...,T,被称为干预后周期(Post Intervention)。为了简化符号,我经常使用 P o s t Post Post 虚拟变量,当 t > T p r e t>Tpre t>Tpre 时为1,否则为0。
干预只发生在干预后的时期,对干预单元 D = 1 D=1 D=1 在 t > T p r e t>T_{pre} t>Tpre 时进行。干预和干预后的组合将表示为 W = D ∗ 1 ( t > T p r e ) W=D*1(t>T_{pre}) W=D∗1(t>Tpre) 或 W = D ∗ P o s t W=D*Post W=D∗Post。以下是营销数据中这种情况的一个例子:
(mkt_data
.assign(w = lambda d: d["treated"]*d["post"])
.groupby(["w"])
.agg({"date":[min, max]}))
| date | ||
|---|---|---|
| min | max | |
| w | ||
| 0 | 2021-05-01 | 2021-06-01 |
| 1 | 2021-05-15 | 2021-06-01 |
你可以看到,干预前的周期是从2021年5月1日到2021年5月15日,而干预后的周期是从2021年5月15日到2021年6月1日。
这个数据集也有一个 τ \tau τ 变量来表示干预效果。由于这些数据是模拟的,我清楚地知道这个效果是什么。我在这个数据集中包含它只是为了让你检查你将学习的方法是否能很好地识别因果效应。但不要习惯有它,在现实生活中,你不会有这种奢侈的指导。
现在你对数据有了更好的理解,并学习了一些新的技术符号,你可以更准确地重述你的目标。你想了解干预活动发生后,线下市场营销活动对那些受到干预的城市的效果:
A T T = E ( Y i t ( 1 ) − Y i t ( 0 ) ∣ D = 1 , t > T p r e ) ATT=E(Y_{it}(1)-Y_{it}(0)|D=1,t>T_{pre}) ATT=E(Yit(1)−Yit(0)∣D=1,t>Tpre)
这是ATT(平均干预效果),因为你只关注了解干预活动对 D = 1 D=1 D=1 的城市在干预活动启动后 t > T p r e t>T_{pre} t>Tpre 的影响。由于 Y i t ( 1 ) Y_{it}(1) Yit(1) 是可观测的,你可以通过填补缺失的潜在结果 E ( Y ( 0 ) ∣ D = 1. P o s t = 1 ) E(Y(0)|D=1.Post=1) E(Y(0)∣D=1.Post=1) 来实现这一目标。
下图展示了当面板数据以单元-时间矩阵形式表示观测结果时,为何会变得特别有趣。这个矩阵突出了这样一个事实,即 Y ( 1 ) Y(1) Y(1) 只在干预后的周期内对于受干预单元是可观察的,而对于所有其他单元,你只能观察到 Y ( 0 ) Y(0) Y(0)。尽管如此,这些单元仍然可以用于估算缺失的潜在结果 E ( Y ( 0 ) ∣ D = 1 , t > T p r e ) E(Y(0)|D=1,t>T_{pre}) E(Y(0)∣D=1,t>Tpre)。你可以通过对照单元在干预后期间的结果来利用单元之间的相关性,并且你还可以通过在干预前周期利用受干预单元的结果来利用时间上的相关性。
这张图也展示了为什么在面板数据的大多数应用中,你应该关注ATT:对于受干预的单元,填补 Y ( 0 ) Y(0) Y(0) 要容易得多。如果你想要的是ATC(对照组的平均效果),你就必须填补 Y ( 1 ) Y(1) Y(1)。然而,上图中只有右上角的单元格是可以观察到这种潜在结果的。
现在你已经对面板数据有了简单的了解,是时候探索一些利用它来识别和估算干预效果的机制了。
8.2 典型双重差分(Canonical Difference-in-Differences)
双重差分的基本思想是通过利用干预组的基线,并应用对照组的结果变化(增长)来估算缺失的潜在结果 E ( Y ( 0 ) ∣ D = 1 , P o s t = 1 ) E(Y(0)|D=1,Post=1) E(Y(0)∣D=1,Post=1):
E ( Y ( 0 ) ∣ D = 1 , P o s t = 1 ) = E ( Y ∣ D = 1 , P o s t = 0 ) + ( E ( Y ∣ D = 0 , P o s t = 1 ) − E ( Y ∣ D = 0 , P o s t = 0 ) ) \begin{aligned} E(Y(0)|D=1,Post=1) &= E(Y|D=1,Post=0) \\ &+ (E(Y|D=0,Post=1) -E(Y|D=0,Post=0)) \end{aligned} E(Y(0)∣D=1,Post=1)=E(Y∣D=1,Post=0)+(E(Y∣D=0,Post=1)−E(Y∣D=0,Post=0))
其中,你可以通过用样本平均值替换右侧的期望值来估算 E ( Y ( 0 ) ∣ D = 1 , P o s t = 1 ) E(Y(0)|D=1,Post=1) E(Y(0)∣D=1,Post=1)。这种方法被称为双重差分(DID)估算器,因为如果在ATT中将前述表达式替换为 E ( Y ( 0 ) ∣ D = 1 , P o s t = 1 ) E(Y(0)|D=1,Post=1) E(Y(0)∣D=1,Post=1),你得到的正是差分中的差分:
A T T = ( E ( Y ∣ D = 1 , P o s t = 1 ) − E ( Y ∣ D = 1 , P o s t = 0 ) ) − ( E ( Y ∣ D = 0 , P o s t = 1 ) − E ( Y ∣ D = 0 , P o s t = 0 ) ) \begin{aligned} ATT &= (E(Y|D=1,Post=1) -E(Y|D=1,Post=0)) \\ &- (E(Y|D=0,Post=1) -E(Y|D=0,Post=0)) \end{aligned} ATT=(E(Y∣D=1,Post=1)−E(Y∣D=1,Post=0))−(E(Y∣D=0,Post=1)−E(Y∣D=0,Post=0))
不要被这些期望值吓到。在其典型形式中,你可以很容易地得到DID估算。首先,将数据的时间段分为干预前和干预后。然后,将单元分为干预组和对照组。最后,你可以简单地计算所有四个单元格的平均值:干预前对照组、干预前干预组、干预后对照组以及干预后干预组:
did_data = (mkt_data
.groupby(["treated", "post"])
.agg({"downloads":"mean", "date": "min"}))
did_data
| downloads | date | ||
|---|---|---|---|
| treated | post | ||
| 0 | 0 | 50.335034 | 2021-05-01 |
| 0 | 1 | 50.556878 | 2021-05-15 |
| 1 | 0 | 50.944444 | 2021-05-01 |
| 1 | 1 | 51.858025 | 2021-05-15 |
以上是获取DID估算所需的所有数据。对于干预基线 E ( Y ∣ D = 1 , P o s t = 0 ) E(Y|D=1,Post=0) E(Y∣D=1,Post=0),您可以使用did_data.loc[1]索引到干预组,然后使用后续的.loc[0]索引到干预前周期。为了获得对照组结果的变化 E ( Y ∣ D = 0 , P o s t = 1 ) − E ( Y ∣ D = 0 , P o s t = 0 ) E(Y|D=0,Post=1) -E(Y|D=0,Post=0) E(Y∣D=0,Post=1)−E(Y∣D=0,Post=0),可以使用did_data.loc[0]索引到对照组,使用.diff()计算差值,并使用后续的.loc[1]索引到最后一行。将对照趋势添加到干预基线中,可以估算出反事实 E ( Y ( 0 ) ∣ D = 1 , P o s t = 1 ) E(Y(0)|D=1,Post=1) E(Y(0)∣D=1,Post=1)。为了获得ATT,可以从干预后周期的干预平均结果中减去该估算值:
y0_est = (did_data.loc[1].loc[0, "downloads"] # treated baseline
# control evolution
+ did_data.loc[0].diff().loc[1, "downloads"])
att = did_data.loc[1].loc[1, "downloads"] - y0_est
att
0.6917359536407233
如果将这个数值与真实的ATT(筛选干预单元和干预后周期)进行比较,你会发现DID估算值非常接近其试图估算的值:
mkt_data.query("post==1").query("treated==1")["tau"].mean()
0.7660316402518457
最低工资与就业
在90年代,大卫·卡德(David Card)和艾伦·克鲁格(Alan Krueger)使用2×2双重差分法来挑战传统经济理论,该理论认为最低工资上涨会导致就业减少。他们观察了新泽西州和宾夕法尼亚州快餐店的数据,对比了新泽西州最低工资增长之前和之后的情形。研究发现,没有证据表明最低工资增长导致就业减少。这篇论文具有极大的影响力,被多次回顾和研究,其结果被证明是非常可靠的。最终,由于其影响力以及有助于推广双重差分法,卡德在2021年被授予诺贝尔奖。
8.2.1 带有结果增长的双重差分法
关于双重差分法的另一种非常有趣的观点是,意识到该方法在时间维度上对数据进行了分化。让我们定义单元 i i i 在时间上的结果差异为 Δ y i = E ( y i ∣ t > T p r e ) − E ( y i ∣ t ≤ T p r e ) \Delta y_i=E(y_i|t>T_{pre}) -E(y_i|t≤T_{pre}) Δyi=E(yi∣t>Tpre)−E(yi∣t≤Tpre)。现在,让我们将原始数据(按时间和单元划分)转换为一个数据框,其中包含 Δ y i \Delta y_i Δyi,时间维度已经被分化出来:
pre = mkt_data.query("post==0").groupby("city")["downloads"].mean()
post = mkt_data.query("post==1").groupby("city")["downloads"].mean()
delta_y = ((post - pre)
.rename("delta_y")
.to_frame()
# add the treatment dummy
.join(mkt_data.groupby("city")["treated"].max()))
delta_y.tail()
| delta_y | treated | |
|---|---|---|
| city | ||
| 192 | 0.555556 | 0 |
| 193 | 0.166667 | 0 |
| 195 | 0.420635 | 0 |
| 196 | 0.119048 | 0 |
| 197 | 1.595238 | 1 |
接下来,可以使用潜在结果符号来定义 Δ y \Delta y Δy 的ATT:
A T T = E ( Δ y 1 − Δ y 0 ) ATT=E(\Delta y_1 -\Delta y_0) ATT=E(Δy1−Δy0)
双重差分法试图通过用对照单元的平均值替换 Δ y 0 \Delta y_0 Δy0 来确定ATT:
A T T = E ( Δ y ∣ D = 1 ) − E ( Δ y ∣ D = 0 ) ATT=E(\Delta y|D=1) -E(\Delta y|D=0) ATT=E(Δy∣D=1)−E(Δy∣D=0)
如果用样本平均值替换这些期望,你会发现得到与之前相同的双重差分估算值:
(delta_y.query("treated==1")["delta_y"].mean()
- delta_y.query("treated==0")["delta_y"].mean())
0.6917359536407155
这是对双重差分法(DID)一种有趣的理解,因为它非常清晰地指出了其假设,即 E ( Δ y 0 ) = E ( Δ y ∣ D = 0 ) E(\Delta y_0)=E(\Delta y|D=0) E(Δy0)=E(Δy∣D=0),我们稍后会详细讨论这一点。
由于这些内容技术性很强且涉及大量数学知识,我想通过绘制干预组和对照组的观测结果随时间变化的情况,以及干预单元的反事实估算结果,让你更直观地理解DID。在下图中, E ( Y ( 0 ) ∣ D = 1 ) E(Y(0)|D=1) E(Y(0)∣D=1) 的DID估算以虚线表示,它是通过将对照组的轨迹应用于干预基线而得到的。然后,估算的平均干预效果(ATT)将是反事实估算结果 Y ( 0 ) Y(0) Y(0) 与观测结果 Y ( 1 ) Y(1) Y(1) 之间的差异,两者都在干预后周期(dot和cross之间的差异):
did_plt = did_data.reset_index()
plt.figure(figsize=(10,4))
sns.scatterplot(data=did_plt.query("treated==0"), x="date", y="downloads", s=100, color="C0", marker="s")
sns.lineplot(data=did_plt.query("treated==0"), x="date", y="downloads", label="Control", color="C0")
sns.scatterplot(data=did_plt.query("treated==1"), x="date", y="downloads", s=100, color="C1", marker="x")
sns.lineplot(data=did_plt.query("treated==1"), x="date", y="downloads", label="Treated", color="C1",)
plt.plot(did_data.loc[1, "date"], [did_data.loc[1, "downloads"][0], y0_est], color="C2", linestyle="dashed", label="Y(0)|D=1")
plt.scatter(did_data.loc[1, "date"], [did_data.loc[1, "downloads"][0], y0_est], color="C2", s=50)
plt.xticks(rotation = 45);
plt.legend()
8.2.2 带有OLS的双重差分法
尽管可以通过手动计算平均值或取差值来实现双重差分法(DID),但如果这一章没有包含相当多的线性回归,那么它就称不上是一章体面的因果推断。不出所料,使用饱和回归模型可以得到完全相同的DID估计值。首先,让我们根据城市和周期(干预前和干预后)对你的每日数据进行分组。然后,对于每个城市和周期的组合,你可以得到每日平均下载量。此外,我也要获取每个周期的开始日期以及每个城市的干预状态。开始日期在估算器中并未使用,但有助于理解干预的时间点:
did_data = (mkt_data
.groupby(["city", "post"])
.agg({"downloads":"mean", "date": "min", "treated": "max"})
.reset_index())
did_data.head()
| city | post | downloads | date | treated | |
|---|---|---|---|---|---|
| 0 | 5 | 0 | 50.642857 | 2021-05-01 | 0 |
| 1 | 5 | 1 | 50.166667 | 2021-05-15 | 0 |
| 2 | 15 | 0 | 49.142857 | 2021-05-01 | 0 |
| 3 | 15 | 1 | 49.166667 | 2021-05-15 | 0 |
| 4 | 20 | 0 | 48.785714 | 2021-05-01 | 0 |
使用这个城市的周期数据集,你可以估算以下线性模型:
Y i t = β 0 + β 1 D i + β 2 P o s t t + β 3 D i P o s t t + e i t Y_{it}=\beta_0 +\beta_1 D_i +\beta_2 Post_t +\beta_3 D_i Post_t +e_{it} Yit=β0+β1Di+β2Postt+β3DiPostt+eit
参数估算值 β ^ 3 \widehat \beta_3 β 3 就是双重差分估算值(DID estimate)。为了理解为什么是这样,请注意 β 0 \beta_0 β0 是对照组的基线,在这种情况下, β 0 \beta_0 β0 是对照城市在 2021 年 5 月 15 日之前的下载水平。如果你打开干预城市虚拟变量,你将得到 β 0 + β 1 \beta_0+\beta_1 β0+β1。因此, β 0 + β 1 \beta_0+\beta_1 β0+β1 是干预城市在干预之前的基线。 β 1 \beta_1 β1 表示干预城市和对照城市之间的基线差异。如果你关闭干预虚拟变量并打开干预后的虚拟变量,你将得到 β 0 + β 2 \beta_0+\beta_2 β0+β2,这是在干预之后对照城市的水平。因此, β 2 \beta_2 β2 是对照组的趋势,它表示对照组在干预之前到之后的增长量。
回顾一下, β 1 \beta_1 β1 是从对照组到干预组的增量, β 2 \beta_2 β2 是从干预前到干预后的增量。最后,如果你同时打开干预过的和干预后的虚拟变量,你将得到 β 0 + β 1 + β 2 + β 3 \beta_0+\beta_1+\beta_2+\beta_3 β0+β1+β2+β3。这是干预后干预城市的水平,这意味着 β 3 \beta_3 β3 是从干预城市到对照城市以及从干预前到干预后结果的增量。换句话说,它就是双重差分估算值:
import statsmodels.formula.api as smf
smf.ols(
'downloads ~ treated*post', data=did_data
).fit().params["treated:post"]
0.6917359536406904
8.2.3 带有固定效应(Fixed Effects)的双重差分法
理解双重差分法(DID)的另一种方式是通过时间和单元固定效应模型(双向固定效应或TWFE)。在这个模型中,你有干预效果 τ \tau τ,单元和时间固定效应分别为 α i \alpha_i αi 和 γ t \gamma_t γt:
Y i t = τ W i t + α i + γ t + e i t Y_{it}=\tau W_{it} +\alpha_i +\gamma_t +e_{it} Yit=τWit+αi+γt+eit
为了简化表述,这里我使用 W i t = D i P o s t t W_{it}=D_i Post_t Wit=DiPostt。
如果对这个模型进行估算,与 W W W 相关的参数估算值将匹配之前得到的DID估算值,并恢复ATT。要做到这一点,回忆第4章的内容,你可以通过使用虚拟变量或通过去均值化数据来估算固定效应。这里,为了简单起见,我们仅使用虚拟变量的方法。也就是说,我们包含城市和周期虚拟变量,用C(city)和C(post)表示。此外,你需要通过乘以干预的和干预后的虚拟变量来创建 W W W。只需记住,*运算符创建两项之间的交互以及它们自身的项。因为你只想要交互,所以需要:运算符:
m = smf.ols('downloads ~ treated:post + C(city) + C(post)',
data=did_data).fit()
m.params["treated:post"]
0.6917359536407091
再一次,你得到了完全相同的参数估算。
8.2.4 多时段
典型的双重差分设置要求你只有四个数据单元格:干预前和干预后,干预组和对照组。但它并不要求将干预前和干预后的时间段聚合到一个单一的块中。典型的双重差分只要求你有一个所谓的块设计:一组从未被干预的单元和一组在同一时间段内最终被干预的单元。也就是说,你不能让干预在不同的时刻推广到不同的单元(你很快就会学到这一点)。你正在处理的营销示例正好符合这种格式,这意味着你不需要将其聚合到干预前和干预后的时间段。你可以直接使用它。
你可以在下图中可视化这个块设计,它绘制了每个城市随时间的处理分配情况。它还显示了结果随时间的演变,这样你可以更好地感受双重差分的含义。即,它试图观察在干预措施发生后,处理组和对照组之间的差异是否增加:
import matplotlib.ticker as plticker
fig, (ax1, ax2) = plt.subplots(2,1, figsize=(9, 12), sharex=True)
heat_plt = (mkt_data
.assign(treated=lambda d: d.groupby("city")["treated"].transform(max))
.astype({"date":"str"})
.assign(treated=mkt_data["treated"]*mkt_data["post"])
.pivot("city", "date", "treated")
.reset_index()
.sort_values(max(mkt_data["date"].astype(str)), ascending=False)
.reset_index()
.drop(columns=["city"])
.rename(columns={"index":"city"})
.set_index("city"))
sns.heatmap(heat_plt, cmap="gray", linewidths=0.01, linecolor="0.5", ax=ax1, cbar=False)
ax1.set_title("Treatment Assignment")
sns.lineplot(data=mkt_data.astype({"date":"str"}),
x="date", y="downloads", hue="treated", ax=ax2)
loc = plticker.MultipleLocator(base=2.0)
# ax2.xaxis.set_major_locator(loc)
ax2.vlines("2021-05-15", mkt_data["downloads"].min(), mkt_data["downloads"].max(), color="black", ls="dashed", label="Interv.")
ax2.set_title("Outcome Over Time")
plt.xticks(rotation = 50);
要获得这些分类数据的DID估算值,你可以使用与之前完全相同的公式。也就是说,你可以归在干预组、干预后虚拟变量以及它们的交互项上对结果进行回归:
m = smf.ols('downloads ~ treated*post', data=mkt_data).fit()
m.params["treated:post"]
0.6917359536407226
或者,你也可以使用固定效应规范:
m = smf.ols('downloads ~ treated:post + C(city) + C(date)',
data=mkt_data).fit()
m.params["treated:post"]
0.6917359536407017
我刚刚展示了获得相同DID估算值的不同方法。通过这样做,我希望你能从所有这些方法中汇聚见解,增加对正在发生的事情的理解。但如果你仔细观察会发现,我故意隐藏了刚刚运行的回归的置信区间,是因为这些回归的置信区间可能是错误的。
8.2.5 推理
置信区间可能是错误的,因为老实说,使用面板数据进行推断是非常棘手的。最近有很多关于这个话题的研究,这当然很好,但也突出了面板数据是一个我们仍在研究如何处理的领域。这里的问题是,你有 N ⋅ T N·T N⋅T 个数据点,但它们不是独立且同分布的,因为同一个单元会出现多次。事实上,干预是分配给单元的,而不是分配给时间段的,所以你可以认为你的样本大小实际上只是 N N N,而不是 N ⋅ T N·T N⋅T,尽管你的回归在计算标准误差时会考虑后者。
要纠正回归中过于乐观的标准误差,你可以按单元(例如,城市)对标准误差进行聚类:
m = smf.ols(
'downloads ~ treated:post + C(city) + C(date)', data=mkt_data
).fit(cov_type='cluster', cov_kwds={'groups': mkt_data['city']})
print("ATT:", m.params["treated:post"])
m.conf_int().loc["treated:post"]
ATT: 0.6917359536407017
0 0.296101
1 1.087370
Name: treated:post, dtype: float64
上面对误差进行聚类得到的置信区间,比不进行聚类的置信区间更宽:
m = smf.ols('downloads ~ treated:post + C(city) + C(date)',
data=mkt_data).fit()
print("ATT:", m.params["treated:post"])
m.conf_int().loc["treated:post"]
ATT: 0.6917359536407017
0 0.478014
1 0.905457
Name: treated:post, dtype: float64
此外,请看你将每日数据框mkt_data替换为按单元和干预前后周期汇总的数据框时会发生什么:
m = smf.ols(
'downloads ~ treated:post + C(city) + C(date)', data=did_data
).fit(cov_type='cluster', cov_kwds={'groups': did_data['city']})
print("ATT:", m.params["treated:post"])
m.conf_int().loc["treated:post"]
ATT: 0.6917359536407091
0 0.138188
1 1.245284
Name: treated:post, dtype: float64
置信区间变得更宽了!这恰恰表明,尽管样本大小应该来源于单元而非时间段,但每个单元的周期越多,越可以减少方差。
正如你在本章后面将看到的,一些非典型的双重差分方法并没有计算置信区间的标准方法。在那些情况下,你可以选择对整个估算过程进行自助法(bootstrap,在第5章有介绍),你只需要在这里小心一点。由于你有重复的单元,同一单元的模型误差是相关的。因此,你需要抽样(有放回)整个单元。这个过程叫做块自助法(block bootstrap)。要实现它,你首先需要写一个函数,用于对单元进行有放回抽样:
def block_sample(df, unit_col):
units = df[unit_col].unique()
sample = np.random.choice(units, size=len(units), replace=True)
return (df
.set_index(unit_col)
.loc[sample]
.reset_index(level=[unit_col]))
一旦你有了这个函数,你就可以调整第5章中的自助法代码来实现块自助法:
from joblib import Parallel, delayed
def block_bootstrap(data, est_fn, unit_col,
rounds=200, seed=123, pcts=[2.5, 97.5]):
np.random.seed(seed)
stats = Parallel(n_jobs=4)(
delayed(est_fn)(block_sample(data, unit_col=unit_col))
for _ in range(rounds))
return np.percentile(stats, pcts)
最后,为了检查一切是否按预期工作,你可以使用这个函数来计算营销数据的DID估算器的95%置信区间。得到的置信区间与你之前标准误差按单元聚类得到的很相似。这是一个很好的指标,表明你的块自助法函数正在正常工作。
def est_fn(df):
m = smf.ols('downloads ~ treated:post + C(city) + C(date)',
data=df).fit()
return m.params["treated:post"]
block_bootstrap(mkt_data, est_fn, "city")
array([0.23162214, 1.14002646])
在结束这一部分之前,我想提醒你的是,尽管块自助法非常方便,但也存在一些问题。例如,如果干预单元的数量很少,你可能会抽样到一个没有干预单元的样本。再次强调,面板数据的推理是一个复杂的话题,我们还没有一个明确的答案。
另请参阅
如果你想了解更多,可以查看Abadie、Athey、Imbens和Wooldridge四位因果推断领域的杰出研究者2022年9月的论文《何时应调整标准误差以进行聚类》(When Should You Adjust Standard Errors for Clustering)。我还建议你查阅一些替代的推理方法,如Victor Chernozhukov等人的论文《用于反事实和合成控制的精确且稳健的保真推理方法》(An Exact and Robust Conformal Inference Method for Counterfactual and Synthetic Controls)中概述的方法。
8.3 识别假设
正如你现在可能知道的,因果推断是统计工具与假设之间的持续交互。在这一章中,我选择了从统计工具开始,展示双重差分如何利用单元和时间关系来估算干预效果,还给了你一个具体的例子来理解。现在,是时候更深入地挖掘在使用双重差分时所做的假设是哪种,有时你甚至没有意识到你做了假设。
8.3.1 平行趋势(Parallel Trends)
在这本书的前面部分,当使用横截面(Cross-sectional)数据时,一个关键的识别假设是干预与潜在结果是独立的,取决于观察到的协变量。双重差分做了一个类似但更弱的假设:平行趋势(Parallel Trends)。
如果你仔细思考,双重差分估算器在利用时间和单元相关性方面进行因果推断是非常直观的。如果你只有单元(没有时间维度),你将不得不使用对照组来估算干预组的 Y ( 0 ) Y(0) Y(0)。另一方面,如果你有时间维度,但没有对照组(所有单元在某个时间点都受到了干预),你将不得不使用干预组过去的 Y ( 0 ) Y(0) Y(0) 进行一种前后比较。这两种方法都需要相当强的假设。你要么假设对照组的结果可以识别 E ( Y ( 0 ) ∣ D = 1 , P o s t = 1 ) E(Y(0)|D=1,Post=1) E(Y(0)∣D=1,Post=1),这只有在干预组和对照组可比(如在随机对照试验中)的情况下才成立,要么假设干预组的结果在时间上是一条直线,在这种情况下,你可以使用干预组过去的结果来识别 E ( Y ( 0 ) ∣ D = 1 , P o s t = 1 ) E(Y(0)|D=1,Post=1) E(Y(0)∣D=1,Post=1)。相比之下,双重差分做出了一个较弱的假设:在没有干预的情况下,干预组和对照组的结果轨迹在时间上的平均值是相同的。它假设 Y ( 0 ) Y(0) Y(0) 的趋势是平行的:
E ( Y ( 0 ) i t = 1 − Y ( 0 ) i t = 0 ∣ D = 1 ) = E ( Y ( 0 ) i t = 1 − Y ( 0 ) i t = 0 ∣ D = 0 ) E(Y(0)_{it=1} -Y(0)_{it=0}|D=1) = E(Y(0)_{it=1} -Y(0)_{it=0}|D=0) E(Y(0)it=1−Y(0)it=0∣D=1)=E(Y(0)it=1−Y(0)it=0∣D=0)
这个假设是不可检验的,因为它包含了一个不可观测的项: E ( Y ( 0 ) i t = 1 ∣ D = 1 ) E(Y(0)_{it=1}|D=1) E(Y(0)it=1∣D=1)。然而,为了理解它,我们暂时假设可以观测到所有时间段的 Y ( 0 ) Y(0) Y(0) 的潜在结果。在下面的图表中,我用虚线来表示它们。这里你可以看到干预组和对照组在四个时间段的潜在结果 Y ( 0 ) Y(0) Y(0)。此外,每个图有四个点,代表干预组和对照组的观测数据,以及对照组的干预DID估算轨迹,用虚线表示。这条虚线和干预组的干预后结果之间的差异是ATT的DID估算。
然而,真正的ATT是干预组的干预后结果与灰色虚线之间的差异,灰色虚线代表干预组的未观测到的 Y ( 0 ) Y(0) Y(0):
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(20,7))
obs_df = pd.DataFrame(dict(
period = [2,3, 2,3],
treated = [0,0, 1,1],
y = [4,6, 10,16],
))
baseline = 10-4
plt_d1 = pd.DataFrame(dict(
period = [1,2,3,4, 1,2,3,4],
treated = [0,0,0,0, 1,1,1,1],
y = [2,4,6,8, 8,10,12,14],
))
sns.lineplot(data=plt_d1, x="period", y="y", hue="treated", linestyle="dashed", legend=None, ax=ax1)
sns.lineplot(data=obs_df, x="period", y="y", hue="treated", legend=None, ax=ax1)
sns.lineplot(data=obs_df.assign(y=obs_df["y"] + baseline).query("treated==0"),
x="period", y="y", legend=None, ax=ax1, color="C0", linestyle="dotted")
sns.scatterplot(data=obs_df, x="period", y="y", hue="treated", style="treated", s=100, ax=ax1)
ax1.set_title("Parallel Trends")
plt_d2 = pd.DataFrame(dict(
period = [1,2,3,4, 1,2,3,4],
treated = [0,0,0,0, 1,1,1,1],
y = [2,4,6,8, 9,10,11,12],
))
sns.lineplot(data=plt_d2, x="period", y="y", hue="treated", linestyle="dashed", legend=None, ax=ax2)
sns.lineplot(data=obs_df, x="period", y="y", hue="treated", legend=None, ax=ax2)
sns.scatterplot(data=obs_df, x="period", y="y", hue="treated", style="treated", s=100, ax=ax2)
sns.lineplot(data=obs_df.assign(y=obs_df["y"] + baseline).query("treated==0"),
x="period", y="y", legend=None, ax=ax2, color="C0", linestyle="dotted")
ax2.set_title("Diverging Trends")
non_lin = np.log
non_lin_obs = obs_df.assign(y=non_lin(obs_df["y"]))
plt_d3 = pd.DataFrame(dict(
period = [1,2,3,4, 1,2,3,4],
treated = [0,0,0,0, 1,1,1,1],
y = non_lin([2,4,6,8, 8,10,12,14]),
))
sns.lineplot(data=plt_d3, x="period", y="y", hue="treated", linestyle="dashed", legend=None, ax=ax3)
sns.lineplot(data=non_lin_obs, x="period", y="y", hue="treated", legend=None, ax=ax3)
sns.scatterplot(data=non_lin_obs, x="period", y="y", hue="treated", style="treated", s=100, ax=ax3)
sns.lineplot(x=[2, 3], y=non_lin_obs.query("treated==1 & period==2")["y"].values - non_lin_obs.query("treated==0 & period==2")["y"].values + non_lin_obs.query("treated==0")["y"], color="C0",
linestyle="dotted")
ax3.set_title("Log Scale")
ax3.set_ylabel("Log(y)")
Text(0, 0.5, 'Log(y)')
在第一个图表中,估算的 Y ( 0 ) ∣ D = 1 Y(0)|D=1 Y(0)∣D=1 与实际值重合。在这种情况下,平行趋势假设得到满足,双重差分估算器恢复了真实的ATT。在第二个图表中,趋势收敛。对于 Y ( 0 ) ∣ D = 1 Y(0)|D=1 Y(0)∣D=1,估算的趋势比实际趋势更陡峭。因此,双重差分的估算会产生向下的偏差: E ( Y ( 1 ) ∣ D = 1 , P o s t = 1 ) E(Y(1)|D=1,Post=1) E(Y(1)∣D=1,Post=1) 与估算趋势之间的差异小于 E ( Y ( 1 ) ∣ D = 1 , P o s t = 1 ) E(Y(1)|D=1,Post=1) E(Y(1)∣D=1,Post=1) 与实际的、但不可观测的 E ( Y ( 0 ) ∣ D = 1 , P o s t = 1 ) E(Y(0)|D=1,Post=1) E(Y(0)∣D=1,Post=1) 之间的差异。
最后一张图表展示了平行趋势假设是如何不具有尺度不变性的。这个图表简单地将第一个图表的数据进行了对数转换。这种转换将原本平行的趋势变得收敛。我展示这个是为了提醒你在使用双重差分时要非常小心。例如,如果你有的是水平数据,但想要测量其作为百分比变化的效果,将结果转换为百分比可能会扰乱你的趋势。
另请参阅
在论文《何时平行趋势对函数形式敏感?》(When Is Parallel Trends Sensitive to Functional Form?)中,Jonathan Roth和Pedro Sant’Anna推导出了一个更严格的平行趋势版本,该版本对结果的单调变换是不变的,并讨论了该假设在何种情况下是合理的。
关于平行趋势假设的另一种思考方式是将其与条件独立假设(CIA)联系起来。虽然CIA表明 Y ( 0 ) Y(0) Y(0) 的水平,在干预组和对照组中平均而言是相同的,但平行趋势表明 Y ( 0 ) Y(0) Y(0) 的增长在干预组和对照组之间是相同的。这可以用你之前看到的 Δ Y \Delta Y ΔY 来表示:
( Δ y 0 , Δ y 1 ) ⊥ T (\Delta y_0,\Delta y_1) \perp T (Δy0,Δy1)⊥T
这就是面板数据的力量:即使干预不是随机分配的,只要干预组和对照组具有相同的反事实增长,ATT就可以被识别。
与独立假设一样,你可以放宽平行趋势假设,使其以协变量为条件。也就是说,给定一组预干预协变量 X X X, Y ( 0 ) Y(0) Y(0) 的趋势在干预组和对照组之间是相同的。你将在本章后面看到如何在DID中纳入协变量。
8.3.2 无预期假设(No Anticipation Assumption)与SUTVA
如果将平行趋势假设视为独立假设的面板数据版本,那么无预期假设则更与干预的稳定单元干预值假设(SUTVA)相关。回忆一下,当效果从干预组溢出到对照组(或反之)时,就会出现SUTVA违规。那么,在这里,情况是相同的,但跨越了不同的时间段:你不希望在干预尚未发生的时候,效果就溢出到其他时期。
如果你认为这不可能发生,那就考虑一下你正在尝试评估黑色星期五对手机销售的影响。如果你尝试这样做,你会发现许多商家会预期黑色星期五的折扣,他们知道黑色星期五之前的这段时间是顾客已经在购买产品的时期。这很可能导致你在干预(黑色星期五)发生之前就看到销售额的激增。
事实上,你必须担心时间溢出并不意味着你不必担心单元溢出。在面板数据分析中,老的SUTVA仍然是一个大问题,特别是当单元是一个地理区域时。那是因为人们不断跨越地理边界,这使得干预很可能从被干预的单元中溢出。
空间溢出
与面板数据文献中的所有内容一样,处理空间溢出是因果推断领域仍在研究的内容。Kyle Butts撰写的《具有空间溢出的双重差分估算》(Difference-in-Differences Estimation with Spatial Spillovers)是一篇关于这个主题的非常好的论文。这篇论文不难阅读,提出的解决方案也易于实施。基本的想法是用一个虚拟变量 S S S 来扩展DID的双向固定效应公式,如果对照单元被认为足够接近干预单元,则 S S S 为1:
Y i t = τ i t W i t + η 0 S i ( 1 − W i t ) + η 1 S i W i t + α i + γ t + e i t Y_{it}=\tau_{it}W_{it} +\eta_0 S_i (1-W_{it}) +\eta_1 S_i W_{it} +\alpha_i +\gamma_t +e_{it} Yit=τitWit+η0Si(1−Wit)+η1SiWit+αi+γt+eit
8.3.3 严格外生性(Strict Exogeneity)
严格外生性假设是一个非常技术性的假设,通常用固定效应模型的残差来表示:
Y i t = α i + X i t β + ϵ i t Y_{it}=\alpha_i +X_{it} \beta +\epsilon_{it} Yit=αi+Xitβ+ϵit
严格外生性表明:
E ( ϵ i t ∣ X i t , α i ) = 0 E(\epsilon_{it}|X_{it},\alpha_i)=0 E(ϵit∣Xit,αi)=0
这个假设更强,意味着平行趋势。它也相当晦涩,所以我认为我们最好从它所暗示的方面来讨论:
- 无随时间变化的混淆因子
- 无反馈
- 无延续效应
你还可以通过在DAG中展示这一假设,使其更易于理解:
现在,让我们来看看它的真正含义。
8.3.4 无时间变化混淆因子(No Time Varying Confounders)
让我先告诉大家一个好消息。还记得我提到过,面板数据可以利用时间和单元之间的相关性吗?值得注意的是,随着时间的推移,反复的观测可以帮助你确定因果关系,即使存在未观察到的混淆因子。只要这些混淆因素随时间保持不变或在所有单元中保持一致,上述结论就成立。为了更好地理解这一点,让我们再次审视市场营销的例子。每个城市都有其独特的文化、法律和人口,所有这些都可能对干预变量和结果变量产生重大影响。其中一些变量,如文化和法律,是难以量化的,这使它们成为需要考虑的未观测混淆因子。然而,当你不能测量它们时,你如何做到这一点呢?
关键在于,通过聚焦一个单元并追踪它随时间的变化,你已经在控制任何与时间固定的因子。这包括任何与时间固定的混淆因子,甚至是那些未测量的。在市场营销的例子中,如果某个城市的下载量随着时间的推移而增加,你就知道这不可能是因为城市文化的任何变化(至少不是在短时间内),仅仅是因为这个混淆因子是随时间固定的。底线是,即使你不能控制与时间固定的混淆因子,因为你无法测量它,但如果你控制了单元本身,你仍然可以截断通过它的后门路径。
如果你更偏向数学思维,你也能明白处理数据的过程是如何消除任何与时间固定的协变量的。回忆一下,添加单元固定效应可以通过添加单元虚拟变量来实现,也可以通过计算单元的结果和干预的平均值,并从原始变量中减去这些平均值来实现:
Y ¨ i t = Y i t − Y ‾ i W ¨ i t = W i t − W ‾ i \ddot{Y}_{it}=Y_{it}-\overline Y_i \\ \ddot{W}_{it}=W_{it}-\overline W_i Y¨it=Yit−YiW¨it=Wit−Wi
在这里,我用 W i t = D i P o s t t W_{it}=D_i Post_t Wit=DiPostt来表示干预,因为 D i D_i Di 是时间固定的。通过去均值化,任何未观察到的 U i U_i Ui 都会消失。由于 U i U_i Ui 在时间上是恒定的,你有 U i = U ‾ i U_i=\overline U_i Ui=Ui,这使得 U ¨ i t = 0 \ddot{U}_{it}=0 U¨it=0 处处成立。简而言之,单元固定效应消除了任何在时间上恒定的变量。
我现在关注的是单元固定效应,但类似的论据也可以用来展示时间固定效应是如何消除任何在单元间恒定但随时间变化的变量的。在我们的例子中,这些可能是国家的汇率或通货膨胀率。由于这些都是全国性的变量,它们对所有城市都是相同的。
当然,如果未观察到的混淆因子随时间和单元而变化,那么在这里就没有太多可以做的了。
8.3.5 无反馈(No Feedback)
你可能已经注意到,前面的图中有另一个关键的假设。具体来说,没有箭头从过去的结果 Y i t − 1 Y_{it-1} Yit−1 延伸到当前的干预 W i t W_{it} Wit。换句话说,就是没有反馈。这意味着干预不能基于结果轨迹来决定。举例来说,假设干预是一个由时间索引的向量 W = ( ω 0 , ω 1 , . . . , ω T ) W=(\omega_0,\omega_1,...,\omega_T) W=(ω0,ω1,...,ωT),在这种情况下,整个向量必须一次性决定。这在你之前看到的块状设计中是可行的,其中干预在某个特定时间段启动并无限期持续。然而,即使如此,无反馈假设也可能被违反。例如,假设营销团队决定,每当一个城市的下载量达到1000次时,他们将进行一次线下营销活动。这将违反无反馈假设。
时序可忽略性
如果你希望能够对过去的结果设置条件,你需要研究在时序可忽略性下工作的方法。遗憾的是,你只能控制过去的结果或时间固定的混淆因子,而不能同时控制两者。要了解更多关于这个主题的信息,建议你查阅Yiqing Xu的论文《基于时间序列横截面数据的因果推断:反思》(Causal Inference with Time-Series Cross-Sectional Data: A Reflection),或M.A.赫尔南(M.A. Hernán)和J.M.罗宾斯(J.M. Robins)合著的《因果推断》(Causal Inference)一书。
8.3.6 无延续效应(No Carryover)因变量和无滞后(no Lagged)因变量
除了无反馈外,你还可能会观察到,该图还假设没有延续效应,因为没有箭头从过去的干预指向当前的结果。幸运的是,如果你扩展模型,包括干预的滞后版本,这种假设就可以放宽。例如,如果您认为 t − 1 t-1 t−1 周期的干预会在 t t t 时影响结果,你可以使用以下模型:
Y i t = τ i t W i t + θ W i t − 1 + α i + γ t + e i t Y_{it}=\tau_{it} W_{it} +\theta W_{it-1} +\alpha_i +\gamma_t +e_{it} Yit=τitWit+θWit−1+αi+γt+eit
最后,该图还假设没有滞后因变量,这意味着过去的结果不会直接影响当前的结果。对你来说幸运的是,这种假设并不是真的必要;增加从过去的 Y Y Y 到未来的 Y Y Y 的箭头并不会妨碍识别。
另请参阅
在DAG中表示面板数据并不是一件微不足道的事情,但有两篇伟大的论文试图这样做。它们真的帮助我理解了严格外生性所意味的东西。第一,Imai和Kim的论文《我们何时应该使用单元固定效应回归模型对纵向数据进行因果推断?》(When Should We Use Unit Fixed Effects Regression Models for Causal Inference with Longitudinal Data?)。第二,Yiqing Xu的论文《基于时间序列横截面数据的因果推断:反思》(Causal Inference with Time-Series Cross-Sectional Data: A Reflection)。
8.4 效果时间动力学(Effect Dynamics Over Time)
到现在为止,你可能已经对典型的双重差分法(DID)有了相当深入的理解,这意味着你现在可以尝试从典型双重差分法深入到更隐秘的变体。一个稍微复杂一些的方法是纳入效果时间动力学时。如果你回顾展示结果演变的图表,你会发现干预组和对照组之间的差异并不会在干预后立即增加。相反,干预需要一些时间才能达到完全的效果。换句话说,干预效果不是瞬时生效的。这种现象不仅在营销中相当常见,而且对整个地区的任何干预措施也是如此。这也意味着你可能会低估最终的干预效果,因为你包括了干预效果尚未完全成熟的时间段。
解决这个问题的一个简单方法是随时间估算ATT。如果你足够聪明,可以通过为每个干预后周期创建虚拟变量来实现这一点,但我最喜欢的随时间获取干预效果的方式是使用一些蛮力:遍历所有周期,假设只有当前周期是处理后的周期,运行双重差分法。
为了做到这一点,让我们创建一个函数,它接收一个数据框和一个日期,并运行双重差分法,假装这个日期是干预后的周期:
def did_date(df, date):
df_date = (df
.query("date==@date | post==0")
.query("date <= @date")
.assign(post = lambda d: (d["date"]==date).astype(int)))
m = smf.ols(
'downloads ~ I(treated*post) + C(city) + C(date)', data=df_date
).fit(cov_type='cluster', cov_kwds={'groups': df_date['city']})
att = m.params["I(treated * post)"]
ci = m.conf_int().loc["I(treated * post)"]
return pd.DataFrame({"att": att, "ci_low": ci[0], "ci_up": ci[1]},
index=[date])
首先,这个函数仅过滤干预前的周期和传入的日期。接下来,它过滤等于或早于传入日期的周期。如果传入的日期来自干预后周期,这个过滤是无害的。如果日期来自干预前的周期,它会丢弃该日期之后的周期。这允许你对干预前的周期运行双重差分法。实际上,要做到这一点,你需要下一行代码,其中函数将干预后周期重新指定为特定周期。现在,如果你传入的日期来自干预前,函数将假装它来自干预后周期,这在时间维度上是一种安慰剂测试。最后,函数估算一个双重差分模型,提取ATT和其置信区间。然后,将所有内容存储在单行数据框中。
这个函数适用于单个日期。要获取所有可能日期的效果,你可以遍历这些日期,每次获取双重差分的估算值。只需记住,你需要跳过第一个日期,因为运行双重差分至少需要两个周期。如果你将所有结果存储在一个列表中,你可以在该列表上调用pd.concat来将所有结果合并到一个数据框中:
post_dates = sorted(mkt_data["date"].unique())[1:]
atts = pd.concat([did_date(mkt_data, date)
for date in post_dates])
atts.head()
| att | ci_low | ci_up | |
|---|---|---|---|
| 2021-05-02 | 0.325397 | -0.491741 | 1.142534 |
| 2021-05-03 | 0.384921 | -0.388389 | 1.158231 |
| 2021-05-04 | -0.156085 | -1.247491 | 0.935321 |
| 2021-05-05 | -0.299603 | -0.949935 | 0.350729 |
| 2021-05-06 | 0.347619 | 0.013115 | 0.682123 |
然后,你可以将干预效果随时间的变化以及其置信区间绘制出来。这张图表明,在干预发生后,干预效果并没有上升。而且,如果你丢弃早期干预效果尚未完全成熟的时间段,ATT似乎会略微提高一些。同时,我也绘制了真实的效果 τ \tau τ,这样你可以看到这种方法是如何相当准确地恢复 τ \tau τ 的:
plt.figure(figsize=(10,4))
plt.plot(atts.index, atts["att"], label="Est. ATTs")
plt.fill_between(atts.index, atts["ci_low"], atts["ci_up"], alpha=0.1)
plt.vlines(pd.to_datetime("2021-05-15"), -2, 3, linestyle="dashed", label="intervention")
plt.hlines(0, atts.index.min(), atts.index.max(), linestyle="dotted")
plt.plot(atts.index, mkt_data.query("treated==1").groupby("date")[["tau"]].mean().values[1:], color="0.6", ls="-.", label="$\\tau$")
plt.xticks(rotation=45)
plt.title("DID ATTs Over Time")
plt.legend()
这个图表的干预前部分也值得你的关注。在此期间,所有估算的效果都与零无异,这表明在处理之前并没有效果产生。这为无预期假设(No-anticipation Assumption)在这种情况下可能有效提供了有力证据。
8.5 带有协变量的双重差分法(Diff-in-Diff with Covariates)
你需要学习的DID的另一个变化是如何在模型中包含干预前的协变量。当怀疑平行趋势不成立,但条件平行趋势成立时,这非常有用:
E ( Y ( 0 ) i t = 1 − Y ( 0 ) i t = 0 ∣ D = 1 , X ) = E ( Y ( 0 ) i t = 1 − Y ( 0 ) i t = 0 ∣ D = 0 , X ) E(Y(0)_{it=1} -Y(0)_{it=0}|D=1,X) =E(Y(0)_{it=1} -Y(0)_{it=0}|D=0,X) E(Y(0)it=1−Y(0)it=0∣D=1,X)=E(Y(0)it=1−Y(0)it=0∣D=0,X)
考虑以下情况:还是以前相同的营销数据,但现在,你拥有全国多个区域的数据。如果为每个区域绘制干预组和控制组的结果,你会发现一些有趣的现象:
mkt_data_all = (pd.read_csv("./data/short_offline_mkt_all_regions.csv")
.astype({"date":"datetime64[ns]"}))
plt.figure(figsize=(15,6))
sns.lineplot(data=mkt_data_all.groupby(["date", "region", "treated"])[["downloads"]].mean().reset_index(),
x="date", y="downloads", hue="region", style="treated", palette="gray")
plt.vlines(pd.to_datetime("2021-05-15"), 15, 55, ls="dotted", label="Intervention")
plt.legend(fontsize=14)
plt.xticks(rotation=25);
干预前趋势在一个区域内似乎是平行的,但在不同区域间则不然。因此,如果你直接在这里运行DID的双向固定效应模型,你将得到ATT的有偏估计:
print("True ATT: ", mkt_data_all.query("treated*post==1")["tau"].mean())
m = smf.ols('downloads ~ treated:post + C(city) + C(date)',
data=mkt_data_all).fit()
print("Estimated ATT:", m.params["treated:post"])
True ATT: 1.7208921056102682
Estimated ATT: 2.068391984256296
你需要以某种方式考虑到每个区域的不同趋势。你可能会认为,只需在回归中将区域作为额外的协变量添加进去就能解决问题。但请三思!还记得使用单元固定效应时会如何消除任何时间固定协变量的效应吗?这不仅适用于不可观测的混淆因子,也适用于随时间恒定的区域协变量。最终结果是,简单地将其添加到回归中是无效的。你会得到与之前相同的结果:
m = smf.ols('downloads ~ treated:post + C(city) + C(date) + C(region)',
data=mkt_data_all).fit()
m.params["treated:post"]
2.071153674125536
因此,为了得到更准确的估计,我们需要通过在模型中加入干预前协变量来考虑到这些不同区域的不同趋势。这样可以使我们更好地理解和评估干预措施对结果的影响,减少偏差并增加估算的准确性。同时,这也是在处理具有多个区域或子群体数据时的一个重要步骤,以确保我们充分利用了可用的信息,并得到了可靠的结论:
m_saturated = smf.ols('downloads ~ (post*treated)*C(region)',
data=mkt_data_all).fit()
atts = m_saturated.params[m_saturated.params.index.str.contains("post:treated")]
atts
post:treated 1.676808
post:treated:C(region)[T.N] -0.343667
post:treated:C(region)[T.S] -0.985072
post:treated:C(region)[T.W] 1.369363
dtype: float64
记住,ATT的估算值应相对于基线组进行解释,在这种情况下,基线组是东部地区。因此,对北区的影响是1.67–0.34,对南区的影响是1.67–0.98,以此类推。接下来,你可以使用加权平均数汇总不同的ATT,其中地区的城市数量就是权重:
reg_size = (mkt_data_all.groupby("region").size()
/len(mkt_data_all["date"].unique()))
base = atts[0]
np.array([reg_size[0]*base]+
[(att+base)*size
for att, size in zip(atts[1:], reg_size[1:])]
).sum()/sum(reg_size)
1.6940400451471818
尽管我说这是过度的,但实际上这是一个非常好的想法。它非常容易实施,也很难出错。然而,它仍然存在一些问题。例如,如果你有许多协变量或连续协变量,这种方法将是不切实际的。这就是为什么我认为你应该知道还有另一种方法。不是将地区与干预后虚拟变量和干预虚拟变量相互作用,你可以仅与干预后虚拟变量相互作用。这个模型将分别估算每个地区干预的趋势(干预前和干预后的结果水平),但它将对干预周期和干预后周期拟合一个单一的截距变化:
m = smf.ols('downloads ~ post*(treated + C(region))',
data=mkt_data_all).fit()
m.summary().tables[1]
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 17.3522 | 0.101 | 172.218 | 0.000 | 17.155 | 17.550 |
| C(region)[T.N] | 26.2770 | 0.137 | 191.739 | 0.000 | 26.008 | 26.546 |
| C(region)[T.S] | 33.0815 | 0.135 | 245.772 | 0.000 | 32.818 | 33.345 |
| C(region)[T.W] | 10.7118 | 0.135 | 79.581 | 0.000 | 10.448 | 10.976 |
| post | 4.9807 | 0.134 | 37.074 | 0.000 | 4.717 | 5.244 |
| post:C(region)[T.N] | -3.3458 | 0.183 | -18.310 | 0.000 | -3.704 | -2.988 |
| post:C(region)[T.S] | -4.9334 | 0.179 | -27.489 | 0.000 | -5.285 | -4.582 |
| post:C(region)[T.W] | -1.5408 | 0.179 | -8.585 | 0.000 | -1.893 | -1.189 |
| treated | 0.0503 | 0.117 | 0.429 | 0.668 | -0.179 | 0.280 |
| post:treated | 1.6811 | 0.156 | 10.758 | 0.000 | 1.375 | 1.987 |
与post:treated相关的参数可以解释为ATT,与你之前得到的ATT并不完全相同,但非常接近。出现差异的原因在于,回归分析通过方差对各区域的ATT进行平均,而之前你通过区域大小进行平均。这意味着回归分析将更加重视干预分布更均匀的区域(具有更高的方差)。
第二种方法运行起来更快,但缺点是它要求你仔细思考如何进行交互。因此,我建议你只在你真正知道自己在做什么的情况下使用它。或者,在使用它之前,尝试构建一些模拟数据,这样你知道真实的ATT,看看是否能够通过你的模型恢复它。记住:对每个区域运行一个DID模型并平均结果并不丢人。事实上,这是一个特别聪明的想法。
8.6 双重鲁棒性双重差分法(Doubly Robust Diff-in-Diff)
另一种结合干预前和时间不变协变量以允许条件平行趋势的方法是制作双重差分法的双重鲁棒版本(DRDID)。为此,你可以借鉴第5章中的许多想法,学习如何构建双重鲁棒估算量。然而,你需要做一些调整。首先,由于DID适用于 Δ y \Delta y Δy,因此你需要的不仅是原始结果模型,还需要一个随时间变化的结果增量模型。其次,由于你只关心ATT,你只需要从对照单元中重建干预过的人群。当我向你展示构建DRDID的步骤时,所有这些都将更有意义。
8.6.1 倾向得分模型
DRDID的第一步是构建倾向得分模型 e ^ ( X ) \hat e(X) e^(X),这个模型使用干预前协变量来估算一个单元是干预组的概率。这个模型不关心时间维度,这意味着你只需要使用一段时间的数据来估算它:
import warnings
warnings.filterwarnings('ignore')
unit_df = (mkt_data_all
# keep only the first date
.astype({"date": str})
.query(f"date=='{mkt_data_all['date'].astype(str).min()}'")
.drop(columns=["date"])) # just to avoid confusion
ps_model = smf.logit("treated~C(region)", data=unit_df).fit(disp=0)
8.6.2 结果增量模型(Delta Outcome Model)
接下来,你需要为 Δ y \Delta y Δy 构建结果模型,这意味着你首先需要构建结果增量数据。为此,你需要计算干预前和干预后周期的平均结果的差值。完成这一步后,由于时间维度已经被消除,你最终将得到每个单元只有一行的数据:
delta_y = (
mkt_data_all.query("post==1").groupby("city")["downloads"].mean()
- mkt_data_all.query("post==0").groupby("city")["downloads"].mean()
)
现在你有了 Δ y \Delta y Δy,你可以将它与单元数据集合并,并在其中拟合结果模型。
df_delta_y = (unit_df
.set_index("city")
.join(delta_y.rename("delta_y")))
outcome_model = smf.ols("delta_y ~ C(region)", data=df_delta_y).fit()
8.6.3 整合所有步骤
现在是把所有部分整合起来的时候了。首先,让我们将你所需要的所有数据收集到一个数据框中。对于最终的估算器,你需要实际的 Δ y \Delta y Δy、倾向性得分和结果增量预测。为此,你可以从用于构建结果模型的df_delta_y开始,同时使用倾向性得分模型 e ^ ( x ) \hat e(x) e^(x) 和结果模型 m ^ ( x ) \widehat m(x) m (x) 进行预测。结果再次是一个单元级别的数据框:
df_dr = (df_delta_y
.assign(y_hat = lambda d: outcome_model.predict(d))
.assign(ps = lambda d: ps_model.predict(d)))
df_dr.head()
| region | treated | tau | downloads | post | delta_y | y_hat | ps | |
|---|---|---|---|---|---|---|---|---|
| city | ||||||||
| 1 | W | 0 | 0.0 | 27.0 | 0 | 3.087302 | 3.736539 | 0.176471 |
| 2 | N | 0 | 0.0 | 40.0 | 0 | 1.436508 | 1.992570 | 0.212766 |
| 3 | W | 0 | 0.0 | 30.0 | 0 | 2.761905 | 3.736539 | 0.176471 |
| 4 | W | 0 | 0.0 | 26.0 | 0 | 3.396825 | 3.736539 | 0.176471 |
| 5 | S | 0 | 0.0 | 51.0 | 0 | -0.476190 | 0.343915 | 0.176471 |
好的,让我们思考一下双重鲁棒的DID会是什么样子。与所有的DID一样,ATT估算是在单元受到干预的情况下的趋势和对照组的趋势之间的差异。由于这些是反事实的量,我将用 Δ y 1 \Delta y_1 Δy1 和 Δ y 0 \Delta y_0 Δy0 分别表示它们。因此,综上所述,ATT可以由以下公式给出:
τ D R D I D = Δ y ^ 1 D R − Δ y ^ 0 D R \tau_{DRDID}=\widehat{\Delta y}_1^{DR} -\widehat{\Delta y}_0^{DR} τDRDID=Δy 1DR−Δy 0DR
我承认,这进展并不多,但这是一个很好的开始。接下来,你需要思考如何以双重鲁棒的方式估算 Δ y D \Delta y_D ΔyD。
让我们关注 Δ y 1 \Delta y_1 Δy1。为了估算干预组的反事实结果,你将使用倾向性得分的倒数对 y − m ^ ( x ) y-\widehat m(x) y−m (x) 进行加权,这将为整个人群重构 y 1 y_1 y1(见第5章)。在这里,由于你只关心ATT,你不需要这个;你已经得到了干预人群。因此,第一项变为:
Δ y ^ 1 D R = 1 / N t r ∑ i ∈ t r ( Δ y − m ^ ( X ) ) \widehat{\Delta y}_1^{DR}=1/N_{tr} \sum_{i \in tr}(\Delta y -\widehat m(X)) Δy 1DR=1/Ntri∈tr∑(Δy−m (X))
对于另一项,你将使用权重 1 / ( 1 − e ^ ( x ) ) 1/(1-\hat e(x)) 1/(1−e^(x)) 来在控制下重建总体人群。但是,同样,由于你关心的是ATT,你需要在控制下重建干预人群。要做到这一点,你可以简单地将权重乘以单元被干预的概率,这恰巧就是倾向性得分:
ω c o = e ^ ( X ) 1 1 − e ^ ( X ) \omega_{co}=\hat e(X) \frac{1}{1-\hat e(X)} ωco=e^(X)1−e^(X)1
定义了权重之后,你可以用它来获得 Δ y 0 \Delta y_0 Δy0 的估算:
Δ y ^ 0 D R = ∑ i ∈ c o ω c o ( Δ y − m ^ ( X ) ) / ∑ ω c o \widehat{\Delta y}_0^{DR}=\sum_{i \in co} {\omega_{co} (\Delta y -\widehat m(X))}/ \sum {\omega_{co}} Δy 0DR=i∈co∑ωco(Δy−m (X))/∑ωco
差不多就这样了。和往常(几乎)一样,代码看起来比数学推导简单得多:
tr = df_dr.query("treated==1")
co = df_dr.query("treated==0")
dy1_treat = (tr["delta_y"] - tr["y_hat"]).mean()
w_cont = co["ps"]/(1-co["ps"])
dy0_treat = np.average(co["delta_y"] - co["y_hat"], weights=w_cont)
print("ATT:", dy1_treat - dy0_treat)
ATT: 1.6773180394442853
它与真实的ATT以及你早些时候将协变量添加到DID时得到的ATT非常接近。这里的优势在于你有两次机会来正确估算。只要倾向性得分模型或结果模型中有一个(但不必两者都)是正确的,DRDID就能发挥作用。为避免本章内容过长,在此我不再赘述,但我鼓励你尝试将ps列或y_hat列替换为随机生成的列,并重新计算前面的估算值。你会发现最终结果仍然接近实际值。
另请参阅
Sant’Anna和Zhao在论文《双重鲁棒的差分估计器》(Doubly Robust Difference-in-Differences Estimators)中提出了这种方法。该论文包含了更多内容,包括如何使用该估算器进行推理,以及如何在重复横截面数据(每个时间段的单元可以变化)相对于面板数据(所有单元相同)时实现双重鲁棒性。
就像你在横截面数据中进行双重鲁棒估算一样,要获得DRDID的置信区间,你需要使用之前实现的块自助函数,将整个过程(结果模型、倾向性评分模型,以及将它们组合在一起)封装在一个单一的估算函数中。
8.7 交错采纳设计(Staggered Adoption)
到目前为止,你所关注的数据类型遵循了块设计,只有两个周期:干预前和干预后。尽管每个周期都有多个日期,但最终重要的是,您有一组在相同时间点接受处理的单元和一组从未干预的单元。这种块设计是双重差分分析中的典范,因为它使事情变得非常简单,允许你非参数化地估算基线和趋势,即通过简单计算一组样本平均值并进行比较。但其也可能有相当大的局限性。如果干预在不同的时间点推广到各个单元,那该怎么办?
面板数据中更常见的情况是交错采纳设计,在这种情况下,你有多个单元分组,我将其称为 G G G,每个组在不同的时间点(或从不)接受干预。由于采用干预的时间来定义分组,因此通常这样给这些群体命名:在 t t t 时间接受干预的 G G G 组是 G t G_t Gt 群体。
将其带到你一直关注的营销数据,你有两个群体:一个从未接受过干预的群体, G ∞ G_∞ G∞,和一个在2021-05-15接受干预的群体, G 15 / 05 G{15/05} G15/05。但这只是因为我隐藏了2021-06-01之后发生的事情。既然你已经准备好应对更复杂的情况,请查看mkt_data_cohorts数据框,它也包含所有地区的城市数据,但日期一直到2021-07-31:
mkt_data_cohorts = (pd.read_csv("./data/offline_mkt_staggered.csv")
.astype({
"date":"datetime64[ns]",
"cohort":"datetime64[ns]"}))
mkt_data_cohorts.head()
| date | city | region | cohort | treated | tau | downloads | post | |
|---|---|---|---|---|---|---|---|---|
| 0 | 2021-05-01 | 1 | W | 2021-06-20 | 1 | 0.0 | 27.0 | 0 |
| 1 | 2021-05-02 | 1 | W | 2021-06-20 | 1 | 0.0 | 28.0 | 0 |
| 2 | 2021-05-03 | 1 | W | 2021-06-20 | 1 | 0.0 | 28.0 | 0 |
| 3 | 2021-05-04 | 1 | W | 2021-06-20 | 1 | 0.0 | 26.0 | 0 |
| 4 | 2021-05-05 | 1 | W | 2021-06-20 | 1 | 0.0 | 28.0 | 0 |
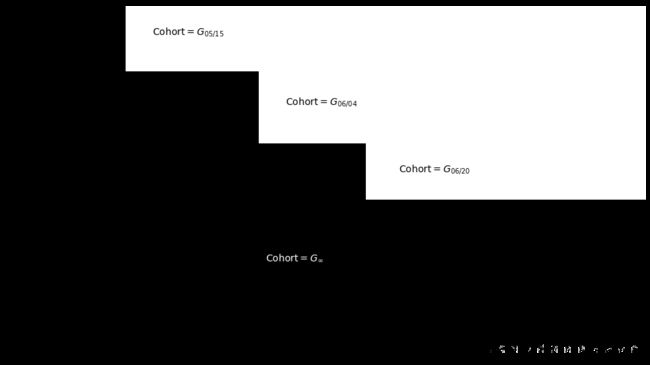
仅仅通过查看前几行数据是很难观察到数据全貌的,但是下图展示了随时间变化的干预状态,你可以看到交错采纳设计是什么样子。
plt_data = (mkt_data_cohorts
.astype({"date":"str"})
.assign(treated_post = lambda d: d["treated"]*(d["date"]>=d["cohort"]))
.pivot("city", "date", "treated_post")
.reset_index()
.sort_values(list(sorted(mkt_data_cohorts.query("cohort!='2100-01-01'")["cohort"].astype("str").unique())), ascending=False)
.reset_index()
.drop(columns=["city"])
.rename(columns={"index":"city"})
.set_index("city"))
plt.figure(figsize=(16,8))
sns.heatmap(plt_data, cmap="gray",cbar=False)
plt.text(18, 18, "Cohort$=G_{05/15}$", size=14)
plt.text(38, 65, "Cohort$=G_{06/04}$", size=14)
plt.text(55, 110, "Cohort$=G_{06/20}$", size=14)
plt.text(35, 170, "Cohort$=G_{\\infty}$", color="white", size=14, weight=3);
之前,你的数据只到2021-06-01,所以看起来你有一个小的干预组和一个巨大的未干预组。但是一旦你扩展了你的数据,你可以看到线下市场营销活动随后推广到了其他城市。现在,你有四个不同的群体,其中三个接受了处理,一个从未接受过处理(在这个数据集中是2100-01-01群体)。
警告
就像块设计一样,交错采纳假设一旦干预开始,就会永远保持下去,保证事情易于管理。在面板数据分析中,潜在结果是通过向量来表示每个时间段的结果轨迹的, D ( Y d 1 , Y d 2 , . . . , Y d T ) D(Y_{d1},Y_{d2},...,Y_{dT}) D(Yd1,Yd2,...,YdT),而干预效果是通过对比其中两个轨迹来定义的。这意味着,如果你允许干预开启和关闭,那么大约有 2 T 2^T 2T 种方式来定义干预效果。
让我们一步一步来,暂时忘记协变量,只关注西部地区。稍后我将展示如何处理协变量。现在,只关注问题的交错采纳部分:
mkt_data_cohorts_w = mkt_data_cohorts.query("region=='W'")
mkt_data_cohorts_w.head()
| date | city | region | cohort | treated | tau | downloads | post | |
|---|---|---|---|---|---|---|---|---|
| 0 | 2021-05-01 | 1 | W | 2021-06-20 | 1 | 0.0 | 27.0 | 0 |
| 1 | 2021-05-02 | 1 | W | 2021-06-20 | 1 | 0.0 | 28.0 | 0 |
| 2 | 2021-05-03 | 1 | W | 2021-06-20 | 1 | 0.0 | 28.0 | 0 |
| 3 | 2021-05-04 | 1 | W | 2021-06-20 | 1 | 0.0 | 26.0 | 0 |
| 4 | 2021-05-05 | 1 | W | 2021-06-20 | 1 | 0.0 | 28.0 | 0 |
如果你绘制每个群体的平均下载量随时间变化的图形,就能看到一个清晰的画面。在2021年5月15日之后, G = 05 / 15 G=05/15 G=05/15 的结果显示下载量增加。对于 G = 06 / 04 G=06/04 G=06/04 和 G = 06 / 20 G=06/20 G=06/20 的群体也是如此。与此同时,从未接受过干预的群体在干预之前似乎与干预群体呈现出平行的趋势。另一个需要注意的是,干预效果需要一段时间才能显现,这一点你以前也见过。如果你将群体对齐后绘制结果,这一点变得更加清晰,你可以在第二张图中看到:
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(15, 10))
plt_data = (mkt_data_cohorts_w
.groupby(["date", "cohort"])
[["downloads"]]
.mean()
.reset_index()
)
for color, cohort in zip(["C0", "C1", "C2", "C3"], mkt_data_cohorts_w.query("cohort!='2100-01-01'")["cohort"].unique()):
df_cohort = plt_data.query("cohort==@cohort")
sns.lineplot(data=df_cohort, x="date", y="downloads",
label=pd.to_datetime(cohort).strftime('%Y-%m-%d'), ax=ax1)
ax1.vlines(x=cohort, ymin=25, ymax=50, color=color, ls="dotted", lw=3)
sns.lineplot(data=plt_data.query("cohort=='2100-01-01'"), x="date", y="downloads", label="$\infty$", lw=4, ls="-.", ax=ax1)
ax1.legend()
ax1.set_title("Multiple Cohorts - North Region");
plt_data = (mkt_data_cohorts_w
.assign(days_to_treatment = lambda d: (pd.to_datetime(d["date"])-pd.to_datetime(d["cohort"])).dt.days)
.groupby(["date", "cohort"])
[["downloads", "days_to_treatment"]]
.mean()
.reset_index()
)
for color, cohort in zip(["C0", "C1", "C2", "C3"], mkt_data_cohorts_w.query("cohort!='2100-01-01'")["cohort"].unique()):
df_cohort = plt_data.query("cohort==@cohort")
sns.lineplot(data=df_cohort, x="days_to_treatment", y="downloads",
label=pd.to_datetime(cohort).strftime('%Y-%m-%d'), ax=ax2)
ax2.vlines(x=0, ymin=25, ymax=50, color="black", ls="dotted", lw=3)
ax2.set_title("Multiple Cohorts (Aligned) - North Region")
ax2.legend();
plt.tight_layout()
你可能会说,前面的数据表现得非常好,很明显是模拟出来的。你甚至可能会得出结论,认为双重差分在恢复真实的平均处理效应方面不会有问题。那么,让我们来试试看吧:
twfe_model = smf.ols(
"downloads ~ treated:post + C(date) + C(city)",
data=mkt_data_cohorts_w
).fit()
true_tau = mkt_data_cohorts_w.query("post==1&treated==1")["tau"].mean()
print("True Effect: ", true_tau)
print("Estimated ATT:", twfe_model.params["treated:post"])
True Effect: 2.2625252108176266
Estimated ATT: 1.7599504780633743
如你所见,有些东西不对劲。效果似乎是向下倾斜的!这是怎么回事?
这个问题一直是最近关于面板数据的文献的核心问题。遗憾的是,如果我试图给你一个完整的解释,这一章会太长。我能做的是让你略知一二,如果你感兴趣的话,我可以给你提供更多的资源。这个问题的根源在于,当你进行交错采纳时,除了你之前看到的传统的DID假设外,你还需要假设效果在时间上是一致的。如前所述,这个数据并非如此。效果需要一段时间才能显现,这意味着在干预刚刚发生后,效果较低,之后逐渐上升。这种效果随时间的变化会导致ATT估算产生偏差。
让我们通过检查两组城市来理解为什么会这样。第一组,我将称之为早期干预组,在06/04接受了干预。第二组,我将称之为晚期干预组,在06/20接受了干预。你刚刚估算的双向固定效应模型实际上使用了一系列的2×2的双重差分运行,并将它们组合成一个最终的估算。在其中一次运行中,模型使用晚期干预组作为对照组来估计早期干预组的干预效果。这是有效的,因为晚期干预组可以被视为尚未干预的组。然而,模型也使用早期干预组作为对照组来估计晚期干预组的效果。这种方法是可以接受的,但前提条件是干预效果在时间上是不变的。你可以在下图中看到原因。该图显示了两种比较以及估算的反事实 Y 0 Y_0 Y0。值得注意的是,每个分组的作用在一张图中与另一张图中是相反的:
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(15, 10), sharex=True)
# fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 10))
cohort_erly='2021-06-04'
cohort_late='2021-06-20'
## Early vs Late
did_df = (mkt_data_cohorts_w
.loc[lambda d: d["date"].astype(str) < cohort_late]
.query(f"cohort=='{cohort_late}' | cohort=='{cohort_erly}'")
.assign(treated = lambda d: (d["cohort"] == cohort_erly)*1,
post = lambda d: (d["date"].astype(str) >= cohort_erly)*1))
m = smf.ols(
"downloads ~ treated:post + C(date) + C(city)",
data=did_df
).fit()
# print("Estimated", m.params["treated:post"])
# print("True", did_df.query("post==1 & treated==1")["tau"].mean())
plt_data = (did_df
.assign(installs_hat_0 = lambda d: m.predict(d.assign(treated=0)))
.groupby(["date", "cohort"])
[["downloads", "post", "treated", "installs_hat_0"]]
.mean()
.reset_index())
sns.lineplot(data=plt_data, x="date", y="downloads", hue="cohort", ax=ax1)
sns.lineplot(data=plt_data.query("treated==1 & post==1"),
x="date", y="installs_hat_0", ax=ax1, ls="-.", alpha=0.5, label="$\hat{Y}_0|T=1$")
ax1.vlines(pd.to_datetime(cohort_erly), 26, 38, ls="dashed")
ax1.legend()
ax1.set_title("Early vs Late")
# ## Late vs Early
did_df = (mkt_data_cohorts_w
.loc[lambda d: d["date"].astype(str) > cohort_erly]
.query(f"cohort=='{cohort_late}' | cohort=='{cohort_erly}'")
.assign(treated = lambda d: (d["cohort"] == cohort_late)*1,
post = lambda d: (d["date"].astype(str) >= cohort_late)*1))
m = smf.ols(
"downloads ~ treated*post + C(date) + C(city)",
data=did_df
).fit()
# print("Estimated", m.params["treated:post"])
# print("True", did_df.query("post==1 & treated==1")["tau"].mean())
plt_data = (did_df
.assign(installs_hat_0 = lambda d: m.predict(d.assign(treated=0)))
.groupby(["date", "cohort"])
[["downloads", "post", "treated", "installs_hat_0"]]
.mean()
.reset_index())
sns.lineplot(data=plt_data, x="date", y="downloads", hue="cohort", ax=ax2)
sns.lineplot(data=plt_data.query("treated==1 & post==1"),
x="date", y="installs_hat_0", ax=ax2, ls="-.", alpha=0.5, label="$\hat{Y}_0|T=1$")
ax2.vlines(pd.to_datetime("2021-06-20"), 32, 45, ls="dashed")
ax2.legend()
ax2.set_title("Late vs Early")
Text(0.5, 1.0, 'Late vs Early')
正如你所看到的,早期与晚期的比较似乎没有问题。问题出在晚期与早期的比较上。尽管对照组(06/04群组)在此处作为对照组,但它已经受到了干预。此外,由于干预效果是异质性的,逐渐攀升,对照组(早期干预组)的趋势比该群组尚未受到干预时的趋势更陡峭。这种逐渐增加的额外陡峭度导致了对控制趋势的高估,这进而转化为向下偏误的ATT估计。这就是为什么如果干预效果随时间变化而具有异质性,使用已干预的群组作为对照会导致结果产生偏差。
另请参阅
就像我说的,最近有很多关于双向固定效应模型这种局限性的文献。如果你想了解更多,我强烈推荐Andrew Goodman-Bacon的论文《干预时间的变化的双重差分》(Difference-in-Differences with Variation in Treatment Timing)。他对问题的诊断非常简洁直观。更不用说,它还配有漂亮的图片,有助于对论文的整体理解。
现在你已经知道了问题所在,是时候寻找解决方案了。由于问题出在效果的异质性上,解决方法将是使用一个更灵活的模型,这个模型充分考虑到了这些异质性。
高等教育与发展中国家的增长
在最近的一篇论文《越南高等教育扩张、劳动力市场和企业生产率》(Higher Education Expansion, Labor Market, and Firm Productivity in Vietnam)中,Khoa Vu和Tu-Anh Vu-Thanh研究了越南大学数量的快速增长,以弄清高等教育对工资的影响。他们利用高等教育扩张对各省的影响不同,通过差分法识别了大学的影响。
我们收集了一个关于大学开办时间和地点的数据集,并估算个人接触大学开办的机会增加了他们完成大学学业的概率超过30%。它还使他们的工资提高了3.9%,家庭支出增加了14%。
8.7.1 时间上的效果异质性(Heterogeneous Effect over Time)
有好消息也有坏消息。首先,好消息是:你已经识别出了问题,即你知道将TWFE应用于具有时间效果异质的交错采纳数据时,会产生偏差。从更专业的角度来看,你的数据生成过程具有不同的效果参数:
Y i t = τ i t W i t + α i + γ t + e i t Y_{it}=\tau_{it} W_{it} +\alpha_i +\gamma_t +e_{it} Yit=τitWit+αi+γt+eit
但你假设效果是恒定的:
Y i t = τ W i t + α i + γ t + e i t Y_{it}=\tau W_{it} +\alpha_i +\gamma_t +e_{it} Yit=τWit+αi+γt+eit
如果这就是问题所在,一个简单的解决方法是允许每个时间和单元有不同的效应。理论上,你可以通过以下公式来实现这一点:
downloads ~ treated:post:C(date):C(city) + C(date) + C(city)
这样就解决了问题吗?嗯,不完全是。现在是坏消息:这个模型的参数会比数据点还多。由于你要考虑日期和单元的交互,每个单元在每个时间段都会有一个干预效果参数。但这正是你所拥有的样本数量!OLS甚至无法在此运行。
所以你需要减少模型的干预效果参数的数量。为了实现这一点,你能想到一种将单元分组的方法吗?如果你稍加思考,你会看到一个非常自然的方式来对单元分组:按群组分组!你知道整个群组中的效果随时间变化遵循相同的模式。因此,对这个不切实际的模型的一个自然改进是允许效果按群组变化,而不是按单元变化:
Y i t = τ g t W i t + α i + γ t + e i t Y_{it}=\tau_{gt} W_{it} +\alpha_i +\gamma_t +e_{it} Yit=τgtWit+αi+γt+eit
这个模型的干预效果参数的数量更合理,因为群组的数量通常远小于单元的数量。现在,你终于可以运行模型了:
formula = "downloads ~ treated:post:C(cohort):C(date) + C(city)+C(date)"
twfe_model = smf.ols(formula, data=mkt_data_cohorts_w).fit()
这将为你提供多个ATT估算值:每个群组和日期都有一个。所以,为了验证你是否正确,你可以计算模型隐含的个体干预效果估计值,并平均结果。为此,只需将干预后周期受干预单元的实际结果与模型预测的 y ^ 0 \hat y_0 y^0 进行比较:
df_pred = (
mkt_data_cohorts_w
.query("post==1 & treated==1")
.assign(y_hat_0=lambda d: twfe_model.predict(d.assign(treated=0)))
.assign(effect_hat=lambda d: d["downloads"] - d["y_hat_0"])
)
print("Number of param.:", len(twfe_model.params))
print("True Effect: ", df_pred["tau"].mean())
print("Pred. Effect: ", df_pred["effect_hat"].mean())
Number of param.: 510
True Effect: 2.2625252108176266
Pred. Effect: 2.259766144685074
终于!这得到了一个带有许多参数(510个!)的模型,但它确实设法恢复了真实的ATT。你甚至可以提取这些ATT并绘制它们:
formula = "downloads ~ treated:post:C(cohort):C(date) + C(city) + C(date)"
twfe_model = smf.ols(formula, data=mkt_data_cohorts_w.astype({"date":str, "cohort": str})).fit()
effects = (twfe_model.params[twfe_model.params.index.str.contains("treated")]
.reset_index()
.rename(columns={0:"param"})
.assign(cohort=lambda d: d["index"].str.extract(r'C\(cohort\)\[(.*)\]:'))
.assign(date=lambda d: d["index"].str.extract(r':C\(date\)\[(.*)\]'))
.assign(date=lambda d: pd.to_datetime(d["date"]), cohort=lambda d: pd.to_datetime(d["cohort"])))
plt.figure(figsize=(10,4))
sns.lineplot(data=effects, x="date", y="param", hue="cohort", palette="gray")
plt.xticks(rotation=45)
plt.ylabel("Estimated Effect")
plt.legend(fontsize=12)
这个图表的优点在于,它与你的效果应该如何表现的直觉相符:它逐渐上升,并在一段时间后保持恒定。此外,它向你展示了对于所有干预前周期以及从未受干预的群组,效应为零。这可能给了你一些如何减少这个模型参数数量的想法。例如,你可以只考虑大于群组的周期的效果:
Y i t = τ g , t ≥ g W i t + α i + γ t + e i t Y_{it}=\tau_{g,t≥g} W_{it} +\alpha_i +\gamma_t +e_{it} Yit=τg,t≥gWit+αi+γt+eit
不过,这将涉及非凡数量的特征工程,因为你必须在干预之前对日期进行分组,但你也知道这可能是很好的做法。
另请参阅
解决干预效果异质性问题的这个方案受到了Sun和Abraham的论文《在存在异质干预效果的事件研究中估算动态干预效果》(Estimating Dynamic Treatment Effects in Event Studies with Heterogeneous Treatment Effects)以及Jeffrey Wooldridge的论文《双向固定效应、双向Mundlak回归以及双重差分估计量》(Two-Way Fixed Effects, the Two-Way Mundlak Regression, and Difference-in-Differences Estimators)的启发。
就像你在解决将协变量纳入双重差分模型的问题时一样,这种双向固定效应偏差也有两种解决方案。你刚刚看到的那种方法在运行双向固定效应模型时,巧妙地结合了虚拟变量。另一种方法则是将问题分解成多个2×2的双重差分,单独解决每一个,然后再将结果组合起来。其中一种做法是为每个群组估算一个双重差分模型,使用从未受干预的群组作为对照组:
cohorts = sorted(mkt_data_cohorts_w["cohort"].unique())
treated_G = cohorts[:-1]
nvr_treated = cohorts[-1]
def did_g_vs_nvr_treated(df: pd.DataFrame,
cohort: str,
nvr_treated: str,
cohort_col: str = "cohort",
date_col: str = "date",
y_col: str = "downloads"):
did_g = (
df
.loc[lambda d:(d[cohort_col] == cohort)|
(d[cohort_col] == nvr_treated)]
.assign(treated = lambda d: (d[cohort_col] == cohort)*1)
.assign(post = lambda d:(pd.to_datetime(d[date_col])>=cohort)*1)
)
att_g = smf.ols(f"{y_col} ~ treated*post",
data=did_g).fit().params["treated:post"]
size = len(did_g.query("treated==1 & post==1"))
return {"att_g": att_g, "size": size}
atts = pd.DataFrame(
[did_g_vs_nvr_treated(mkt_data_cohorts_w, cohort, nvr_treated)
for cohort in treated_G]
)
atts
| att_g | size | |
|---|---|---|
| 0 | 3.455535 | 702 |
| 1 | 1.659068 | 1044 |
| 2 | 1.573687 | 420 |
然后,你可以使用加权平均数将结果与每个群组的样本量( T ∗ N T*N T∗N)结合起来。所得估算值与你之前估算的值非常相似:
(atts["att_g"]*atts["size"]).sum()/atts["size"].sum()
2.2247467740558697
或者,除了使用从未受干预的群组作为对照外,你还可以使用尚未受干预的群组,这会增加对照组的样本量。这有点麻烦,因为你必须为同一群组多次运行双重差分。
另请参阅
解决效果异质性问题的第二种方案受到了Pedro H. C. Sant’Anna和Brantly Callaway的论文《多周期的双重差分法》(Difference-in-Differences with Multiple Time Periods)的启发。在论文中,他们还介绍了如何将尚未干预群组的作为对照组,以及如何使用双重鲁棒的双重差分法。
8.7.2 协变量(Covariates)
在处理了TWFE偏差问题之后,剩下的就是如何使用整个数据集、所有时间段、交错采纳设计以及所有区间,这将需要在模型中包含协变量。
幸运的是,这里并没有什么特别新的内容。所要做的就是记住之前如何将协变量添加到双重差分模型中。在这种情况下,需要将协变量与干预后虚拟变量进行交互。而在这里,与干预后的虚拟变量相似的是日期列,它标记着时间的流逝。因此,所要做的就是将协变量与该列进行交互:
formula = """
downloads ~ treated:post:C(cohort):C(date)
+ C(date):C(region) + C(city) + C(date)"""
twfe_model = smf.ols(formula, data=mkt_data_cohorts).fit()
再次提醒,由于这个模型将提供一堆参数估算值,你可以通过计算个体效果并平均来获得ATT:
df_pred = (
mkt_data_cohorts
.query("post==1 & treated==1")
.assign(y_hat_0=lambda d: twfe_model.predict(d.assign(treated=0)))
.assign(effect_hat=lambda d: d["downloads"] - d["y_hat_0"])
)
print("Number of param.:", len(twfe_model.params))
print("True Effect: ", df_pred["tau"].mean())
print("Pred. Effect: ", df_pred["effect_hat"].mean())
Number of param.: 935
True Effect: 2.078397729895905
Pred. Effect: 2.0426262863584568
如果你选择将交错采纳分解为多个2×2块,还可以在每个DID模型中单独添加协变量,就像之前所做的那样。
8.8 要点总结
面板数据方法是因果推断中一个令人兴奋且快速发展的领域。其带来的许多承诺都源于一个事实,即拥有额外的时间维度不仅可以让你从对照单元中估算受干预组的反事实,还可以从受干预组的过去中估算。
在本章中,你已经探索了应用双重差分的多种方法。双重差分放宽了传统的无混淆假设( T d ⊥ T ∣ X T_d \perp T|X Td⊥T∣X),将其转变为条件平行假设:
Δ T d ⊥ T ∣ X \Delta T_d \perp T|X ΔTd⊥T∣X
如果你有不可观测的混淆因子,这给了你一些希望。对于面板数据,只要那些混淆因子在同一单元内随时间保持不变,或在同一时间段内随单元保持不变,你仍然可以识别ATT。
尽管双重差分具有很大的威力,但它也并非没有复杂性。如果你超越了规范的双重差分公式,你就需要非常小心地建模。虽然2 × 2的双重差分具有非参数模型的灵活性,但更一般的交错采纳设置就无法这么说,因为它需要你做出额外的功能形式假设。
本章教你如何处理简单2 × 2情况之外的许多扩展,包括添加协变量、估算效果随时间的变化,以及允许不同的干预时间。然而,请记住,所有这一切都是非常新的,如果这个领域在不久的将来超越了现有的内容,我也不会感到惊讶。不过,本章应该为你提供了一个相当坚实的基础,以便在必要时迅速赶上。
系列文章专栏:
使用Python进行因果推断(Causal Inference in Python)
第1章 因果推断导论
第2章 随机实验与统计学回顾
第3章 图形化因果模型
第4章 线性回归的不合理有效性
第5章 倾向分
第6章 效果异质性
第7章 元学习器
第8章 双重差分
持续更新中:
第9章 综合控制
第10章 Geo实验与Switchback实验
第11章 不依从性与工具
第12章 后续行动
【参考】
原版书籍《Causal Inference in Python: Applying Causal Inference in the Tech Industry》
原书github代码