计算机视觉深度学习入门笔记-从理论到实战案例

第一章 深度学习概论

深度学习是一种机器学习的分支，致力于模拟人脑神经网络的工作原理。通过构建具有多层次结构的神经网络模型，深度学习可以从大量数据中学习和提取特征，以解决各种复杂的任务。在过去的几年中，AI在各个领域都有突飞猛进的发展。就如同追求物理学中大统一，对于各式的AI模型，人们希望建立一个统一的通用人工智能（AGI）。在自然语言模型中，ChatGPT或许已经具有在部分领域AGI的雏形，尽管其仍然存在很多问题，对于某些交互存在胡言乱语的情况。但不可否认的是，我们或许能够在有生之年见证真正的AGI的诞生。对于CV领域我们也需要一个AGI雏形，而深度学习是AI领域的根本，更加需要我们深入的理解与学习。

1.1神经网络基础

在学习深度学习之前我一直很好奇，为什么是神经网络？ 为什么神经网络有效？如何训练神经网络？要回答这些问题我们需要回到深度学习，或者说数学模型的目的。数学模型的目的是通过使用数学语言和符号来描述和表示现实世界中的某种问题或系统。它可以帮助我们理解问题的本质、预测行为和探索潜在的解决方案。

1.1.1为什么是神经网络？

我能想到的接触到第一个数学模型，就是一元回归问题。我们利用已用的自变量与因变量的关系，预测未知自变量对应的因变量值。该关系可表示为：

Y = β0 + β1*X + ε
其中β0和β1是回归系数。ε是误差项，用于表示模型无法完全解释的随机误差，一般不考虑。在中学我们学习了如何求解β0和β1是回归系数的方法— 最小二乘法。
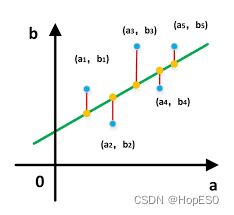
最小二乘法的数学表达式我们已经耳熟能详，这里不再赘述。总之我们通过这种方法，实现了一个单一变量的数学预测模型。而实际上神经网络与这种数学方法有异曲同工之妙，现在回过头看神经网络的结构。
对于输入层的三个输入x1，x2，x3。我们可以理解为三个自变量，他们同时连接了隐藏层中的四个节点， $a^{[0]}$为输入矩阵。
a [ 0 ] = [ x 1 x 2 x 3 ] a^{[0]}=\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\end{bmatrix} a[0]= ​x1​x2​x3​​ ​

以第一个节点$a_1^{[1]}$为例,在该节点中进行一次线性运算。

$z_1^{[1]}=w_1^{[1]}{a}^{[0]}+b_1^{[1]}$
$a_1^{[1]}=\sigma (z_1^{[1]})$

其中[*]表示层数，输入层为第0层，脚标表示层中的顺序。这里进行的是矩阵运算，其中$w_1^{[1]}$为[1,3]的权重矩阵，$b_1^{[1]}$为偏执项。$\sigma (x)$为激活函数，有多种选择，它们为神经元引入了非线性特性，并允许神经网络能够学习和处理更加复杂的数据，对于不同的模型或者层，激活函数选择也会极大的影响模型性能，在示例中，我选择了sigmiod函数。

$\sigma (x)=\frac{1}{1+e^{-x}}$

对于$z_1^{[1]}$的计算在形式上与一元回归的数学公式高度相似，但实际上并不是单一变量的运算，有线性代数的知识不难计算$z_1^{[1]}，\sigma (z_1^{[1]})$，对于这样的一个节点我们称其为一个神经元，每个神经元都执行相同的操作。同理求解同层其他神经元的输出，第一个隐藏层的输出$a^{[1]}$，也就是$\sigma (z^{[1]})$为[4,1]的矩阵。上一层的输出将做为下一层的输入，于是矩阵的维度会随着层中神经元的个数而变换，在后续会提到这个变换实际上可以加深数据深度。多个神经元构成一个隐藏层，多个隐藏层构成一个网络，这个不断向下层传播的过程我们称之为前向传播。那么为什么需要这么多神经元以及层呢？实际上，如果只有一个神经元，这个数学模型只能解决线性问题，因为对于单个神经元就是进行线性运算。为了更好解决非线性问题，更多更深的网络也随之出现，随着网络复杂化，模型转而进行着非线性运算。 当然激活函数加入也使得网络具有非线性，二者共同作用可以是模型具有更好的泛性。

1.1.2为什么神经网络有效？

在一元线性回归中，我们之所以能够预测数据走势，除了模型建立，另外最重要的就是β0和β1是回归系数的求解。通过最小二乘法，可以求解回归系数，那么为什么是最小二乘法？ 最小二乘法为什么有效？
最小二乘法的目标是使得观测值与模型预测值之间的残差（实际观测值与模型预测值之间的差异）的平方和最小化。通过最小化残差平方和，可以找到在给定模型下使预测误差最小的参数，并得到对观测数据的最佳拟合。
数学上，使用最小二乘法拟合线性回归模型时，使用导数来推导出最小二乘估计的具体表达式。将残差平方和作为目标函数，对回归系数进行求导并令导数等于零，可以得到一组正规方程，从而求解出最优的回归系数。导数在最小二乘法中的作用是确定目标函数的极值点，而在这里我们寻求的是目标函数的最小值。求取导数并令其为零的过程涉及到对目标函数的求导操作，通过对导数的分析和求解，我们能够找到使目标函数最小化的参数值。
同样在神经元中求解$w_1^{[1]}$ ,$b_1^{[1]}$也是基于类似的思想。首先我们需要定义观测值与模型预测值之间的损失函数，在这里我们可以有多个选择，在解决不同的问题时我们也会考虑不同损失函数。例如：L1损失函数，L2损失函数。在这里我以交叉熵损失函数为例，假设预测目标只有一个，即模型最终输出只有一个$\hat{y}$值,$y$为对应的观测值，且为0，1问题。其数学表达式为：

$l(y,\hat{y})=-(yln(\hat{y})+(1-y)ln(1-\hat{y}))$

那么这个函数为什么具有判断观测值与模型预测值之间的误差的能力呢？实际上不能看出$\hat{y}=1$时，$y$如果为1，$l(y,\hat{y})=0$，这表示$\hat{y}$趋近于$y$，相反$y$如果为0，$l(y,\hat{y})=+\infty$，表示误差无限大。同理$\hat{y}=1$时也有对应的结果。所以该函数与方差型损失函数都具有相同的效果，在数学上称之为拉斐尔效应。在这个问题中$l(y,\hat{y})\in (0,+\infty )$，且$l(y,\hat{y})$越大，$\hat{y}$是$y$的估计的概率越小。同时不能看出该函数是凸函数，有全局最优解，故该函数适合单一优化示例的情况。
接下我们需要利用高数的知识求使$l(y,\hat{y})$最小的$w$ ,$b$。这里我以单个神经元，输入为两个变量的模型，激活函数与损失函数不变为例，详细展示其求解过程。设：

$x={\left[\begin{array}{cc}{x}_1& x_2\end{array}\right]}^T$， $w=\left[\begin{array}{cc}{w}_1& w_2\end{array}\right]，b$

那么整个网络的正向传播数学表达可以写为：

$z=x_1{w}_1+x_2{w}_2+b⟶\hat{y}=\sigma (z)⟶l(\hat{y},y)$

利用链式法则反向求导：

$\frac{\partial l(\hat{y},y)}{\partial \hat{y}}=-\frac{y}{\hat{y}}+\frac{1-y}{1-\hat{y}}$
$\frac{\partial l(\hat{y},y)}{\partial z}=\frac{\partial l(\hat{y},y)}{\partial \hat{y}}\frac{\partial \hat{y}}{\partial z}=(-\frac{y}{\hat{y}}+\frac{1-y}{1-\hat{y}})(\hat{y}(1-\hat{y}))=\hat{y}-y$
$\frac{\partial l(\hat{y},y)}{\partial w_1}=\frac{\partial l(\hat{y},y)}{\partial \hat{y}}\frac{\partial \hat{y}}{\partial z}\frac{\partial z}{\partial w_1}=(\hat{y}-y)x_1$
$\frac{\partial l(\hat{y},y)}{\partial w_2}=\frac{\partial l(\hat{y},y)}{\partial \hat{y}}\frac{\partial \hat{y}}{\partial z}\frac{\partial z}{\partial w_2}=(\hat{y}-y)x_2$
$\frac{\partial l(\hat{y},y)}{\partial b}=\frac{\partial l(\hat{y},y)}{\partial \hat{y}}\frac{\partial \hat{y}}{\partial z}\frac{\partial z}{\partial b}=\hat{y}-y$

利用得到的导数我们可以不断更新$w=\left[\begin{array}{cc}{w}_1& w_2\end{array}\right]，b$。

$\{\begin{array}{l}{w}_1=w_1-\alpha \frac{\partial l}{\partial w_1}\\ w_2=w_2-\alpha \frac{\partial l}{\partial w_2}\\ b=b-\alpha \frac{\partial l}{\partial b}\end{array}$

那么我们可以利用迭代的方式，先给$w=\left[\begin{array}{cc}{w}_1& w_2\end{array}\right]，b$赋值，在不断通过求导迭代，逼近最优解，其中$\alpha$即为学习率。这个过程就称之为反向传播，总结来说反向传播通过计算损失函数对网络中每个参数的梯度，并将这些梯度信息沿着网络向后传播，以便根据梯度更新参数。并且在反向传播的过程我们也不难发现激活函数另一个作用就是传递梯度，不同激活函数的选择，也会影响学习效率，甚至会引起梯度消失以及梯度爆炸等一系列问题。

1.1.3神经网络的运行

单个神经元中所包含的数学逻辑是较为简单，我们也可以直接使用数学推导求解每一次迭代的结果。但神经网络往往是十分复杂的，这也就代表着需要计算更新的参数往往是海量的。所以对于较大的模型我们或许无需拘泥某一个参数的迭代过程，计算机的出现就可以帮助我们解决这一系列问题。我们更需要将注意力放在模型的运行过程上，也就是模型结构上。借助吴恩达教授给出的示意图，接下来我们就对于$l$层的神经网络进行分析，了解其具体的运行过程。
在模型中，从输入到输出的过程称之为前向传播，也就是绿色的框所示的过程，每个层中都有待确定的参数。我们通过损失函数基于链式法制求导，利用参数的梯度修正待确定参数，使得损失函数最小。这个过程就是反向传播，在图中表示为红色框所示。通过这张图可以清晰的了解神经网络的运行过程，我们要做的事情就是利用编译器，将这个过程实现。当然这里还有许多细节需要我们注意，比如设置多少层神经网络？每层中需要多少个神经元？损失函数与激活函数如何选择？还有一些数据处理和结果展示上细节需要我们深究，这部分我将统一放到第二章讲解。

1.2卷积神经网络

1.2.1图像——矩阵

数字图像
一张彩色图像是由同维的红、绿、蓝三张单色图构成。在数字图像处理中可以使用一个矩阵表示一个单色图，矩阵中数字表示对应像素点亮度，以下是单通道数字图像矩阵的示例。

在计算机中这个矩阵对应了左上角和右下角有色彩的图像的单个通道的数据。在本课题中所拍摄图像均为彩色图，包含了三个单色矩阵。但在实际处理中，由于背光板的曝光，图像只有黑白两色，多余色彩信息会增加无意义的计算量。所以本课题中图像处理方案所涉及的算法都是基于像素点的灰度值来进行处理的。
灰度图
灰度图是一种在计算机上呈现图像的方式，它将彩色图像转换为失去色彩信息的图像，只保留一张单色灰度图，灰度图中的每个像素点都有一个灰度值，通常在0到255的范围内，表示该像素的亮度程度。此外，灰度图在很多图像处理领域都有广泛的应用，例如图像增强、边缘检测、图像分割等。由于灰度图仅包含亮度信息，因此其文件大小相对于彩色图像更小，处理速度更快，也更容易进行数学运算和分析。
二值图
二值图是一种仅包含黑白两种颜色的图像，其中黑色表示0，白色表示1。二值图通常用于图像处理、计算机视觉等领域，以提取物体的轮廓、边缘、形状等特征。以下将从应用和优缺点两方面进行更为详细的描述。此外，在图像的压缩和储存过程中，也常使用二值化的方法，可以大大降低图像的储存空间，提高处理效率。在计算机视觉领域中，二值图被广泛应用于目标检测、识别等任务。例如，在人脸识别中，可以将一张彩色人脸图像转换为二值图，并利用二值图像的轮廓等特征来识别人脸。在文本识别领域中，也可以将一张图像转换为二值图，以便于提取文字等特征。在数字识别中，二值图也是常用的处理方式。对于手写数字，可以通过将数字图像二值化，提取出数字的轮廓特征，并将其与已有的数字模板进行比对，以识别手写数字。

1.2.2为什么是卷积？

在信号与系统中我们学习到信号通过线性系统的过程可以使用卷积来表示。从数学上分析，卷积是一种在两个函数（或信号）之间进行操作的运算。它通过将一个函数与另一个函数的翻转和平移进行加权相乘并求和，可以得到一个新的函数。而图像就是一种信号，经过一个卷积神经元可以近似认为经过一个线性系统。从物理意义上分析，卷积神经网络之所以采用卷积操作，是因为卷积具有局部感知、参数共享、尺度不变性和特征的组合等特性，使得它成为处理图像和模式识别任务的强大工具。

在这个示例中展示了，图像的卷积运算的实现过程。Sobel算子是一个3x3的卷积核，对应的神经网络中的一个神经元权重$w$,在图像上采集一个与卷积核大小相等的视窗，对应位置相乘再求和，就得到了输出矩阵中的一个元素的值。如红色视窗在通过卷积核的输出就是红色的元素，视窗的位置是按照一定步长移动的，这里步长为1，遍历图像上所有视窗可能存在的位置就得到了输出。这就是卷积神经网络的前向传播，并且我们观察结果不难发现，通过卷积的运算，我们也很好的提取了图像边缘信息，这恰好能体现卷积的物理意义。对于输出我们发现图像长宽发生了变化，如果你想让输出维度等于输入维度话，可以使用填充操作。并且卷积层有几个卷积核我们就能得到多少个输出，将这些图片堆叠在一起就形成了高通道数的图片。实际上卷积层实现的就是通过不断的特征提取，减少图像长宽，增加图片的深度信息也就是通道数。

1.2.3卷积神经网络的传播

上一小节中我们引入卷积核的概念，卷积神经网络中的反向传播即为更新卷积核中的权重。相较于多层感知机中的权重更新需要更加丰富的数学知识。有兴趣的朋友可以参考链接卷积神经网络的反向传播，里面有更加详细的数学推导过程。
另外，区别于多层感知机的是，在卷积网络的模型设置时，我们需要考虑更多的因素。比如卷积核的步长，卷积核的大小，填充，池化等问题。并且部分卷积神经网络在多个卷积层后会补充全连接层。所以接下来我将从VGG模型中详细分析搭建训练卷积神经网络的过程。

1.3VGG模型——传统串行网路的大成之作

VGG是一种深度卷积神经网络模型，由牛津大学的研究团队于2014年提出（Very Deep Convolutional Networks for Large-Scale Visual Recognition）。它在ImageNet图像分类挑战赛中取得了优异的表现，是传统串行网络的集大成之作，成为深度学习发展历程中的重要里程碑。有兴趣的朋友也可以去阅读原论文。

1.3.1网络结构

图片中展示的是VGG16与VGG19两个VGG模型分支的网络结构，接下来我将以VGG16为案例分析其网络结构。作者将VGG16模型分成了5个block。如下D所示。
结合这两张图片，以block1为例，包含两个相同结构的卷积层，卷积核大小为3x3，步长为1，卷积核也就是层中神经元的个数为64。每个block结束后都添加了Max pooling（最大池化）层是卷积神经网络中常用的一种池化操作。它的主要作用是在减小特征图的空间尺寸的同时保留重要的特征信息。具体而言，max pooling层对于输入的特征图划分为不重叠的子区域（一般是2x2或3x3的窗口），然后在每个子区域内选择最大值作为输出。这样就将原始特征图压缩，并保留了最显著的特征元素，也可以称之为下采样。在图一中我们也可以发现经过池化层以后，图片的维度减半，说明在模型选择了2x2视窗作为子区域，进行了采样与降维。在经过了五个block后，模型添加了3个全连接层，这是为了在卷积层提取到的高级抽象特征基础上进行分类和预测。全连接层是由多个神经元（节点）组成的层，我们之前提到其中每个神经元与前一层的所有神经元相连接。在VGG16模型中，全连接层通常用于将卷积层提取到的特征映射转化为具体的类别或标签预测。具体来说，全连接层在VGG16的末尾接受扁平化操作（将图片展开为一维向量）后的特征向量作为输入，并将其传递给多个全连接层，用于执行分类任务。这些全连接层通过学习权重参数，将高级抽象特征与类别的概率分布相关联，从而实现对输入图像的分类。

1.3.2运行过程

可以参考图一，输入224x224x3图像。进入卷积层之前进行0填充，在输入图片外加一圈0像素值点，这样可以保证输出维度等于输入维度。输入图像经过一系列的卷积层和非线性激活函数（通常使用ReLU）进行特征提取。通过不断堆叠卷积层和池化层，VGG16模型逐渐提取出输入图像中的抽象特征映射。随着网络的深度增加，特征映射的空间尺寸缩小，但特征的通道数（表示不同的特征）增加。 以第一个block为例，经过第一个block和池化层，最终图片的长宽减半但是特征通道数增加到卷积核的个数64层，这时的图片具有更加丰富的特征信息。最后一个池化层输出7x7x512的图片，将扁平化后的特征向量传递给全连接层。这些全连接层通过学习权重参数，将高级抽象特征与类别的概率分布相关联，实现对输入图像的分类预测。最后一个全连接层的输出经过softmax函数，将输出转化为在各个类别上的概率分布。最大概率所对应的类别即为VGG16对输入图像的分类结果。
总体而言，VGG16通过卷积层逐渐提取输入图像的特征映射，并通过全连接层将这些特征映射转化为类别的预测概率。它实现了从低层次的图像信息（如边缘、纹理）到高层次的语义特征（如对象类别）的自动学习与特征提取。

1.3.3模型的优化

VGG16在图像分类问题上具有十分卓越的性能，但也有两个问题值得我们思考与深究。第一，VGG16对图片的输入有严格的要求，必须是224x224的图片，对于不满足条件图片我们只能采用放缩或者裁剪的方式进行预处理。第二，VGG16总共需要拟合138M个参数，而在第一个全连接中输入为1x1x25088（7x7x512），输出为4096，那么这一层就有102M（25088x4096）个参数，这无疑极大影响了模型学习速度。针对这些问题后续的学者也提出一些解决方案。
对于第一个问题，我们可以将全连接层修改成卷积层，构造1x1的卷积核代替全连接层，可以在一定程度上缓解VGG16模型对输入图像尺寸的限制。这种修改被称为 “全卷积化”（Fully Convolutional）或"卷积分类器"（Convolutional Classifier）。 传统的全连接层可以看作是一个N个神经元组成的一维向量与特征图进行矩阵乘法操作，但使用1x1卷积核的卷积层在操作上等效于点乘。因此，通过使用1x1卷积层来替代全连接层，可以将空间维度保留在特征映射中，避免了输入图像尺寸严格要求的限制。 这种修改对于在不同尺寸的输入图像上运行模型时尤为有用，它使得模型可以接受任意尺寸的输入，并输出相应尺寸的特征图。这也为涉及对象检测、语义分割等任务提供了便利，因为这些任务通常需要获取完整的特征图以产生密集的预测结果。通过将全连接层改为1x1卷积层，可以减少模型中的参数数量，并提高模型的计算效率。此外，该修改通常还可以提供更好的特征表示能力和泛化性能，因为卷积层可以利用空间上的局部信息进行特征选择和组合。
对于第二个问题，也有学者建议使用全局平均池化代替全连接层。传统的深度学习模型（包括VGG16）通常在最后一层使用全连接层作为分类器。然而，后续的研究表明，可以用全局平均池化（Global Average Pooling）代替全连接层，以减少参数数量和计算量。全局平均池化将特征图的每个通道上的特征进行平均，然后直接用这些平均值作为输出类别的得分。这种方法消除了全连接层中大量参数的需求，并且提供更好的泛化性能和更快的训练速度。

第二章 神经网络的训练

2.1pytorch与面向对象

PyTorch是一个基于Python的科学计算库，被广泛用于构建深度神经网络和其他机器学习模型。它提供了张量操作、自动微分、优化算法等功能，并提供了易用性和高效性。PyTorch的核心是张量（Tensor），它是多维数组的扩展形式。PyTorch提供了强大的张量操作工具，包括矩阵计算、向量运算、广播操作等。开发人员可以使用这些操作来处理不同类型和维度的数据，并在CPU或GPU上高效执行计算。在神经网络的训练中，自动微分（Autograd）是一项重要技术。PyTorch通过其自动微分引擎，可以自动计算变量的导数，并支持高效的反向传播算法。这使得开发人员能够轻松地定义和训练复杂的神经网络模型。此外，PyTorch包含了一个强大的神经网络库，可以用来构建各种深度神经网络架构。它提供了全连接层、卷积层、循环神经网络（RNN）等常用模块，同时也支持各种激活函数和损失函数。
面向对象是搭建神经网络中常用的一种方式，由于pytorch中torch.nn.Module库集成多种网络层的结构，利用类的继承搭建神经网络是很方便的方法。这里也附上pytorch的官网，里面有所有可能用得到的函数的介绍，也有一些搭建好的网络结构比如VGG16可以直接“CV”

#利用pytorch搭建100个神经元的神经网络
class Net(torch.nn.Module):
    def __init__(self,n_feature,n_output):
        super(Net,self).__init__()#继承父类torch.nn.Module中的属性创建网络
        self.hidden=torch.nn.Linear(n_feature,100)
        self.predict=torch.nn.Linear(100,n_output)

2.2数据预处理与传播方式的选择

2.2.1小批量梯度下降算法

在实应用中，为了保证模型的泛型和准确度，对于数据预处理是很重要的。比如样本过少我们可以通过反转，色域扭曲（加上一些特定范围内随机的滤波器）得到更加丰富的样本。另外，对样本进行一些特殊操作也有利于模型的搭建，比如，归一化处理，将样本进行标准化处理。在输入过程中，我们通常会因为硬件算力不够，无法一次性处理整个样本集，而需要使用小批量梯度下降（Mini-Batch Gradient Descent进行优化。小批量梯度下降是一种梯度下降算法的变体，在深度学习中广泛应用于训练神经网络。它通过更新模型参数来最小化损失函数，并且每次优化不会使用单个样本（随机梯度下降），也不使用全部样本（批量梯度下降），而是利用一个小批量样本来进行优化。给定一个损失函数L，目标是找到使L最小化的模型参数w。小批量梯度下降的迭代步骤如下：
分割训练数据集为大小为m的小批量样本：$(x^i,y^i)$,$i$样本中的索引。
计算当前批量样本的平均损失函数值：$\hat{L}=\frac{1}{m}{\sum }_{i=1}^{m}L(y^i,{\hat{y}}^i)$
根据损失函数对参数求导数，计算批量样本的梯度：${\nabla }_w\hat{L}$
更新模型参数:$w=w-\alpha {\nabla }_w\hat{L}$
除此之外，小批量梯度下降算法还有以下优势
更快的收敛速度： 与随机梯度下降相比，小批量梯度下降可以更稳定地接近最优解。通过使用多个样本进行参数更新，可以减少参数更新的方差，从而加快收敛速度。
更高的内存效率： 相对于批量梯度下降，在每次参数更新时，小批量梯度下降只需加载和处理一个小批量的数据。这对于大规模数据集来说更加内存高效，并且在GPU上并行计算时，小批量操作可以更好地利用硬件资源。
更好的泛化性能：与随机梯度下降相比，小批量梯度下降通常可以提供更好的泛化性能。通过同时考虑多个样本，模型参数可以更好地调整以适应整个训练数据集的分布，而不仅仅是单个样本的特征。

2.2.2指数加权平均

指数加权平均（Exponential Weighted Average）是一种用于平滑时间序列数据的方法。它通过对过去观测值进行加权平均，使较新的观测值得到更大的权重，而较早的观测值权重逐渐减小。
给定一个时间序列$(x_1,x_2,\dots ,x_t)$，其中 $x_i$ 表示第i个观测值，指数加权平均可以通过以下方式计算：

$V_t=(1-\beta )\cdot V_{t-1}+\beta \cdot x_t$

其中， $V_t$ 表示在时刻 $t$ 的指数加权平均值， $\beta$ 是一个在0和1之间的常数，用于控制权重的衰减速度。值得注意的是，可以选择对初始值$V_0$进行设定或者将其设置为$x_1$。这样做的好处是使得输入数据有权重衰减特性，较新观测值的权重较大，较早观测值的权重逐渐减小。 $\beta$ 的取值决定了衰减的速度。较大的$\beta$ 值意味着较快的衰减，反之亦然。因此指数加权平均常用于时间序列数据的平滑处理，例如预测问题中的走势分析、季节性调整等。它可以去除噪声、抹平波动，并提供一个更平稳的信号，从而帮助识别出数据中的趋势和模式。此外，指数加权平均在一些优化算法（如Adam优化器）中也被广泛应用，用于计算参数更新过程中的移动平均梯度值。

2.2.3均方根传递

均方根传递（Root Mean Square Propagation，RMSprop）是一种用于优化神经网络的梯度下降算法之一。它是由Tieleman和Hinton在2012年提出的，并在训练深度学习模型时非常有效。例如学习率选择困难、陷入局部最小值等。它通过针对不同梯度信息的变化情况来自适应地调整学习率，从而加快收敛速度以及帮助模型跳出局部极小点。RMSprop使用了指数加权平均的方法来更新梯度。具体而言，它计算过去一段时间内梯度的平方的移动平均值（也称为二次梯度平均值）。然后，将当前的梯度除以这个平均值的平方根，来缩放学习率。RMSprop的更新步骤可以表示为以下公式：
计算梯度的平方与参数 v 的衰减平均值，可使用指数加权平均方法:

$v=\beta \cdot v+(1-\beta )\cdot {\text{gradient}}^2$

更新参数：
$$\text{parameter}=\text{parameter}-\alpha \cdot \frac{\text{gradient}}{\sqrt{v+ϵ}}$$
这里 $ϵ$是为了防止除零错误而添加的小常数。gradient：梯度，指示了目标函数关于参数的斜率（导数）。在每次迭代中，通过反向传播计算得到的梯度用于更新参数。parameter：参数，需要优化的模型参数。通过梯度下降算法进行更新，以最小化损失函数。通过在更新过程中使用衰减平均值来调整学习率，RMSprop能够自适应地缩放每个参数的梯度。因此，在距离最优解较远时，RMSprop能够提供快速收敛；而在接近最优解时，它可以减小学习速率，以避免超调。

2.2.4适应性矩阵估计

综合上述几个算法，适应性矩阵估计（Adaptive Moment Estimation，Adam）是一种用于优化神经网络的梯度下降算法之一。Adam算法使用指数加权平均的方法来自适应地更新不同参数的梯度。它具有两个主要步骤：第一步是一个动量估计，类似于Momentum算法；第二步是一个自适应学习率估计，类似于RMSprop算法。以下是Adam算法的更新步骤：
首先初始化参数$m$和$v$为0作为初始项。这些参数分别对应动量估计和适应学习率估计。
在每一次迭代中，计算梯度并更新参数：
计算梯度的一阶矩估计（mean）：$$m={\beta }_1\cdot m+(1-{\beta }_1)\cdot \text{gradient}$$
计算梯度的二阶矩估计（variance）：$$v={\beta }_2\cdot v+(1-{\beta }_2)\cdot ({\text{gradient}}^2)$$
这里，${\beta }_1$,${\beta }_2$是衰减率（即动量估计和二阶矩估计的衰减因子），通常设置为0.9和0.999。
使用偏差修正（bias correction）： $$m_{\text{corrected}}=\frac{m}{1-{\beta }_1^t}$$和$$v_{\text{corrected}}=\frac{v}{1-{\beta }_2^t}$$
其中，t 是当前迭代步骤的次数。
更新参数：$$\text{parameter}=\text{parameter}-\alpha \cdot \frac{m_{\text{corrected}}}{\sqrt{v_{\text{corrected}}}+ϵ}$$
同样这里 ϵ 是为了防止除零错误而添加的小常数。由于ADM算法的优越性，在后续的案例实战中将统一使用ADM做为模型的优化算法。

2.3激活函数与损失函数的选择

2.3.1 激活函数

之前我们提到选择非线性激活函数的原因是线性函数的输入与输出只是简单的放缩或者偏移，没有足够的泛型与适应能力。非线性函数有助于减少梯度消失的问题，是模型更加稳定和鲁棒。在这里介绍三种常见的非线性激活函数，以及它们的使用场景。
Relu函数： 数学表达式为$f(x)=\max (0,x)$，Relu函数将负数映射为零，而对于非负数保持不变。显然其具计算简单、梯度不会饱和（在正区间上恒等于1），有效地解决了梯度消失问题，并且能够产生稀疏性，使得较弱的输入被抑制掉。因此Relu函数一般使用在隐藏层中，也是本文中使用的最多的激活函数。
Sigmoid函数： 数学表达式为$f(x)=\frac{1}{1+e^{-x}}$，Sigmoid函数将输入映射到0到1之间的连续输出。它的值在接近正无穷时趋近于1，在接近负无穷时趋近于0。Sigmoid函数在神经网络的前馈过程中经常用于二分类任务。然而，由于当x足够大或者足够小时容易发生梯度消失，当网络很深时，Sigmoid函数不再被推荐使用。

双曲正切函数： 数学表达式为$f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$，双曲正切函数可以将输入映射到[-1, 1]之间的连续输出。它的值在接近正无穷时趋近于1，在接近负无穷时趋近于-1。双曲正切函数常用于神经网络的隐藏层，特别是当数据的分布比较对称时。事实观察图像Sigmoid只是双曲正切函数向上平移一个单位形成，但与Sigmoid函数相比，双曲正切函数具有更大的梯度，能够提供更强的非线性表达能力。

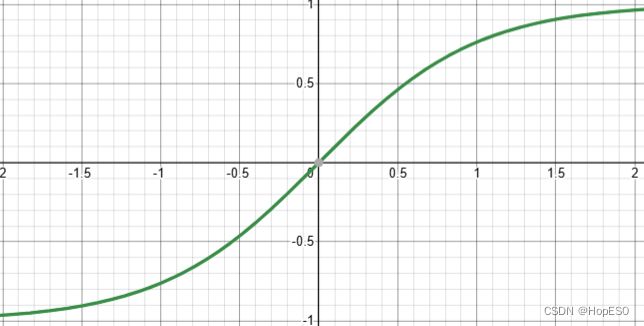
2.3.2 损失函数

之前我们学习过了交叉熵损失函数，交叉损失函数通过计算模型对每个类别的预测概率和真实类别标签之间的差异来衡量模型的性能。它评估了模型的预测结果与真实标签之间的差异，用于优化模型参数以最小化这种差异。在分类问题中我们通常会使用该函数。
对于回归问题，我们大多会采用类似于方差的形式的损失函数比如L1损失（也称作绝对值损失或平均绝对误差）和L2损失（也称作平方损失或均方误差）是常用于回归任务中的两种不同的损失函数，用来衡量预测结果与真实值之间的差异。它们具有不同的特性适用于不同的问题。
L1损失：$$L=\frac{1}{N}\sum _{i=1}^N|y_i-\widehat{y_i}|$$
L1损失是预测值与真实值之间差的绝对值的平均。它对离群点比较鲁棒，因为在计算损失时不会像平方损失那样对差值进行平方，而是保留了原始的线性差值。并且对异常值敏感，因为在差值相等的情况下，梯度始终是恒定的，没有逐渐减小的趋势。这可能导致模型更偏向于拟合异常值。

L2损失： $$L=\frac{1}{N}\sum _{i=1}^N(y_i-\widehat{y_i}{)}^2$$
L2损失是预测值与真实值之间差的平方的平均。它将差值平方，因此对大的差异更加敏感，并且与L1损失相比，平方项的特性提供了更平滑的梯度下降。所以L2损失在回归任务中是常用的一种选择，尤其是当数据中没有明显的离群点时。通过平方项，L2损失使模型更关注较大的预测误差，有助于减小整体的误差。

第三章 案例实战

如看到这里，对上述一些数学推导仍然感到困惑，并不是什么问题，这得感谢pytorch的研发者，为我们集成如此优秀的开发库。在实战过程中，我们不需要手写反向传播，也不需要手写优化算法，只需要将这些模块按照自己的需求连接起来，就像拼积木一般，当然如果能完全理解里面的数学逻辑自然最好不过，接下来我们来拼“乐高”。

3.1如何选择模型？

在解决一个实际问题之前，需要先判断问题的属性。实际问题通常分为两类回归问题和分类问题。图片引用自

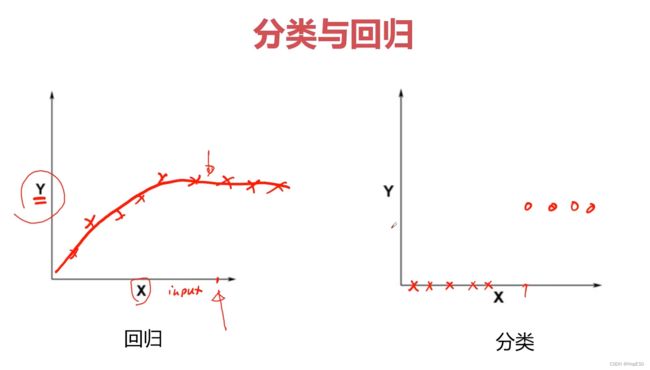
在回归问题中，我们的目标是预测一个连续数值的输出。回归任务的目标是找到输入与输出之间的关系，并建立一个函数来对新的输入进行预测。例如：房价预测、销售额预测、股票价格预测等。在这些问题中，我们需要根据输入的特征（如房屋的面积、市场营销活动的投入）来预测一个连续的输出值（如房价、销售额、股票价格）。
分类问题是将输入数据划分到不同的类别或标签中。目标是根据已知的样本数据构建一个分类模型，以便对未知样本进行分类预测。些分类问题的例子包括电子邮件垃圾分类、图像识别中的物体分类、疾病预测等。在这些问题中，我们需要根据已有样本的特征（如邮件的文本内容、图像的像素值）来预测输入属于哪个类别（如垃圾邮件/非垃圾邮件、狗/猫、健康/患病）。
但实际上，回归问题和分类问题之间没有明确的界限，因为一些任务可能具有混合特性。例如，预测房价可以被认为是一个回归问题，但如果将其转化为预测高/中/低三个价格范围，则可视为分类问题。适当选择任务类型和方法取决于数据集的特点和预测需求。

3.2如何判断模型的优劣？

判断模型的优劣通常涉及多个评估指标，根据具体任务和需求选择适合的度量指标。例如损失函数、方差、准确率、特定领域的评估指标、交叉验证等。通过这些指标我们我可以将模型的训练结果分为两个极端：欠拟合、过拟合。

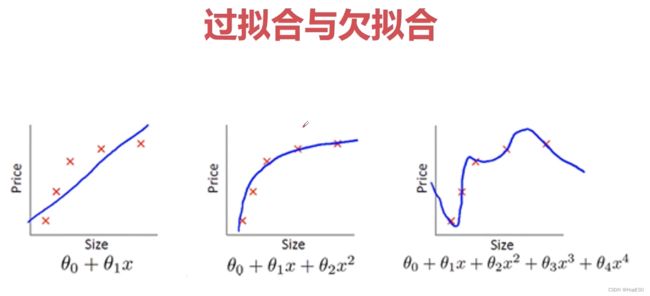
欠拟合发生时，模型在训练数据和未见过的新数据上都表现不好，误差都较高，如第一个曲线所示。通常是由于模型过于简单，无法捕获数据中的复杂关系导致的。针对这一问题，可以增加模型复杂度，使用更多的特征或增加模型的参数数量。或者考虑非线性关系，引入多项式特征或非线性函数变换。也可以使用更复杂的模型算法，如深度神经网络，增加训练迭代次数，使模型有足够的训练时间来适应数据。除此之外，也可以对数据集进行扩充，利用Gan网络或者其他手段丰富数据集。
过拟合发生时，模型在训练数据上表现良好，但在新的未见过的数据上预测性能较差。这通常是由于模型太复杂或训练数据不足导致的。当模型很复杂（例如参数过多或特征过多）且与训练数据的噪声相对应时，容易发生过拟合。对此我们也有许多方法，收集更多的训练数据，以便更好地反映整体样本分布。减小模型的复杂度，如减少模型的参数数量、使用正则化方法（如L1或L2正则化）限制参数大小。使用特征选择方法，选择对预测目标最重要的特征。采用交叉验证等模型选择技术选择适当的模型。这些防止模型过拟合的方法，也被一些学者统称为正则化。例如在VGG这种复杂度很高的模型的全连接层中就采用了随机失活的正则化方法，是随机使一些神经元不参与模型运行，防止过拟合。

3.3波士顿房价预测

数据可以在http://t.cn/RfHTAgY下载。
在这个案例中，一共有十三个数据会影响最终的房价。模型的目标是预测房价的走势，是典型的回归问题。
显然，对于导入的整体数据我们需要对矩阵进行分割，每一行代表一次输入与实际的输出，定义输入矩阵为$x^{[i]}=[x_1^{[i]},x_2^{[i]},x_3^{[i]},...,x_{13}^{[i]}]$其中i为样本的次序，角标代表不同的输入属性。定义$y$实际房间，网络结构选择100个神经元的单层神经网络，后续再进行优化。
数据处理
读取数据信息，这里我已经将数据下载到py文件同一目录下，命名为housing.data。

ff=open("housing.data").readlines()
data=[]
for item in ff:
    out=re.sub(r"\s{2,}"," ",item).strip()#将多个空格合并为一个
    data.append(out.split(" "))
#将data转换为浮点
data= np.array(data).astype(np.float32)

读取数据后可以发现一共有506条数据，将其分为496大小的训练样本与10大小的测试样本。分类时采用随机的方法选择样本。

#打乱data的顺序
np.random.shuffle(data)
#设置输入与输出
Y=data[:,-1]
X=data[:,0:-1]
Y_train=Y[0:496]
Y_test=Y[496:]
X_train=X[0:496,:]
X_test=X[496:,:]

可以将数据的维度打印出来判断数据是否被正确分割了。

print(X_test.shape)
print(Y_test.shape)
print(Y_train.shape)
print(X_train.shape)
#结果
(10, 13)
(10,)
(496,)
(496, 13)

网络结构
接下来设置网络结构，使用面向对象编程中的继承方法调用父类torch.nn.Module中的属性。随后定义网络结构的传递顺序，也就是正向传播。在经过为一的隐藏层后，使用relu函数做为激活函数，增加非线性，以提高模型的泛型。这里激活函数与网络结构都是比较简单的，且一定不是最优，我们需要通过观察模型迭代的结果来调整优化模型。

class Net(torch.nn.Module):
    def __init__(self,n_feature,n_output):
        super(Net,self).__init__()#继承父类torch.nn.Module中的属性创建网络
        self.hidden=torch.nn.Linear(n_feature,100)
        self.predict=torch.nn.Linear(100,n_output)
        # 随机初始化权重
        torch.nn.init.normal_(self.hidden.weight)
    def forward(self,x):
        out=self.hidden(x)
        out=torch.relu(out)
        out=self.predict(out)
        return out
net=Net(13,1)#输入与输出个数

同样在这个过程后，我们也可以加一些程序查看网络结构是否正确生成。

model = create_your_model()  # 这里需要指定自己的模型，比如案例中的net

# 计算参数数量
total_params = sum(p.numel() for p in model.parameters())
print(f"Total parameters: {total_params}")

# 查看各层的参数数量
for name, param in model.named_parameters():
    print(f"Layer: {name}, Parameters: {param.numel()}")

损失函数与优化方案
由于模型解决的是回归问题，预测的房价应该是一条随着13个变量变化而变换的连续数据，这里我使用了L2损失函数。优化方案选择Adm。

loss_funcation=torch.nn.MSELoss()#L2损失函数
loss_=np.zeros(10000)
I =np.arange(1,10001)
#优化器
optimiter=torch.optim.Adam(net.parameters(),lr=0.001,betas=(0.9, 0.999),eps=1e-08,weight_decay=0,amsgrad=False)

设置训练模块
这里需要注意的是，经过网络返回的pred值维度是否与真实值y_data相同。这里我还使用了loss_来储存所有的损失函数以便绘图，观察迭代效果。最后也可以print几个pred和y_data,观察在迭代过程中是否越来越接近。

for i in range(10000):#迭代10000次
    x_data=torch.tensor(X_train,dtype=torch.float32)
    y_data=torch.tensor(Y_train,dtype=torch.float32)
    pred=net.forward(x_data)#返回值是（496，1）的矩阵，而y_data是（496）矩阵
    pred=torch.squeeze(pred)
    loss=loss_funcation(pred,y_data)
    loss_[i]=loss
    optimiter.zero_grad()
    loss.backward()#反向传播
    optimiter.step()
    print("迭代次数：{}，误差损失：{}".format(i+1,loss))
    #print(pred[0:10])
    #print(y_data[0:10])
    #结果
迭代次数：10000，误差损失：22.832136154174805

设置测试模块

x_data=torch.tensor(X_test,dtype=torch.float32)
y_data=torch.tensor(Y_test,dtype=torch.float32)
pred=net.forward(x_data)#返回值是（496，1）的矩阵，而y_data是（496）矩阵
pred=torch.squeeze(pred)
loss=loss_funcation(pred,y_data)
print(pred[0:10])
print(y_data[0:10])
print("误差损失：{}".format(loss))
#结果
tensor([36.3053, 13.5195,  8.5541, 20.7677, 23.4805, 30.9864, 17.6439, 21.5917,
       26.1236, 49.3287], grad_fn=<SliceBackward0>)
tensor([32.9000,  7.0000, 13.1000, 19.2000, 20.7000, 31.6000, 19.1000, 21.0000,
       28.7000, 50.0000])
误差损失：20.732263565063477

绘图

 print(loss_)
print(I)
plt.plot(I,loss_)
plt.show() 

分析模型
那么根据测试模块与训练模块返回的数据我们可以看到，无论是测试集还是训练集都存在较大的误差，这说明模型是欠拟合的，我们需要改进模型，尝试增加模型的深度。增加了第二个隐藏层具有50个神经元。

class Net(torch.nn.Module):
   def __init__(self,n_feature,n_output):
       super(Net,self).__init__()#继承父类torch.nn.Module中的属性创建网络
       self.hidden1 = torch.nn.Linear(n_feature,100)
       self.hidden2 = torch.nn.Linear(100, 50)
       self.predict = torch.nn.Linear(50,n_output)
       # 随机初始化权重
       torch.nn.init.normal_(self.hidden1.weight)
       torch.nn.init.normal_(self.hidden2.weight)
   def forward(self,x):
       out = self.hidden1(x)
       out = torch.relu(out)
       out  = self.hidden2(out)
       out = torch.relu(out)
       out = self.predict(out)
       return out
net=Net(13,1)
#结果
训练集：误差损失：17.748455047607422
测试集：误差损失：10.546122550964355

很明显误差减少了，说明这个改进是有效果的，但仍然有误差。我们可以继续增加网络的深度或者增加其迭代次数，那么如何判断这个模型往哪一方面改进呢？
看损失与迭代次数的图像：
相较于改进前的损失图像很大区别是，之前的损失曲线依然呈下降趋势，这说明模型并没有完全收敛，需要增加迭代次数。而增加深度后的模型趋于平滑，这说明模型已经收敛，在增加迭代次数也无法减小损失。另外曲线出现的剧烈抖动，这有可能在模型即将收敛时，学习率仍然较高的原因，也有可能由于模型在训练过程中逐渐学习到训练集中的噪声或离群值，从而导致预测结果不稳定。
观察模型的权重：
在完成迭代后，我们可以观察模型的权重判断，模型神经元的个数是否设置合理。以下是一段统计模型权重过小值的程序，可以在模型训练完成以后执行。

threshold = 0.001  # 设置有效的阈值
params = net.named_parameters()
num_small_values = {}  # 统计每个层中小值的字典
for name, param in params:
  if 'weight' in name:  # 只针对权重矩阵参数进行处理
      small_values = torch.sum(torch.abs(param) < threshold)
      num_small_values[name] = small_values.item()# 打印每个层中小值的个数
for name, count in num_small_values.items():
  print(f"Number of small values in layer {name}: {count}")
 #结果
Number of small values in layer hidden1.weight: 0
Number of small values in layer hidden2.weight: 5
Number of small values in layer predict.weight: 1

根据设置的阈值返回的结果，网络中的神经元的个数还是较为合理的，但是拟合结果却具有较大误差，我们可以尝试继续增加模型深度。当然我们也可以从优化方案，数据预处理上进行考量综合提升模型的性能，有能力的朋友可以自行尝试。

3.4手写数字识别——多层感知机

数据可以在http://yann.lecun.com/exdb/mnist/下载。
在这个分类案例中，已经将28x28图片分成了60000张训练集与10000张测试集。但下载的数据储存方式比较特殊，要转化为我们需要的数据格式。此处使用了另一些博主代码进行预处理。数据读取，在这里我突发奇想如果将28x28的图像展开成784的一维数组，使用多层感知机建立模型，是否也可以做到卷积网络同样的精度？从理论上奖，如果将图片展开，将会丢失关键的空间信息，精度是不如卷积网络的。但实践是检验真理的唯一标准，这里做一次尝试。

class Net(torch.nn.Module):
    def __init__(self,n_feature,n_output):
        super(Net,self).__init__()#继承父类torch.nn.Module中的属性创建网络
        self.hidden1=torch.nn.Linear(n_feature,32)
        self.hidden2=torch.nn.Linear(32,32)
        self.predict=torch.nn.Linear(32,n_output)
        # 随机初始化权重
        torch.nn.init.normal_(self.hidden1.weight)
        torch.nn.init.normal_(self.hidden2.weight)
        torch.nn.init.normal_(self.predict.weight)
    def forward(self,x):
        out=self.hidden1(x)
        out=torch.relu(out)
        out = self.hidden2(out)
        out = torch.relu(out)
        out=self.predict(out)
        out=torch.nn.functional.softmax(out,1)
        return out
net=Net(784,10)

在多次改进调整模型结构之后，最终的网络结构为两层32个神经元隐藏层，模型最终输出10个标签的概率，利用交叉熵损失函数进行反向传播，其余不变这里不再赘述。最终的结果如图所示：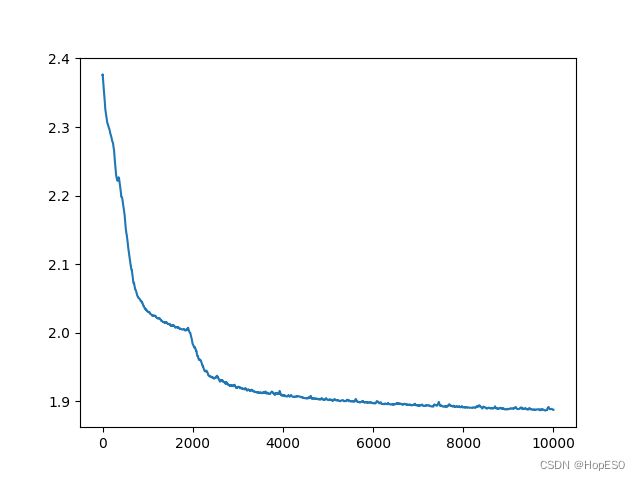
在尝试过多种模型结构之后，其中最优的误差损失：1.6964495182037354，训练准确率：76.47%。这离我们的目标相差甚远，本人水平有限，暂时也没想出来如何改进网络，使其有较好的结果，希望大家能多多交流，寻找一个更加优秀的模型。

3.5手写数字识别——卷积神经网络

如果保留图片的维度，即保存其空间信息，到底对模型性能有多大的提升呢？我们对读取图片的代码做一些修改。

import torch
import os
import struct
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
os.environ['KMP_DUPLICATE_LIB_OK'] = 'TRUE'
# 加载MNIST数据集
def load_mnist(path, kind="train"):
    # label与image数据存储路径
    labels_path = os.path.join(path, '%s-labels.idx1-ubyte' % kind)
    images_path = os.path.join(path, '%s-images.idx3-ubyte' % kind)

    with open(labels_path, 'rb') as lbpath:
        magic, n = struct.unpack('>II', lbpath.read(8))
        labels = np.fromfile(lbpath, dtype=np.uint8)

    with open(images_path, 'rb') as imgpath:
        magic, num, rows, cols = struct.unpack('>IIII', imgpath.read(16))
        images = np.fromfile(imgpath, dtype=np.uint8).reshape(len(labels), rows, cols)

    resized_images = []
    for img in images:
        img_pil = Image.fromarray(img)
        resized_img = img_pil.resize((32, 32))
        resized_img_gray = resized_img.convert('L')
        resized_images.append(np.array(resized_img_gray))

    return np.stack(resized_images), labels

# 检查是否已存在保存的数据文件
if all([os.path.exists(file) for file in ['X_train.npy', 'y_train.npy', 'X_test.npy', 'y_test.npy']]):
    X_train = np.load('X_train.npy')
    y_train = np.load('y_train.npy')
    X_test = np.load('X_test.npy')
    y_test = np.load('y_test.npy')
else:
    X_train, y_train = load_mnist("E:/VGG16/py_projects/Handwritten Digit Recognition/", kind="train")
    X_test, y_test = load_mnist("E:/VGG16/py_projects/Handwritten Digit Recognition/", kind="t10k")
    X_train = X_train.reshape(-1, 1, 32, 32)
    X_test = X_test.reshape(-1, 1, 32, 32)
    np.save('X_train.npy', X_train)
    np.save('y_train.npy', y_train)
    np.save('X_test.npy', X_test)
    np.save('y_test.npy', y_test)

在这段代码中，在原始读取图像基础之上，增加了对图片信息的完整保留最终生成的样本集维度为[60000,1,32,32],[10000,1,32,32]分别是样本数量，通道数，图片的大小。图片经过放缩至32x32，以便后续计算，通道数为1说明图像为灰度图。并且做了存储，因为每次运行代码都需要重新读取70000张图片是一个十分耗时的过程。网络结构选择LetNet_5模型，该模型是深度学习领域中的一种经典卷积神经网络模型，由 Yann LeCun 在1998年提出。它是第一个成功应用于手写字符识别任务的卷积神经网络，在手写数字识别上具有非常好的性能。

class LENET_5(torch.nn.Module):
    def __init__(self):
        super(LENET_5, self).__init__()
        self.cov1 = torch.nn.Conv2d(1, 6, (5, 5), 1, 0)
        self.cov2 = torch.nn.Conv2d(6, 16, (5, 5), 1, 0)
        self.cov3 = torch.nn.Conv2d(16, 120, (5, 5), 1, 0)
        self.liner1 = torch.nn.Linear(120, 84)
        self.liner2 = torch.nn.Linear(84, 10)

    def forward(self, x):
        x = torch.nn.functional.relu(self.cov1(x))
        x = torch.nn.functional.max_pool2d(x, (2, 2), 2)
        x = torch.nn.functional.relu(self.cov2(x))
        x = torch.nn.functional.max_pool2d(x, (2, 2), 2)
        x = torch.nn.functional.relu(self.cov3(x))
        x = x.view(x.size(0), -1)
        x = torch.nn.functional.relu(self.liner1(x))
        x = self.liner2(x)
        return x
    
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model1 = LENET_5().to(device)

该模型主要分为两个部分：卷积层和全连接层。
卷积层：
C1 卷积层：卷积核大小为（5，5），卷积核个数为6个，卷积步长为1
S2 池化层：对 C1 输出的特征图进行2x2下采样操作，取窗口中的最大值作为池化结果。通过减小分辨率来降低数据维度。
全连接层：
C3 卷积层：将 S2 的特征图与多个卷积核进行卷积，产生更高级的特征。这一步骤相当于传统神经网络中的隐含层。卷积核大小为（5，5），卷积核个数为16个，卷积步长为1。
S4 池化层：类似于 S2 层，对 C3 输出的特征图进行下采样操作。
C5 卷积层：将 S4 的特征图与多个卷积核进行卷积。同样是5x5的卷积核，个数为120个。输出[样本数，120，1，1]维度的数据进入全连接层
F6 全连接层：对 C5 层的输出进行全连接操作，得到最终的特征向量。
输出层：采用 softmax 激活函数将 F6 层的输出转化为概率值。

在执行该代码时，可能会出现GUP内存算力不够的问题，就需要采用小批量梯度下降法进行运算。

#损失函数与优化器
loss_function = torch.nn.CrossEntropyLoss()
loss_1 = np.zeros(100)
accuracy_list = []  # 用于存储每次迭代后的准确率
training_accuracy_list = []  # 用于存储训练过程中每次迭代后的准确率
optimizer = torch.optim.Adam(model1.parameters(), lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)
batch_size = 16#小批量样本个数
# 训练集
train_dataset = torch.utils.data.TensorDataset(torch.FloatTensor(X_train), torch.LongTensor(y_train))
train_data_loader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)

# 测试集
test_dataset = torch.utils.data.TensorDataset(torch.FloatTensor(X_test), torch.LongTensor(y_test))
test_data_loader = torch.utils.data.DataLoader(test_dataset, batch_size=batch_size, shuffle=False)

plt.ion()  # 开启交互模式

for i in range(100):
    loss_2 = np.zeros(len(train_data_loader))
    model1.train()  # 设置模型为训练模式
    for j, (images, labels) in enumerate(train_data_loader):
        images = images.to(device)
        labels = labels.to(device)
        optimizer.zero_grad()
        pred = model1(images)
        loss = loss_function(pred, labels)
        loss.backward()
        optimizer.step()
        loss_2[j] = loss.item()

    loss_1[i] = np.mean(loss_2)
    print("训练集【迭代次数：{}，误差损失：{}】".format(i + 1, loss_1[i]))

    # 校验准确率
    model1.eval()
    correct = 0
    total = len(test_data_loader.dataset)

    with torch.no_grad():
        for images, labels in test_data_loader:
            images = images.to(device)
            labels = labels.to(device)
            preds = model1(images)
            _, preds_class = torch.max(preds, dim=1)
            correct += (preds_class == labels).sum().item()

    accuracy = correct / total
    accuracy_list.append(accuracy)
    training_accuracy_list.append((loss_2 == 0).sum() / len(loss_2))  # 计算每次迭代后的训练集准确率
    print("训练集预测准确率：{:.2f}%".format(accuracy * 100))
    print("测试集预测准确率：{:.2f}%".format(training_accuracy_list * 100))

    # 绘制并更新可视化图表
    plt.clf()  # 清除当前图形
    plt.plot(range(1, i + 2), accuracy_list, label='Testing Accuracy')
    plt.plot(range(1, i + 2), training_accuracy_list, label='Training Accuracy')
    plt.xlabel("Iterations")
    plt.ylabel("Accuracy")
    plt.title("Training and Testing Accuracy")
    plt.legend()
    plt.draw()
    plt.pause(0.1)  # 暂停一定时间以刷新图表

    torch.save(model1.state_dict(), "LENET_5.pth")
    print("保存模型完成")

plt.ioff()  # 关闭交互模式
plt.show()  # 显示最终的图表

我在这里画蛇添足增加一个模型准确率的动态可视化。出乎意料是，模型迭代的结果非常好，并且收敛的速度非常快。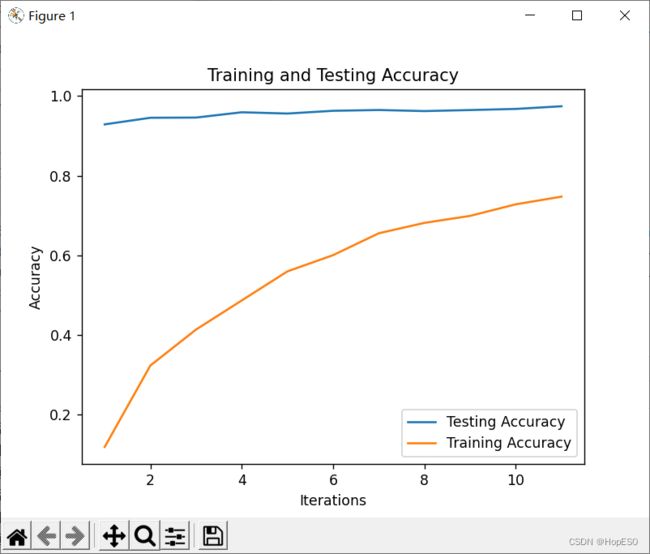
这里只迭代了几次，因为本人电脑比较差，想迭代完全耗时太久，就不进行尝试了。但从仅有几次结果来看，模型收敛速度远远快于没有卷积层的模型。这又就说，相较于数据，图片所具有空间信息十分有价值的信息，并且卷积这个数学操作可以很好提取图片的空间信息。因此研究CV方向离不开卷积神经网络。

3.6猫狗分类

猫狗分类问题相较于手写数字识别有非常多的挑战和难点。首先，猫狗图像的复杂性比手写数字要高得多，可能包含多个对象、背景干扰和噪声等因素，使得特征提取更加困难。其次，猫狗图像可能在不同的视角和尺度下进行拍摄，需要处理视角和尺度变化方面的挑战，保证模型具备一定的鲁棒性。此外，猫狗的皮毛颜色和纹理差异大，模型需要学习区分各种颜色和纹理的特征。另外，对于人来说猫和狗的区别很大，但仔细思考它们的生理结构却发现有很多的相似之处，人类区分它们业主要通过体型、耳朵形状、尾巴长度等部分位置的特征来区别，并且猫和狗之下也有不同的品种，这增加了类内变化和分类的复杂度。最后，猫狗数据集中可能存在数据不平衡问题，即猫和狗图像数量的不平衡。结合上述难点，需要采取大模型来解决这个问题，这里我们参考其他优秀的博主使用了VGG16做为模型进行预处理。
数据预处理
在案例所给的数据中一共有10000张猫的图片和10000张狗的图片，但考虑到模型需要拟合一百多万个参数，除了一些常规的处理过程之外，这里加入一些预处理方法扩充数据集。例如翻转，色域扭曲等。

import cv2
import numpy as np
import torch.utils.data as data
from PIL import  Image
def preprocess_input(x):
    x/=127.5
    x-=1.
    return x
def cvtColor(image):
    if len(np.shape(image))==3 and np.shape(image)[-2]==3:
        return image
    else:
        image=image.convert('RGB')
        return image
class DataGenerator(data.Dataset):
    def __init__(self,annotation_lines,inpt_shape,random=True):
        self.annotation_lines=annotation_lines
        self.input_shape=inpt_shape
        self.random=random

    def __len__(self):
        return len(self.annotation_lines)
    def __getitem__(self, index):
        annotation_path=self.annotation_lines[index].split(';')[1].split()[0]
        image=Image.open(annotation_path)
        image=self.get_random_data(image,self.input_shape,random=self.random)
        image=np.transpose(preprocess_input(np.array(image).astype(np.float32)),[2,0,1])
        y=int(self.annotation_lines[index].split(';')[0])
        return image,y
    def rand(self,a=0,b=1):
        return np.random.rand()*(b-a)+a

    def get_random_data(self,image,inpt_shape,jitter=.3,hue=.1,sat=1.5,val=1.5,random=True):

        image=cvtColor(image)
        iw,ih=image.size
        h,w=inpt_shape
        if not random:
            scale=min(w/iw,h/ih)
            nw=int(iw*scale)
            nh=int(ih*scale)
            dx=(w-nw)//2
            dy=(h-nh)//2

            image=image.resize((nw,nh),Image.BICUBIC)
            new_image=Image.new('RGB',(w,h),(128,128,128))

            new_image.paste(image,(dx,dy))
            image_data=np.array(new_image,np.float32)
            return image_data
        new_ar=w/h*self.rand(1-jitter,1+jitter)/self.rand(1-jitter,1+jitter)
        scale=self.rand(.75,1.25)
        if new_ar<1:
            nh=int(scale*h)
            nw=int(nh*new_ar)
        else:
            nw=int(scale*w)
            nh=int(nw/new_ar)
        image=image.resize((nw,nh),Image.BICUBIC)
        #将图像多余的部分加上灰条
        dx=int(self.rand(0,w-nw))
        dy=int(self.rand(0,h-nh))
        new_image=Image.new('RGB',(w,h),(128,128,128))
        new_image.paste(image,(dx,dy))
        image=new_image
        #翻转图像
        flip=self.rand()<.5
        if flip: image=image.transpose(Image.FLIP_LEFT_RIGHT)
        rotate=self.rand()<.5
        if rotate:
            angle=np.random.randint(-15,15)
            a,b=w/2,h/2
            M=cv2.getRotationMatrix2D((a,b),angle,1)
            image=cv2.warpAffine(np.array(image),M,(w,h),borderValue=[128,128,128])
        #色域扭曲
        hue=self.rand(-hue,hue)
        sat=self.rand(1,sat) if self.rand()<.5 else 1/self.rand(1,sat)
        val=self.rand(1,val) if self.rand()<.5 else 1/self.rand(1,val)
        x=cv2.cvtColor(np.array(image,np.float32)/255,cv2.COLOR_RGB2HSV)#颜色空间转换
        x[...,1]*=sat
        x[...,2]*=val
        x[x[:,:,0]>360,0]=360
        x[:,:,1:][x[:,:,1:]>1]=1
        x[x<0]=0
        image_data=cv2.cvtColor(x,cv2.COLOR_HSV2RGB)*255
        return image_data

另外吸取上一次的经验，如果我们每一次执行代码都重新读取一次图片非常耗时，并且如此大的输入矩阵，在后续打乱数据顺序等操作中也会有较大影响。于是对数据进行一个差分工作，使用一个txt文件，分别存储图片的标签，以及路径。在接下来操作中，只要打乱tex文件的顺序，逐条调用图片进行训练可以节省一些时间。

import os
classes=['cat', 'dog']
sets=['train']
if __name__== '__main__':
  wd= os.getcwd()#读取当前路径"E:\PyCharm Community Edition 2023.2\py_projects\readimage.py"
  for se in sets:#遍历sets列表中每一个元素,这里只有一个'train'
    list_file=open('cls_'+se+'.txt','w')
    datasets_path=se
    types_name=os.listdir(datasets_path)#os.listdir()方法用于返回指定名称的文件包含文件或文件夹名字的列表,这里返回的就是cat和dog
    for type_name in types_name:
     if type_name not in classes:#判断train文件的子文件名称是否在类别中
       continue
     cls_id=classes.index(type_name)#将图片的类别赋值给cls_id，猫是0，狗是1
     photos_path=os.path.join(datasets_path,type_name)#合并路径train\cat和train\dog
     photos_name=os.listdir(photos_path)#获取train\cat和train\dog下所有的文件名
     for photo_name in photos_name :
       _,postfix=os.path.splitext(photo_name)#该函数用于分离文件名与拓展名
       if postfix not in['.jpg','.png','.jpeg']:
          continue
       list_file.write(str(cls_id)+';'+'%s/%s ' %(wd,os.path.join(photos_path,photo_name)))#组合路径与文件名写入cls——train.txt
       list_file.write('\n')
list_file.close()

网络结构的搭建
这里直接采用了pytorch官方给的VGG16的代码，并且我们使用VGG16预训练好的参数进行训练，可以在较少的迭代次数中收敛。

import torch
import torch.nn as nn
from torch.hub import load_state_dict_from_url


model_urls = {
    "vgg16": "https://download.pytorch.org/models/vgg16-397923af.pth",
}#权重下载网址，会导入训练好的权重与偏置项


class VGG(nn.Module):
    def __init__(self, features, num_classes = 1000, init_weights= True, dropout = 0.5):
        super(VGG,self).__init__()
        self.features = features#features 参数就是这个包含卷积层和池化层的列表，由makelayers（）生成
        #生成全连接层
        self.avgpool = nn.AdaptiveAvgPool2d((7, 7))#AdaptiveAvgPool2d使处于不同大小的图片也能进行分类
        self.classifier = nn.Sequential(
            nn.Linear(512 * 7 * 7, 4096),
            nn.ReLU(True),
            nn.Dropout(p=dropout),
            nn.Linear(4096, 4096),
            nn.ReLU(True),
            nn.Dropout(p=dropout),#完成4096的全连接
            nn.Linear(4096, num_classes),#对num_classes的分类
        )
        if init_weights:#intit_wights=ture,初始化权重
            for m in self.modules():#m为每个层的权重，维度与大小已经被定义。
                if isinstance(m, nn.Conv2d):#判断m是否属于卷积层
                    nn.init.kaiming_normal_(m.weight, mode="fan_out", nonlinearity="relu")#使用Kaiming正态分布初始化方法(nn.init.kaiming_normal_)初始化权重，并使用常数值初始化偏置项。
                    if m.bias is not None:
                        nn.init.constant_(m.bias, 0)
                elif isinstance(m, nn.BatchNorm2d):
                    nn.init.constant_(m.weight, 1)
                    nn.init.constant_(m.bias, 0)
                elif isinstance(m, nn.Linear):
                    nn.init.normal_(m.weight, 0, 0.01)#使用正态分布初始化方法(nn.init.normal_)初始化权重，并使用常数值初始化偏置项。
                    nn.init.constant_(m.bias, 0)
    #该函数将最后一个池化层的输出7*7*512的矩阵转换为一维向量
    def forward(self, x):
        x = self.features(x)
        x = self.avgpool(x)
        x = torch.flatten(x, 1)#对输入层进行平铺，转化为一维数据
        x = self.classifier(x)
        return x

#网络结构生成器，生成对应的卷积网络结构，如vgg16结构层次为
#最大池化层，使用2x2的窗口和2步长
#两个3x3的卷积层，输出通道数为128
#最大池化层，使用2x2的窗口和2步长
#三个3x3的卷积层，输出通道数为256
#最大池化层，使用2x2的窗口和2步长
#三个3x3的卷积层，输出通道数为512
#最大池化层，使用2x2的窗口和2步长
#三个3x3的卷积层，输出通道数为512
#最大池化层，使用2x2的窗口和2步长
def make_layers(cfg, batch_norm = False):#make_layers对输入的cfg进行循环
    layers = []
    in_channels = 3
    for v in cfg:#对cfg进行输入循环,取第一个v
        if v == "M":#如果V的大小等于“M”，则为池化层
            layers += [nn.MaxPool2d(kernel_size=2, stride=2)]#把输入图像进行缩小
        else:
            conv2d = nn.Conv2d(in_channels, v, kernel_size=3, padding=1)#输入通道是3，输出通道64
            if batch_norm:
                layers += [conv2d, nn.BatchNorm2d(v), nn.ReLU(inplace=True)]
            else:
                layers += [conv2d, nn.ReLU(inplace=True)]#inplace=ture表示使用向量计算
            in_channels = v#迭代通道数
    return nn.Sequential(*layers)#nn.Sequential(*layers) 表达式中的 * 符号用于展开 layers 列表，将其中的每个层作为参数传递给 nn.Sequential()。这样，nn.Sequential 就会将所有的层按顺序加入到一个顺序容器对象中，并将该容器作为函数的返回值。


cfgs = {
    "D": [64, 64, "M", 128, 128, "M", 256, 256, 256, "M", 512, 512, 512, "M", 512, 512, 512, "M"],

}

def vgg16(pretrained=False, progress=True,num_classes=2):
#pretrained=False 表示是否加载预训练的权重。预训练的权重可以通过设置 pretrained=True 来自动下载和加载。
#progress=True 表示在下载和加载权重时，是否显示进度条。
#num_classes=2 表示输出层的类别数量，默认为2（二分类问题）
    model = VGG(make_layers(cfgs['D']))#make_layers(cfgs['D'])为生成的卷积层,VGG()补全全连接层。
    if pretrained:
        state_dict = load_state_dict_from_url(model_urls['vgg16'],model_dir='./model' ,progress=progress)#预训练模型地址
        model.load_state_dict(state_dict)
    if num_classes !=1000:#vgg全连接层最终输出为1000个特征，如果判断类别不等于1000，则替换全连接层
        model.classifier = nn.Sequential(
            nn.Linear(512 * 7 * 7, 4096),
            nn.ReLU(True),
            nn.Dropout(p=0.5),#随机删除一部分不合格
            nn.Linear(4096, 4096),
            nn.ReLU(True),#防止过拟合
            nn.Dropout(p=0.5),
            nn.Linear(4096, num_classes),
        )
    return model

最后也希望大家也可以尝试一下使用卷积层代替全连接层的结构，看是不是可以优化迭代速度。我为什么不试一下？因为我的电脑算冒烟了都没迭代出一次。所以拜托大家了。我在这里也放上源码与数据的链接，还望各位不吝赐教我这个小白。
链接：https://pan.baidu.com/s/1ZekaHpzm2yfH7vhrR3coTg?pwd=hj33
提取码：hj33

import torch
class VGG16(torch.nn.Module):
    def __init__(self, Xshape, Yshape):
        super(VGG16, self).__init__()
        self.blook1 = torch.nn.Sequential(torch.nn.Conv2d(3, 64, (3, 3), 1, 1)
                                          , torch.nn.ReLU()
                                          , torch.nn.Conv2d(64, 64, (3, 3), 1, 1)
                                          , torch.nn.ReLU()
                                          , torch.nn.MaxPool2d((2, 2), 2))
        self.blook2 = torch.nn.Sequential(torch.nn.Conv2d(64, 128, (3, 3), 1, 1)
                                          , torch.nn.ReLU()
                                          , torch.nn.Conv2d(128, 128, (3, 3), 1, 1)
                                          , torch.nn.ReLU()
                                          , torch.nn.Conv2d(128, 128, (3, 3), 1, 1)
                                          , torch.nn.ReLU()
                                          , torch.nn.MaxPool2d((2, 2), 2))
        self.blook3 = torch.nn.Sequential(torch.nn.Conv2d(128, 256, (3, 3), 1, 1)
                                          , torch.nn.ReLU()
                                          , torch.nn.Conv2d(256, 256, (3, 3), 1, 1)
                                          , torch.nn.ReLU()
                                          , torch.nn.Conv2d(256, 256, (3, 3), 1, 1)
                                          , torch.nn.ReLU()
                                          , torch.nn.MaxPool2d((2, 2), 2))
        self.blook4 = torch.nn.Sequential(torch.nn.Conv2d(256, 512, (3, 3), 1, 1)
                                          , torch.nn.ReLU()
                                          , torch.nn.Conv2d(512, 512, (3, 3), 1, 1)
                                          , torch.nn.ReLU()
                                          , torch.nn.Conv2d(512, 512, (3, 3), 1, 1)
                                          , torch.nn.ReLU()
                                          , torch.nn.MaxPool2d((2, 2), 2))
        self.blook5 = torch.nn.Sequential(torch.nn.Conv2d(512, 512, (3, 3), 1, 1)
                                          , torch.nn.ReLU()
                                          , torch.nn.Conv2d(512, 512, (3, 3), 1, 1)
                                          , torch.nn.ReLU()
                                          , torch.nn.Conv2d(512, 512, (3, 3), 1, 1)
                                          , torch.nn.ReLU()
                                          , torch.nn.MaxPool2d((2, 2), 2))
        self.inchannels = int(Xshape * Yshape * 512 / 1024)
        self.blook6 = torch.nn.Sequential(torch.nn.Conv2d(self.inchannels, 4096, (1, 1), 1, 0)
                                          , torch.nn.ReLU()
                                          , torch.nn.Conv2d(4096, 4096, (1, 1), 1, 0)
                                          , torch.nn.ReLU()
                                          , torch.nn.Conv2d(4096, 1000, (1, 1), 1, 0)
                                          , torch.nn.ReLU()
                                          , torch.nn.Conv2d(1000, 1, (1, 1), 1, 0))