基于matlab的图像去噪算法设计与实现
摘 要
随着我们生活水平的提高,科技产品飞速更新换代,在信息传输中,图像传输所占的比重越来越大。但自然噪声会在图像传输时干扰其传输过程,甚至会使图片不能表达其原来的意义。去噪处理就是为了去除图像中的噪声,从而提升图像质量。因此,研究针对噪声的去噪方法是十分必要的。
文中首先分析了几种图像的去噪算法相关知识。有许多类型的图像去噪法,可以分为以下两种方法:空间滤波和频率场滤波。 本文主要介绍了中值滤波、均值滤波、频域低通滤波去噪算法。 首先,嵌入它们的共同功能及其在图像处理应用中的用途。 其次,阐述了一些去噪算法的原理和特点。 最后,matlab用于对图片模拟和去噪。
Matlab仿真结果表明,不同的去噪算法各有优势。在这些去噪算法中,均值滤波是一种较为普遍的线性滤波,一般适用于高斯噪声的类型。中值滤波是一种比较常见的非线性过滤,特别是对于椒盐噪声,使用中值滤波法效果更佳。因此,在对一幅图片进行去噪操作之前,首先要分析噪声的类型以及其产生的原因,然后再选择合适的去噪算法,这样才能达到比较好的去噪效果。
关键词:图像噪声;图像去噪算法;中值滤波;均值滤波;matlab。
Abstract
With the improvement of our living standards and the rapid upgrading of technology products, image transmission accounts for a larger proportion in information transmission. However, natural noise will interfere with the transmission process during image transmission, and even the picture cannot express its original meaning. Denoising is done to remove noise from the image and improve image quality. Therefore, it is necessary to study the denoising method for noise.
In this paper, the knowledge of several images of denoising algorithms is first analyzed. There are many types of image denoising methods that can be divided into the following two methods: spatial filtering and frequency field filtering. This paper mainly introduces median filtering, mean filtering, and frequency domain low-pass filtering denoising algorithms. First, embed their common features and their use in image processing applications. Secondly, the principles and characteristics of some denoising algorithms are expounded. Finally, matlab is used to simulate and denoise pictures.
Matlab simulation results show that different denoising algorithms have their own advantages. Among these denoising algorithms, mean filter is a more general linear filter, which is generally applicable to the type of Gaussian noise. Median filtering is a common non-linear filtering, especially for salt and pepper noise, the use of median filtering method is better.Therefore, before denoising a picture, first analyze the type of noise and the cause of the noise, and then select the appropriate denoising algorithm, in order to achieve a better denoising effect.
Key words: Pattern Noise ; Image Denoising Algorithm ; Median Filtering ; Mean filtering ; Matlab.
目 录
摘 要 III
Abstract III
第1章 绪论 4
1.1 课题研究背景 4
1.2 国内外研究现状 4
1.3 课题研究重点和思路 5
第2章 Matlab图像处理基础 6
2.1 Matlab概述 6
2.2 Matlab的主要功能 6
2.2.1 数值计算和符号计算功能 6
2.2.2 绘图功能 6
2.2.3 语言体系 7
2.2.4 Matlab工具箱 7
第3章 图像与噪声 9
3.1 什么是图像噪声 9
3.2 图像噪声的分类 9
3.2.1 按噪声产生的原因分类 9
3.2.2 按噪声和信号的关系分类 9
3.2.3 按噪声幅度分布的统计特征分类 10
3.3 图像噪声的特点 11
第4章 空域去噪算法及仿真 12
4.1 均值滤波法 12
4.1.1 均值滤波的基本原理 12
4.1.2 均值滤波的缺点 12
4.2 中值滤波 14
第5章 频域低通滤波 16
5.1 几种常用的低通滤波器 16
5.1.1 理想低通滤波器(ILPF) 16
5.1.2 Butterworth低通滤波器(BLPF) 17
5.1.3 指数低通滤波器(ELPF) 18
5.1.4 梯形低通滤波器(TLPF) 18
5.2 频域低通滤波在Matlab中进行仿真 20
第6章 图像去噪质量评价 24
6.1 主观判断 24
6.2 客观判断 24
6.2.1 均方信噪比(SNR) 24
6.2.1 Matlab中计算 25
第7章 总 结 28
7.1 总 结 28
7.2 展 望 28
参考文献 29
致 谢 31
第1章 绪 论
1.1 课题研究背景
在如今的这个信息时代,图像传输的作用越来越明显。相比于文字载体而言,图像更为直接、明了,且所赋予的内容也更加丰富。可见图像在人类传递信息的整个过程中也发挥了重要的作用。然而在图像的获取和传输过程中,很容易出现图像噪声的情况,图像噪声的存在对人们的视觉感官有着很大的影响,甚至会影响到对图像的获得和理解。因此,对图像进行去噪处理使图像在传输过程中非常重要的一个步骤,图像只有清晰,人眼和计算机才能够采取到其所包含的重要信息。
对图像进行去噪可以分为两类:空间去噪和变换去噪。 就如大家所知道的,在信息传输中,图像载体比较受到欢迎。而图像由各种像素组成,在进行去噪的时候,采用空间去噪法,可以直接处理图像像素。 除了这些之外,常用的方法还包括中值滤波、均值滤波等。变换域去噪法不是直接在图像本身进行去噪,而是图像被变换,然后处理系数以进行处理。 在处理然后对由表格处理的图像进行逆变换之后,公共域变换域去噪基于基于小波变换的傅里叶变换。图像去噪和图像去噪是两个主要类别。
在科研、军事技术、工农业生产、医疗、气象条件这几种领域里都广泛运用到图像处理技术。然而,在很多情况下,图像噪声会影响图像的传输,图像的有效信息也得不到良好的体现。因此,对图像去噪算法进行深入研究,有重要的现实意义。
1.2 国内外研究现状
图像去噪方法可以从不同处理领域的角度划分空间和频率处理方法。然而,空间滤波理论更加成熟,数字分析简单,无信号的噪音不一致无疑是有效的。但是,在图像边缘保护方面,空间域是相对较差的。非线性滤波在运用过程中,主要充分考虑到人们的视觉标准不一,加上最佳滤波的原理的限制,所以非线性滤波可以提高图像分辨率和边缘的保护。
对于传统的空间滤波方法而言,存在着一定的局限性,比如传统的空间滤波方法不能有效地区分信号的高频部分和高频噪声部分。因此,图像信息很容易丢失在过滤高频噪声的过程中,并且,还会导致整个图像失真,影响图像所要表达的重要信息。频域滤波与传统的空间滤波方法相比,就比较具有优势。所谓频域滤波,就是通过频域滤波分析和处理频域中的图像系数。在进行频域滤波去噪之前,要求我们首先将图像转换为频域的图像。在处理频域系数之后,执行逆变换以形成精细图像。傅里叶经典变换将图像转换为空间和频率域,并且,使用此种方法,还可以综合考虑其他问题。因此,频域滤波在传统的数字图像处理中,扮演着重要角色。例如,采样点,数字化系统,卷积滤波器等。并具有优异的特性,如线性度,时移,对称性,频移等。然而,傅立叶变换也是具有局限性的,其不适用于非平稳信号分析,并且只能随时间提供频率特性。为了改善这种差距,才提出了小波理论。
Weaver首先使用小波阈值去噪方法。 在进行去噪的过程中,并不是直接进行的,Weaver会转换图像,将其转换为波场,然后再对转换过的小波系数进行处理,该波长系数是与阈值相比的波长系数。保持或修改比率很大,否则设置为零。然后,Donoho对去噪小波算法进行了深入细致的分析,并对其特征进行了解释,为接下来研究小波去噪和小波去噪的发展奠定了一定的基础。
Nason与Weaver不一样,他提出了另一种阈值方法,其阈值选择基于交叉验证标准。通常,难以准确地计算噪声方差。由于噪声的产生,具有一定的偶然性,因此,Nason的方法不需要计算噪声方差。使用该方法进行去噪,因此增益阈值更准确,但使用该方法所需的计算量很大,并且还同时属于波变换和逆变换。
Kivanc,John和Xu等人提出的去噪小波方法,是现如今最为常用的方法,其分别是利用投影方法和类似方法来实现。顾名思义,基于贝叶斯评估理论的去噪方法,在进行去噪的过程中,提供了小波系数的最佳估计,最小化了贝叶斯估计的风险。使用此方法进行去噪,所取得的效果会优于其他方法。
小波理论具有精确的时域定位能力和频域定位能力,能够解决许多傅里叶变换无法解决的难题。近年来,许多学者对小波领域进行了大量的研究,取得了一系列的成果,使小波理论发展成为一个完整的理论体系,并在图像去噪中得到了广泛的应用。
1.3 课题研究重点和思路
本文主要对空间域和领率域的滤波算法进行了研究,主要写作构思如下:
第1章为绪论部分,这一部分主要介绍了本次课题的研究背景、研究对象、研究意义,以及国内外研究现状。
第2章简要概述了matlab这一软件的来源与使用,本次研究中主要是运用matlab进行仿真与实现。
第3章概述了图像噪声的性质,包括了噪声的含义、分类以及产生的原因,介绍了生活中比较常见的噪声。
第4章介绍了空域去噪算法并进行仿真,主要是对均值滤波和中值滤波这两大方法进行研究与仿真。
第5章则讲述了频域低通滤波,包括几种常见的滤波器,并且对其传递函数和三维透视图进行分析和研究,对理想低通滤波进行了仿真。
第6章是本文整体的一个总结,同时对整个论文中的不足以及对未来工作进行分析和展望。
第2章 Matlab图像处理基础
2.1 Matlab概述
Matlab(Matrix Laboratory)是由美国Mathworks公司所研究开发的一款软件,它被人们广泛应用于科学计算领域,数值分析领域,工程计算领域,自动控制领域等科学工程领域。它除了具备复杂的矩阵和计算器功能外,还能将其运用到许多专业领域的仿真处理和设计任务完成,同时还能利用Matlab的自动生成特性,将其直接连接到硬件代码。Matla不仅功能强大,而且易学易用。Matlab集成了矩阵运算,数值分析,图形处理和编程技术等多种功能于一体,是一个强大的分析和编程工具,深受用户喜爱。除了能够进行数据分析和编程之外,Matlab还可用于故障排除,特别是对于科学与工程问题而言,Matlab所发挥的重要是不容小觑的。它还提供符号专业级计算,文字处理,可视化建模仿真和实时控制。Matlab是具有语言功能的新一代软件开发平台。
经过多年的发展与进步,现如今,Matlab已能做到适用于多学科领域、多任务处理和强大平台对接,是一款逐渐趋于成熟的大型软件。在当前环境下,Matlab还已经发展成为了当代大学生需要掌握的基本技能,说明Matlab开始具有普适性且被广泛接受。同时Matlab还被广泛应用在一些较为严谨的设计研究单位以及相关工业发展部门,其主要目的是用于研究技术创新和解决相关具体问题,这在一定程度上节省了不少人力成本和时间成本。在中国,Matlab的使用范围也是比较普遍,也逐渐开始受到了重视,Matlab在很短一段时间内收获了无数用户,并且深受喜爱,好评颇高,因为任何学科或工程领域,在使用Matlab时,都可以找到合适的功能来解决他们的问题。
2.2 matlab的主要功能
自从MathWorks公司于1984年将Matlab引入市场以来,在全世界范围内产生了巨大的影响。至今为止,Matlab已经被使用了20余年,并且在不断发展,市场竞争也十分激烈。Matlab不仅具有可靠的数值计算和符号计算,强大的绘图功能,关键是其的语言系统还易于学习,加上拥有大量应用工具,使得matlab与其他技术应用相比较而言,具有相当明显的使用优势与功能价值。
2.2.1数值计算和符号计算功能
MATLAB将数学中的矩阵形式作为相关数据操作的基本要素,从而促使矩阵运算更加简便与高效。在MATLAB所具有的功能中,其数值计算方法被称为世界上最先进,最可靠的方法。 并且MATLAB的程序得到了世界级专家的高度优化。 如此一来,更进一步的提升了MATLAB的影响力。
在实际应用中,除了数值计算之外,通常还需要针对与符号信息技术领域相关的问题的分析解决方案。 MATLAB结合了Maple语言之后就成为了计算符号特征。
2.2.2绘图功能
MATLAB在可视化方面,较为强大,其可提供各种图形,包括2D图形和3D图形,以及修改和控制图形,以此来达到提高图形性能的目前。除此之外,MATLAB还可以轻松添加图形,标题,轴等。 可以为3D图形添加视觉,颜色控制和灯光效果。 此外,Matlab软件还可以创建3D动画效果,以及隐式函数图等,可用于科学计算和工程图纸。 对此,使用MATLAB进行图形处理操作有很多优势,用户可以在进行图形操作处理时,更加的方便灵活,并且性能空间不受限制。
2.2.3语言体系
MATLAB具有针对程序内部结构,调用函数使用,数据整体结构,输入和输出状态以及面向对象编程语言等对象的控制协调作用。因此,MATLAB的使用也可以用作传统的编程语言,如BASC,FORTRAN和C.MATLAB,易于学习,易于编程。因此,对于从事数值计算工作,计算机设计工作和系统仿真工作的人来说,优先考虑到的就是运用MATLAB编程。
MATLAB是一种解读释义性语言,在运行起来时,速度较慢,并且,在MATLAB环境中是无法进行独立运行的,需求其他程序的辅助。 Math Works在创立MATLAB时,目的是使MATLAB成为现今社会普遍适应的软件开发工具。Math Works提供了一个用于可在EXE文件上进行MATLAB源程序编译的编译器。这些文件独立于集成的MATLAB环境,并在编程程序中转换为MATLAB C.
2.2.4MATLAB工具箱
MATLAB由两部分组成:不同的基础知识和各种可选工具。 基础知识是MATLAB的核心内容,也是工具箱的构建基础。 MATLAB工具箱有两种类型:Function Toolbox和Disciplinary Toolbox。 Functional Toolbox的主要功能是:对符号计算器进行功能扩展,进行可视化建模和模拟可视化、文本处理等功能。Disciplinary Toolbox是高度专业化的,例如系统控制系统,安全开发系统,正常网络规则,优化系统和金融资产。这些工具由该领域的高学术学者编写,他们可以将这些工具直接用于类似领域的科学研究。
第3章 图像与噪声
图像噪声对图像的传输有很大的影响,一张图片在正常的传输下可以比较完好地传递出图像的信息。但由于图像受噪声干扰,图中的信息无法正常传递。传递中的噪声容易形成,所以去噪显得尤为重要。
3.1图像噪声的定义
图像噪声是指图像在传输中出现的干扰传输过程的因素以及传输完成后产生的不必要多余信息。图像噪声可以被理解为在接收或发送图像时接收的干扰的奇数信号,并且通常由概率分布函数和概率密度分布函数来描述。有的噪声会使图像变得模糊不清,有的则直接阻碍信息的传递。有的噪声相对独立,噪声也可能相互关联。为了有效地降低噪声,必须根据不同的情况来选择合理适应的方法。
3.2 图像噪声的类型
3.2.1 按噪声产生的原因进行划分
图像噪声产生的原因是复杂多样的,依据噪声产生的原因进行分类划分,一般可将其分为内部噪声和外部噪声两种类型。外部噪声即外在原因感染产生的图像噪声,就是例如打雷闪电等自然环境所影响的,除了外部噪声,图像噪声也有来自内部干扰的内部噪声,如相机在拍摄时的热噪声、设备本身引起的噪声、电机等。由运动等产生的抖动噪声。
3.2.2 按噪声和信号的关系分类
设f(m,n)表示期望图像信号,则g(m,n)表示加入噪声后的图像,n(m,n)表示噪声。
①加性噪声:图像信号的强弱发生变化时,噪声不会因此改变,他们是不相的关的。不管有没有信号,噪声都存在。在理想的情况下,无噪声图像f、噪声n噪、图像g三者之间的关系应如公式3.1所示:
(3.1)
②乘性噪声:乘性噪声产生的原因一般是由信道之间的关系不理想所引起的,它们与信号之间的关系如公式3.2所示。当图像信号发生强弱变化时,噪声也发生相应的变化,他们是相关的。
g = f + fn噪 (3.2)
3.2.3 按噪声幅度分布的统计特征进行分类
①高斯噪声
如果噪声的概率密度函数能够近似的服从高斯分布则可以称其为高斯噪声。高斯噪声的概率密度函数可以用公式3.1表示:
(3.1)
式中,表示图像的灰度值,u表示期望值,表示的方差。
②瑞利噪声
假设随机变量满足瑞利分布,则其密度函数可以用公式3.2表示如下
(3.2)
其中的均值和方差是:
; (3.3)
③脉冲噪声
如果噪声服从脉冲噪声的特点,则其概率密度函数可以用公式3.4表示如下:
(3.4)
脉冲噪声可以分为两类:一是大气中的雷暴天气产生的电磁脉冲,又称天电干扰,属于自然噪声;另一类是由高频电气设备类似火花系统、电气开关和高压传输线等产生的工业干扰。
3.3 图像噪声的特点
总结概括来说,图像噪声一般具有以下几个特点:
(1)噪声在图像中的体现是随机的,不同的噪声在不同的图像中,其图像分布也是不一样,大小也不一。
(2)图像噪声具有多样性,不同的噪声产生的原因不同,所带来的影响也不同,针对每一种噪声都要运用相对的去噪手段才能良好的去噪。
(3) 噪声和图像通常相互关联。 例如,如果将摄像机信号连接到噪声使其产生图像,实践结果最终表明,越暗的部分噪声越大,越亮的部分其噪声也越低。
(4)噪音具有可增加性。 在串行传输图像的传输系统中,可以发现,将各个组件进行串联后所引起的噪声重叠,致使最终的信噪有所比降低,从而说明图像噪声具有可增加性。
第4章 空域去噪算法及仿真
图像中的诸多噪声均为随机的,其针对某像素点影响可将其当做孤立存在的。基于此,噪声点在对比该像素点临近点中,会在灰度值层面产生明显的改变。基于该情况,可应用邻域操作的模式对图像的像素点有没有噪声进行判定,且应用恰当的方式消除或降低噪声。其中普遍适应的邻域去噪法主要包括了以下几种方法与原理:
4.1 均值滤波法
4.1.1 均值滤波基本原理
均值滤波是一种典型的线性滤波算法,其主要结合了目标像素实现了模板。模板覆盖了周边像素(周边共8像素),形成滤波末班,曲调自身像素,应用该均值取代原本的数值。
4.1.2 均值滤波的缺点
均值滤波自身拥有很大的缺陷,其在图像去噪过程中无法良好的确保图像细节,尤其是细节和边缘区域,图像会转变的比较模糊,无法实现优良的 去噪成效。倘若图像中具备高斯噪声,应用均值滤波可具备极强的去噪成效,但结合椒盐噪声,以上去噪模式不能具备优良的功效。
4.1.2 均值滤波在Matlab中的仿真实现
首先在图像下添加高斯噪声,应用大小各不相同的BOX模板通过均值滤波处置高斯造成图像,其代码具体为下图:
仿真后图像如下
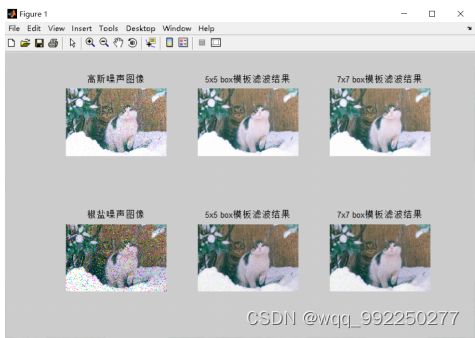
图4.1 均值滤波的滤波效果
由图4.1可以清晰地看出,采用均值滤波虽然有一定的去噪效果,但是会使图像变得模糊。图像去噪成效不但关乎模板形状,还同应用的模板尺寸具备关系。模板具备越大的尺寸,证明具备越明显的去噪成效,但图像会更加的模糊。以上滤波方式针对高斯去噪具备优良的成效,但针对滤除椒盐噪声而言不具备良好的成效。
4.2 中值滤波
中值滤波为经常应用的非线性处理技术,其为邻域运算,经常在预处理中应用。其在平滑脉冲噪声层面具备显著的成效,并且可以良好的对图像尖锐边缘进行保护。其其计算并非加权和,其为将邻域 像素按照灰度值的排序予以重新排列,此后挑选有序序列中间值当做输出像素值。该方式对于干扰脉冲以及椒盐类噪声的抑制是最有效的,可以克服线性平均滤波器所带来的图像细节模糊问题。
图4.2为应用5x5模板针对添加高斯噪声、椒盐噪声的图像予以中值滤波的成效图。在图4.2(a)、(b)可了解到,对椒盐噪声而言,其随机出现了图像的某部分点中,按照中值滤波的相关原理,通过数据排序模式,1亮点噪声点,排序环节会被排放在序列的最右端、最左端,最后挑选有序序列中间区域的值通常并非噪声点值,(基于此可良好的抑制噪声。
中值滤波的代码如下:

仿真后图像如下:
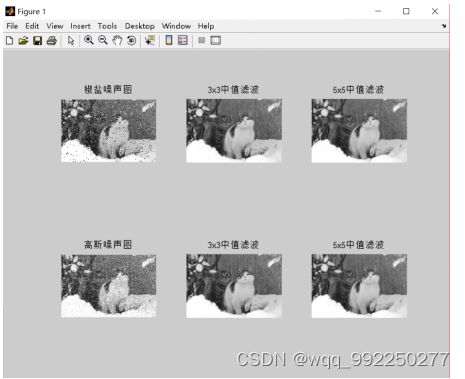
图4.2 中值滤波效果图
运用中值滤波、高斯噪声对比均值滤波,其成效不高,结合椒盐噪声)来说可在去噪过程中良好的保持边缘图像,中值滤波针对去除图像扫描噪声、脉冲干扰十分有效。在真实的应用下,不同图像可应用的需求各不相同,应用不同的滤波窗口尺寸、形状予以滤波。通常首先应用小窗口尺寸,其后挑选大尺寸,实现窗口的逐步增大,直至得到比较满意的去噪效果。
第5章 频域低通滤波
频域滤波是频域图像处理的一种重要方法。从信号的频谱来看,随着空间位置发生变化,变化坡度大的信息所对应的频域是高频部分,而变化平缓的信息所对应的频域是低频部分。通过观测具体的图像可以发现,边缘和噪声对应的频域是高频区域,而背景和信号倾斜部分对应低频区域。因此,可以采用低通滤波来达到滤除噪声的目的。
设F (u,v)和G (u,v)分别为噪声图像F (m,n)和滤波后的输出图像G (m,n)的频域表示,H (u,v)为低通滤波器的传递函数。图5.1为运用离散傅里叶变换频域低通滤波方法进行平滑图像的综合处理流程:

图5.1 频域低通滤波法的原理框图
5.1 几种常用的低通滤波器
5.1.1 理想低通滤波器(ILPF)
理想低通滤波器传递函数定义是:
(5.1)
式中:D0表示通带的半径,D(u,v)为从点(u,v)到频域平面原点的距离。
理想低通滤波器的传递函数曲线及其三维透视图如下所示:
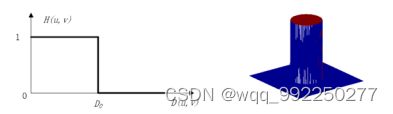
图5.2 理想低通滤波器
低通滤波器通过过滤掉高频的成分导致图像模糊现象的产生,因为该滤波器容易产生急峻的过激反应,从而出现了振铃的情况。
理想低通滤波器可在很大方面降低图像之中的噪声,由于其形成的边缘细节具备明显的模糊效应,在滤波处置后类似平均模板的平滑。
5.1.2 Butterworth低通滤波器(BLPF)
物理可实现低通滤波器巴特沃斯(Butterworth)低通滤波器。N阶、截止频率为D0巴特沃斯低通滤波器传递函数定义是:
(5.2)
或
(5.3)
其对比理想低通滤波一致,D0是截止频率并且其大小是:。
Butterworth低通滤波器,也被叫做最大平坦滤波器,在阻带、通带不具备显著的跳跃,其同理想低通滤波器具备较多的不同,即两者之间的另一个。平滑过渡区。通常,当H(u,v)降低到原始值的1 /√2时,D(u,)被定义为截止点。
图5.3为巴特沃斯低通滤波器的三维透视图、特性曲线。其中低通滤波器具备很大的不同,Butterworth低通滤波器在通带、阻带中拥有平滑过度,拥有很强的非连续的属性。

图5.3 巴特沃斯低通滤波器
通过滤波器函数分析到,过度环节其根本就没有理想低通滤波器的剧烈现状,运用图获得,拥有极强的阶数,滤波器拥有很强的剧烈,拥有特别显著的振铃现状。
5.1.3 指数低通滤波器(ELPF)
在对图像进行处置环节,长期应用的指数滤波器,拥有很快的衰减率,传递函数是:
(5.4)
n是决定衰减率系数。图5.4为指数低通滤波器的三维透视、特性曲线。例如在D(u,v)=D0时候,H(u,v)降低到最大值。
图5.4 指数低通滤波器
与巴特沃斯低通滤波器相比较,相较于指数低通滤波器,其指数函数的过渡带比较平滑,更快衰减率,基于此指数低通滤波之后的图像历经巴特沃斯低通滤波结果比较模糊,没有振铃的情况出现。
5.1.4 梯形低通滤波器(TLPF)
梯形低通滤波器为完全平滑滤波器、理想低通滤波器折中,传递函数为:
(5.5)
D(u,v)=。,在契合D1、D0需要契合条件D0
图5.5为梯形低通滤波器三维透视、特性曲线。其滤波器的主要性能为过渡平稳。
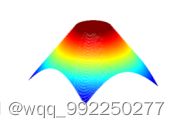
图5.5 梯形低通滤波器
5.2 频域低通滤波在Matlab中进行仿真
以理想低通滤波器为例,给出其Matlab实现程序:

仿真图如下所示:
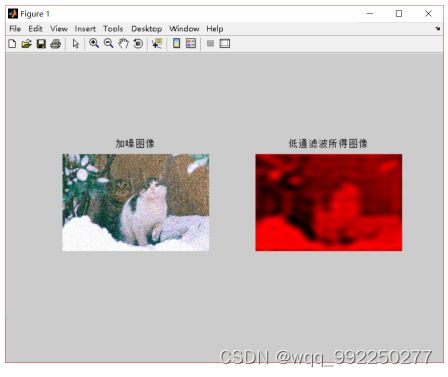
图5.6 理想低通滤波效果图
第6章 图像去噪质量评价
当对图像进行去噪处理之后,处理后的图片没有一个标准的规定来判定图片是否清晰,图像的去噪效果有没有达标。这里我们就需要一个评价标准来衡量去噪后的图像的清晰度以及图像去噪算法的效果。一般来说,可以大致分为主观准则和客观准则两种方法。
6.1 主观判断
表6.1 主观准则评价
评分 评价 说明
A 优秀 图像质量特别好,无任何干扰
B 良好 图像质量高,有少量噪声,但不影响观看
C 一般 图像质量一般,有噪声,但不影响观看
D 及格 图像质量差,有噪声且影响观看
E 差 图像质量差,干扰多且影响观看
F 极差 图像质量极差,无法使用
6.2 客观判断
客观评价为计算图像固定数据,运用数值计算的方式对图像去噪成效进行衡量,评价其有没有实现标准要求。以下文章重点论述了最经常使用的均方信噪比(SNR),并且会在Matlab中对两张去噪后的图像进行对比。
6.2.1 均方信噪比(SNR)
原始的图像加噪后再去噪,其降噪效果可以用SNR大小来衡量。
假设原始图像是f(m,n),去噪之后其图像是(m,n),那么均方误差(MSE)可应用公式6.1表示:
(6.1)
通常而言,具备更小的均方误差,其输出图像综合效果接近原图像,证明具备更好的去噪成效。均方信噪比(SNR)可应用公式6.2进行计算:
(6.2)
对于均方差来说,信噪比则是数值越大代表图像的去噪效果越好,下文中会使用matlab进行仿真对比。
6.2.2 Matlab中计算信噪比
本次仿真对两张图片进行加噪和去噪的处理,然后分别计算信噪比,对比可以体现几种滤波算法对各种噪声的去噪效果。
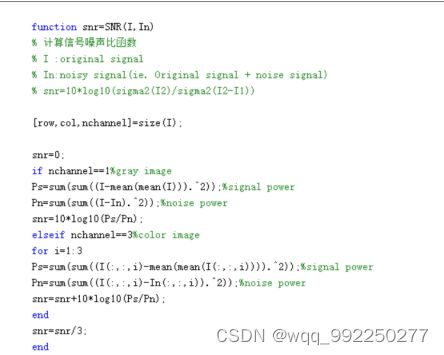
首先在matlab中加入信噪比函数snr.m,输入以下代码:
此后对cameraman.jpg、lena.jpg的图片添加高斯噪声、椒盐噪声,应用均值滤波、中值滤波落实去噪处置,其代码为:

之后分别对两张图片进行仿真以及信噪比的计算,结果如下:
表 6.2 加入高斯噪声后的信噪比
滤波类型 Lena Cameraman
均值滤波 7.2550 9.0124
中值滤波 7.1801 8.8770
表 6.3 加入椒盐噪声后的信噪比
滤波类型 Lena Cameraman
均值滤波 9.3694 11.0128
中值滤波 9.3831 11.1526
根据得出的数据则可以看出,均值滤波针对高斯噪声在去噪过程中其成效比中值滤波更好;针对椒盐噪声,在去噪过程中,中值滤波比均值滤波效果更好。但针对不同图片,结合噪声去噪效果具备诸多不同。
主观评价和客观评价标准都能在一定程度上能够反映出图像去噪后的效果,但是又各自具有不同的特点。主观评价的反映是人眼的直接感受,但是因人而异,这种指标不是以固定量的方式描述,并且有时候人眼觉得好看的图像去噪效果不一定会好。客观评价无法反映出人眼的真实感受,但是是以定量的方式描述,具有一定的严谨性。
第7章 总 结
7.1 总 结
本文对一些常见的去噪算法进行了研究分析与仿真,但是还有多种多样的去噪算法没有提到,每种方法在不同的方面各有优点和缺点,但是没有一种能够完美应对各种情况的去噪算法。
像素平均滤波以及其指定邻域像素的加权平均像素或平均像素的新值,去除突变,以过滤掉噪声,该方法操作简单,速度快,但会导致图像模糊,优化图像细节、边缘,该模式在高斯噪声去除中具备良好的成效,但椒盐噪声的处理效果并不理想。
中值滤波将像素当做重心的小窗口下的全部像素灰度值在小到大进行排序,排序结论中间值当做像素灰度值。其中中值滤波可更好的去除椒盐噪声,并能保持图像边缘的方法,但对高斯噪声效果不佳。
应用低通滤波器落实去噪,可实行将噪声的伪轮廓寄生效应降低到一种极低的状态,由于低通滤波器滤除寄生成分环节与高频成分,基于此原因,以上去噪方式是将降低清晰度当做代价。
由此在针对图像进行去噪过程中,需要对其仔细分析其噪声产生的原因、特点以及类型,并选择最合适的方法进行去噪,这样才能保证图片清晰的同时能够良好地消除噪声。
本设计对其他常见的去噪算法没有进行研究,这是本设计的不足之处。
7.2 展 望
众所周知,图像的特征和噪声自身为去噪难点。当下,接触获得的诸多非线性滤波算法均为特定图像噪声构建的。但是在现实生活中,自然界的多样性和噪声的不确定性会影响整个去噪过程,无法对全部图像落实最好的滤波成效。基于此,不提前了解噪声特性、图像非线性滤波机制获得了大量的使用。伴随科技的迅猛发展,在伺候的发展,图像去噪获得了良好的发展,邻域的使用越发的广泛,必然会给人们的生产、生活产生极大的便利。
参考文献
[1] 章毓晋.图像处理与分析[M].北京:清华大学出版社,1999:23-25
[2] 霍宏涛.数字图像处理[M].北京:机械工业出版社,2003.5:01-02
[3] 李秀梅,张奇伟,应广之.基于Matlab的图像去噪可视化系统设计[J]. 杭州师范大学学报(自然科学版),2012,11(6):551-555.
[4] 王姣斐,王双喜.基于MATLAB软件的图像去噪方法比较[J].甘肃农业大学学报, 2011, 46(4):157-160.
[5] 盛仲飙.基于Matlab的图像去噪算法研究[J]. 河南科学, 2011, 29(10):1218-1220.
[6] 赛地瓦尔地;买买提.基于Matlab的几种图像去噪方法研究[J]. 河南科学, 2013(9):1387-1390.
[7] 白宗文,周美丽.基于matlab的椒盐噪声图像去噪方法研究[J]. 电子测试, 2014(6):27-28.
[8] 刘钰,马艳丽,刘艳霞.小波阈值图像去噪算法及MATLAB仿真实验[J]. 数字技术与应用, 2010(6):122-123.
[9] 王秋雨. MATLAB图像处理的几个应用实例[J].福建电脑, 2011, 27(11):6-7.
[10] Buades A,Coll B, Morel J M. A non-local algorithm for image denoising[C]// IEEE Computer Society Conference on Computer Vision & Pattern Recognition. 2005.
[11] Starck J L, Candès E J, Donoho D L. The curvelet transform for image denoising[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2002, 11(6):670-684.
[12] Beck A, Teboulle M. Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems.[J]. IEEE Transactions on Image Processing, 2009, 18(11):2419-2434.
[13] 王秋雨. MATLAB图像处理的几个应用实例[J]. 福建电脑, 2011, 27(11):6-7.
[14] 彭古. 关于图像去噪和边缘检测的方法研究[D]. 中南大学, 2012.
[15] 基于小波理论的图像去噪和增强技术研究[D]. 武汉理工大学, 2008.
[16] 张然, 汤全武, 史崇升. 基于递推最小二乘自适应滤波算法的图像去噪[J]. 计算机应用与软件, 2014(4):193-196.
[17] 陈晓, 唐诗华. 改进的中值滤波在图像去噪中的应用[J]. 地理空间信息, 2015, 13(6):77-78.
[18] 吕艳鹏, 潘玉田. 基于MATLAB图像处理的非结构化道路识别[J]. 机械工程与自动化, 2014(2):32-33.
[19] 李权, 赵晋芳. 几种图像去噪算法研究[J]. 商丘师范学院学报, 2015(3):27-32.
[20] 王茜.基于自适应阈值的图像去噪方法[J]. 装备制造技术, 2008(8):42-43.
[21] 王文远.基于图像信噪比选择优化高斯滤波尺度[J]. 电子与信息学报, 2009, 31(10):2483-2487.
[22] Luisier F, Blu T. SURE-LET Multichannel Image Denoising: Interscale Orthonormal Wavelet Thresholding[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2008, 17(4):482.
[23] Chang S G, Yu B, Vetterli M. Spatially adaptive wavelet thresholding with context modeling for image denoising[J]. 1998.
[24] Luisier F, Blu T, Unser M. Image Denoising in Mixed Poisson–Gaussian Noise[J]. 2011, 20(3):696-708.
[25] 孟奥, 赵庆军, 徐桓,等. 基于Matlab实现MRI信噪比及图像均匀性自动检测系统的研究[J]. 中国医学装备, 2018, 15(3):29-32.
[26] 袁兴起, 韩键美. 一种基于Matlab的图像滤波算法的设计与实现[C]// 2011中国仪器仪表与测控技术大会论文集. 2011.
致 谢
在毕业设计期间,我遇到许多的难题,在途中遇到许多挫折,很感谢帮助我解答困惑的所有人。在此表示深深的谢意。
首先,我由衷地感谢我的毕业综合训练指导老师李老师。在他悉心的帮助和认真指导下,我顺利地完成了整个毕业设计。在设计过程中,李老师认真负责,专业知识丰富,对我们的各种疑问都做出了正确的解答。
其次,我要感谢和我一起做毕业设计的同学,你们给我提出很多宝贵的意见,在此也真诚的谢谢你们。同时还要感激我的室友们和身旁的朋友,在毕设期间互帮互助,有疑问时互相讨论,互相学习,互相成长。
我还要特别向我的家人表示由衷的感谢,你们是我坚强的后盾,有了你们给我的支持,我才能顺利完成我的学业。
最后,我对在百忙之中抽出宝贵时间来参加论文评阅的各位教师表示由衷的谢意,他们的指导修正了本人论文中的错误,使我受益匪浅。
由于本人学识有限,文中必有不妥之处,敬请各位专家和老师批评指正。