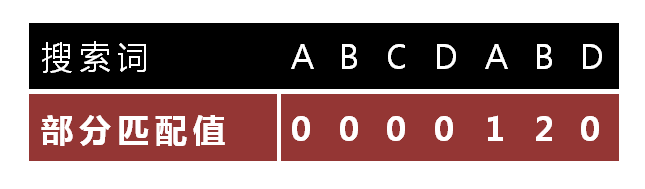数据结构与算法Java(二)——字符串、矩阵压缩、递归、动态规划
不定期补充、修正、更新;欢迎大家讨论和指正
本文以数据结构(C语言版)第三版 李云清 杨庆红编著为主要参考资料,用Java来实现
数据结构与算法Java(一)——线性表
数据结构与算法Java(二)——字符串、矩阵压缩、递归
- 数据结构与算法Java(三)——树
数据结构与算法Java(四)——检索算法
数据结构与算法Java(五)——图
数据结构与算法Java(六)——排序算法
目录
- 字符串
-
- KMP
- 矩阵压缩存储
-
- 对称矩阵
- 稀疏矩阵
- 递归
-
- 汉诺塔问题
- 递归程序执行过程
- 简单递归->非递归
- 复杂递归->非递归
- 回溯
- 动态规划
字符串
字符串是一种特殊的线性表,其元素都为字符,在C语言中,字符串等价于字符数组(字符数组结尾有’\0’作为结束标识),例如"hello"就等价于{ ‘h’, ‘e’, ‘l’, ‘l’, ‘o’, ‘\0’}。
在前面学习线性表后,我们可以实现自己的字符串及相应功能,以下为自己实现的字符串结构MyString,为了方便初始化该类,构造器利用String进行初始化,不然一个个从键盘输入,或用char数组初始化挺繁琐的。
public class MyString {
private static final int M = 20;//字符数组最大容量
private char [] str = new char[M];//字符数组
public MyString(String initStr){
char tmp[] = initStr.toCharArray();
int i;
for (i = 0; i< tmp.length; i++){
str[i] = tmp[i];
}
str[i] = '\0';
}
}
操作集
- int strLength();返回字符串的长度,不包括’\0’
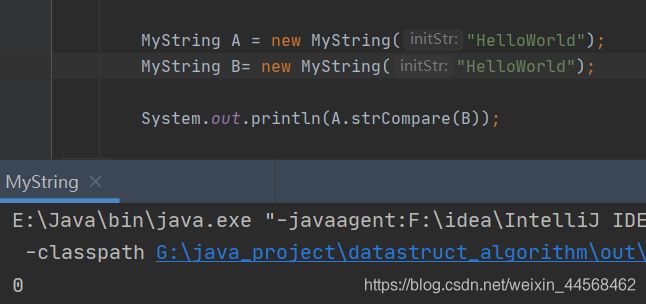
- int strCompare(MyString other);与其他字符串进行比较,如果此字符串结果大于返回1,相等返回0,小于返回-1。(⭐)
- void toUpperCase();将字符串中小写字符转换为大写
- void toLowerCase();将字符串中大写字符转换为小写
- void strDisplay();打印字符串
- boolean isEmpty();判断字符串是否为空
- void strConcat(MyString other);将其他字符串链接到此字符串后边
- MyString subString(int position, int len);从position位置开始截取长度为len的字符作为子串
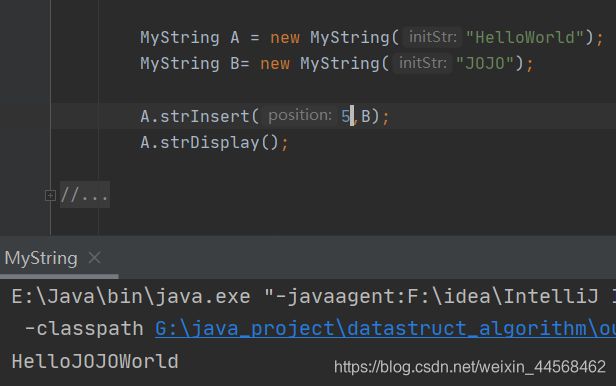
- void strInsert(int position, MyString other);向position位置插入其他字符串。(⭐)
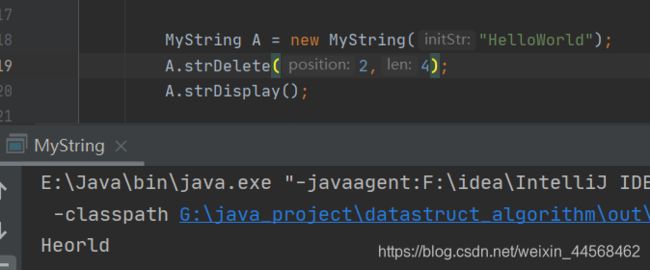
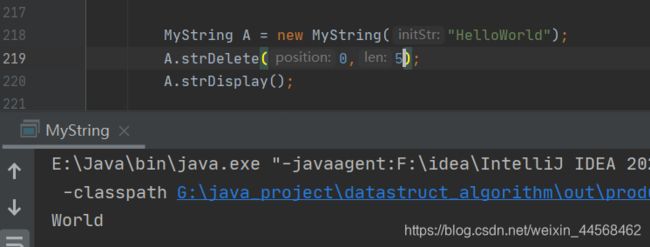
- char[] strDelete(int position, int len);从position位置开始删除长度为len的字符,返回被删除的字符集合。(⭐)
- int index (MyString substr);搜索substr子串在此字符串首次出现的位置,-1表示此字符串没有该子串(⭐)
- int[] KMP(MyString substr);利用快速模式匹配找出子串出现在此字符串所有的位置(⭐⭐)
- void strReplace(MyString sub, MyString replaceText);将此字符串中sub子串替换为replaceText字符串(⭐)
strCompare
public int strCompare(MyString other){
int otherLen = other.strLength();
int thisLen = this.strLength();
if(otherLen<thisLen)
return 1;
else if (otherLen>thisLen)
return -1; //字符串长度不一样可以直接出结果,一样的话就要一个字符一个字符作比较了
else{
for (int i = 0; i<otherLen; i++){
if(this.str[i]>other.str[i])
return 1;
else if(this.str[i]<other.str[i])
return -1;
}
return 0;
}
}
strInsert
实现思想和顺序表插入思想一样,只不过有些小细节需要注意
public void strInsert(int position, MyString other){
int otherLen = other.strLength();//插入字符串的长度
int thisLen = this.strLength();//此字符串的长度
if(position<0||position>thisLen){//判断插入位置是否合理
System.out.println("the position is illegal");
return;
}
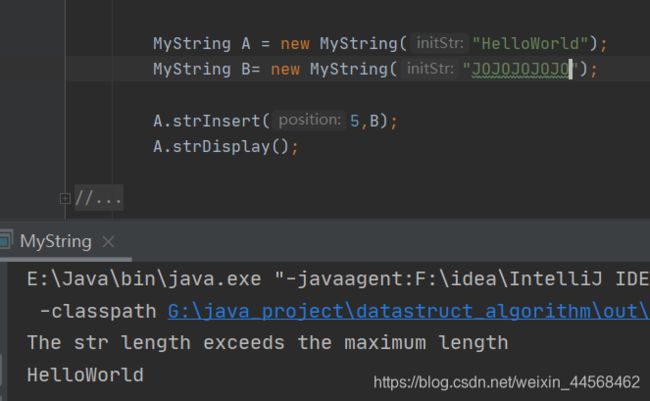
if(otherLen + thisLen > M-1){//判断两字符串加起来的长度是否超过字符数组最大容量,因为结束符'\0',实际上字符串最大有效长度为M-1
System.out.println("The str length exceeds the maximum length");
return;
}
for (int i = thisLen-1; i>=position; i--){
str[i+otherLen] = str[i];//需要腾出otherLen长度的位置,所以下标需要加上otherLen
}
for (int i =0; i<otherLen; i++){
str[position+i] = other.str[i];//将字符串插入空位
}
str[thisLen+otherLen] = '\0';//新字符串末尾加上'\0'标记结束
}
strDelete
public char[] strDelete(int position, int len){
int thisLen = this.strLength();
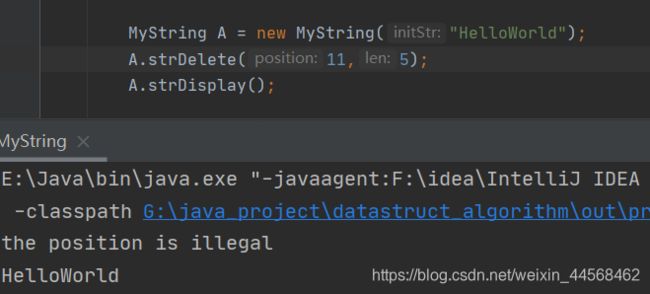
if(position<0||position>=thisLen){//细心的朋友会发现,strInsert判断语句为position>thisLen,这是因为插入可以在末尾后插入,而删除不能
System.out.println("the position is illegal");
return null;
}
if(len<0||len>(thisLen-position)){//比如"hello" 从2(也就是l)开始删除,至多只能删除长度为3字符。即(5-2)=3
System.out.println("the len is illegal");
return null;
}
char tmp[] = new char[len];
for (int i = 0; i<len; i++){//先将要删除的字符保存起来
tmp[i] = str[position+i];
}
for (int i = 0; i<thisLen-position-len+1;i++){//比如"helloworld",从2(也就是l)开始删除4个字符后,需要移动orld\0共5个字符(结束符也得移动),即(10-2-4+1)=5
str[position+i] = str[position+i+len];
}
return tmp;
}
index
public int index (MyString substr){
boolean flag = false;
for (int i = 0; i<=this.strLength()-substr.strLength(); i++){//比如"helloworld",要找出orld长度为4的子串,没必要将数
//组全部遍历完,当遍历到倒数第4个还没对上,后面长度不够就不可能对的上了,即
//(10-4)=6 (str[6]='o', 如果对不上就可以退出了)
if(this.str[i] == substr.str[0]){//遍历主串,直到与子串首位相等后,就可以开始进行匹配了
for (int j = 1; j<substr.strLength(); j++){//因为首位已经相同,从下一位开始比较
if(this.str[i+j] != substr.str[j]){
flag = false;
break;
}
flag = true;
}
}
if (flag)
return i;//返回子串出现位置
}
return -1;//找不到的情况
}
KMP
寻找字符串p(Pattern,模式)在字符串t(Text,正文)中首次出现的起始位置称为字符串的模式匹配,模式匹配在符号处理的许多问题是十分重要的操作。上面实现的index()方法的就是朴素的模式匹配算法,不难发现上述算法的执行效率是十分低的,其时间复杂度为O(nm)(主串循环n次,子串循环m次)。
朴素模式匹配效率低的原因在于,该算法在寻求匹配时没有充分利用比较时已经得到的信息,每次比较不相等时总是将模式p右移,并用p中的字符从头开始再与t中的字符进行比较,这是一种带回溯的比较方法,而这种回溯并不经常是必要的。
而后由D.E.Knuth,J.H.Morris和V.R.Pratt同时发现了一种快速模式匹配算法,称为KMP算法(Knuth-Morris-Pratt)。该算法可以再O(n+m)的时间数量串的模式匹配操作。
KMP算法的描述用文字描述较繁琐且复杂,建议看以下视频和文章了解原理
KMP字符串匹配算法1
字符串匹配的KMP算法
接下来我们以下图为例进行KMP算法的实现

KMP的关键在于构建部分匹配表,一些教材说的next数组和prefix表就是这东西。关于原理同样的看以下视频
public int[] getNext(MyString p){
int len = p.strLength();
int[] next = new int[len];//创建next数组
int j = 0;//j指向前缀的末尾,如果前后缀匹配上,其下标也刚好等于该元素的部分匹配值
int i;//指向后缀的末尾
for ( i = 1; i<len; i++){
while (j>0 && p.str[j] != p.str[i]){//当目前前缀结尾和后缀结尾不相等时,j需要根据前一个元素的部分匹配值进行回溯
//因为回溯过程中可能遇到后缀和前缀部分相等的情况,所以要退出循环
//例如ABCABA,当C和结尾的A不匹配时,经过回溯发现首个A和结尾A是相同的,所以结尾A的部分匹配值为1
j = next[j-1];
}
if(p.str[j] == p.str[i]){
j++;
}
next[i] = j;
}
return next;
}

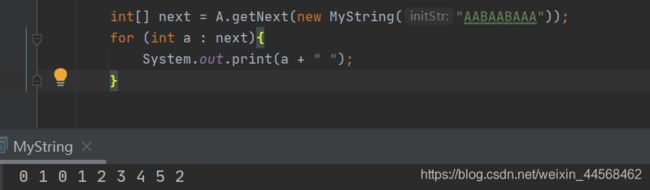
利用next数组就可以进行模式匹配了,可以根据在之前朴素模式算法的基础上进行调正,比较好理解
public int KMP(MyString substr){
int next[] = getNext(substr);//获得next数组
int thisLen = this.strLength();
int subLen = substr.strLength();
boolean flag;
int n = 0;
while (n<thisLen){//用while而不用for是因为主串不用顺序遍历,而是跳着选择遍历
if(this.str[n] == substr.str[0]){//当与子串首元素相同就可以进行匹配了
for (int i = 1; i<subLen; i++){//因为首位已经相同,从下一位开始比较
if(this.str[n+i] != substr.str[i]){
n += i - next[i-1] -1;//下次主串比较的位置,根据next表知道子串要移动的距离,后面还要-1是因为后面有n++
flag = false;
break;
}
flag = true;
}
if(flag)
return n;
}
n++;
}
return -1;
}
利用KMP算法主串的移动只需要5次,比较3次(子串除去首位遍历次数为6),而朴素算法主串需要移动16次,比较4次

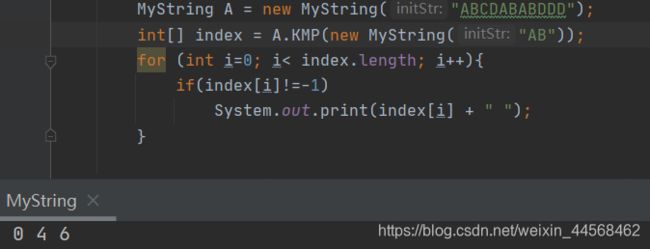
接下来可以对KMP功能做些调整,用来找出子串所有出现的位置,方便接下来实现strReplace函数
public int[] KMP(MyString substr){
int next[] = getNext(substr);
int thisLen = this.strLength();
int subLen = substr.strLength();
boolean flag = false;
int index[] = new int[thisLen];//创建索引表存访子串出现的所有位置,数组长度选择主串的长度,因为极端情况下比如当主串为AAAA,子串为A时,在主串任意处都匹配
int indexPoint = 0;
for (int i = 0;i<thisLen; i++)//初始化索引表,-1表示未找到
index[i] = -1;
int n = 0;
while (n<thisLen){
if(this.str[n] == substr.str[0]){
for (int i = 1; i<subLen; i++){
if(this.str[n+i] != substr.str[i]){
n += i - next[i-1] -1;
flag = false;
break;
}
flag = true;
}
if(flag){
index[indexPoint++] = n;//将匹配位置加入到索引表中
}
}
n++;
}
return index;
}
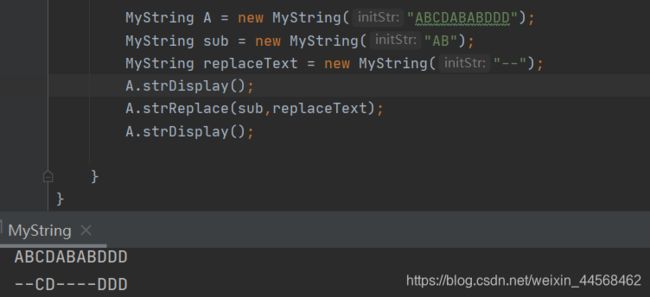
public void strReplace(MyString sub, MyString replaceText){
int index[] = KMP(sub);//利用KMP获取子串出现的位置
int n = 0;
while (index[n]!=-1){//获取有效的位置
n++;
}
int subLen = sub.strLength();
int textLen = replaceText.strLength();
int x = textLen-subLen;//当子串和替换文本长度不同时,需要进一步的操作
for (int i = 0; i<n; i++){
strDelete(index[i],sub.strLength());//先将原子串删除
strInsert(index[i],replaceText);//插入替换文本
index[i+1] += x; //第一个替换的位置肯定是正确的,但是后面的索引表需要更新
x += x;//以ABCDABABDDD为例,替换子串AB,子串出现位置为0,4,6
//更新的规律如下:
//1.替换文本为--,则x=0,索引表位置依然为0,4,6
//2.替换文本为---,则x=1,索引表位置变为0,5,8,
//3.替换文本为-,则x=-1,索引表位置变为0,3,4
//根据规律,无论x为何值(当然要是整数),都在原表基础上加上0*x,1*x,2*x……来进行更新
}
this.str[this.strLength()+n*(textLen-subLen)] = '\0';//重新设置字符串的结尾符
}
矩阵压缩存储
矩阵是许多科学和工程计算问题中研究的数学对象,在高级语言中,矩阵常以二维数组加以表示,但在数值分析过程经常遇到一些特殊的矩阵,它们的阶数很高,但同时矩阵包含许多的值或零,如对称矩阵、三角矩阵、带状矩阵和稀疏矩阵等,如果将它们按照正常矩阵存储的方法必然会浪费许多存储空间,因此要对这些特殊矩阵进行压缩存储,所谓压缩存储即为多个相同值的结点只分配一个存储空间,值为零的结点不分配存储空间。
对称矩阵
对称矩阵(Symmetric Matrices)是指以主对角线为对称轴(这说明对称矩阵是方阵,即行数和列数相同),各元素对应相等的矩阵,如下图两个矩阵。

由于对称矩阵的特性,几乎有一半的值是对应相等的,所以只需要存储对角线以上或以下的部分来节省近一半的存储空间。下面将以下图矩阵为例,进行列优先存储方式来存储对称轴以下的元素。

最后压缩存储的效果如下,16个结点只需要10个存储空间,对于n(n≥1)个结点来说,只需要n(n+1)/2个存储空间。
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 值 | 1 | 3 | -6 | 5 | 2 | 0 | 9 | 4 | -2 | 8 |
通过简单计算和归纳,对于每行的首个结点,其在压缩数组的位置为i(i+1)/2,再根据与首结点的偏移距离就可以求出任意结点的在压缩数组的位置,即i(i+1)/2 + j(当i≥j),j(j+1)/2 + i(当i 如下三角的-2,其下标i = 3, j = 2。通过计算3(3+1)/2 + 2=8;上三角的-2,其下标为i = 2, j = 3。计算得3(3+1)/2 + 2=8,结果相同。 类结构 操作集 compressMatrix() 当然更简便得方法是直接将下三角的结点遍历存储就好 如果一个矩阵中很多元素的值为零,即零元素的个数远远大于非零元素的个数时,称为稀疏矩阵。为了节省存储空间,通常只存储矩阵中的非零元素,但由于稀疏矩阵中非零元素的部分不像前面那些矩阵呈现一定的规律性,因此存储非零元素时必须增加一些附加信息加以辅助。 稀疏矩阵如果采用顺序存储方法一般包括:三元组表示法、带辅助行向量的二元组表示法和伪地址表示法。 接下来将以下图为例(具体实现稍有点出入,元素的下标仍然以0开始,三元组表的首行记录稀疏矩阵的信息) compressMatrix 十字链表中,同一行的所有非零元素串成一个带表头的环形链表,同一列的非零元素也串成一个带表头的环形链表,且第i行非零元素链表的表头和第i列非零元素链表的表头共用一个表头结点,同时所有表头结点也构成一个带表头的环形链表 因此十字链表中有两类结点:非零元素结点和表头结点。 程序调用自身的编程技巧称为递归( recursion)。递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量,同时采用递归技术设计的算法具有结构清晰,可读性强,便于理解的优点。但由于递归执行过程中,伴随这函数自身的多次调用,因而执行效率较低,所以后面需要考虑将递归转换为非递归的方式。 递归的形式分为两种: 如果函数A的定义中包含对B的调用,B的实现又包含A的调用,则为间接递归,如 现在来具体看一个用递归实现的例子——斐波那契数列 注意:根据上面的公式定义,n是从0开始,所以n=5时并不是第5项而是第6项 综上所述,递归程序设计具有两个特点 汉诺塔问题是递归算法的经典问题,法国数学家爱德华·卢卡斯曾编写过一个印度的古老传说:在世界中心贝拿勒斯(在印度北部)的圣庙里,一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候,在其中一根针上从下到上地穿好了由大到小的64片金片,这就是所谓的汉诺塔。不论白天黑夜,总有一个僧侣在按照下面的法则移动这些金片:一次只移动一片,不管在哪根针上,小片必须在大片上面。僧侣们预言,当所有的金片都从梵天穿好的那根针上移到另外一根针上时,世界就将在一声霹雳中消灭,而梵塔、庙宇和众生也都将同归于尽。 当金片为1片,n=1时,从第一根柱子移动到第三根柱子只需要移动m=1次 后来学者们发现一种出人意料的简单方法,只要轮流进行两步操作就可以了。 同样的n=1时,m=1 当n>1时,我们可以把任意多的金片想象成只有两片金片——底层一块大的n(A)=1,剩下的视为一块小的n(a) = n-1。 在n=2情况下,大金片只需要移动1次,而小金片移动2次,因此总共移动m=m(A)+2m(a) 那么m(a)等于多少呢,a同样的可以视为由底层大金片和剩下的小金片组成,继续套娃下去,直到金片只剩一个知道移动确切的次数。到这就已经是很直观的递归思想了。 由于递归调用是对函数自身的调用,在依次函数调用未终止之前又开始了另一次函数调用,按照语言关于作用域的规定,函数的执行在终止前其所占用的空间是不能回收的,这意味着函数自身每次不同的调用需要分配不同的空间。为了对这些空间有效的管理,系统内部设立了一个栈,用于保存每次函数调用与返回的各种数据,主要包括函数调用执行完成时的返回地址、函数的返回值、每次函数调用的实参和局部变量。以下为具体过程 当被调用函数返回时, 现在我们来看没有返回值递归程序执行过程 在第一行打印1个1,在第2行打印2个2,在第3行打印3个3……在第n行打印n个n print(5)的执行由(1)、(2)两部分顺序执行,而(1)中print(4)的执行又有(3)、(4)两部分组成……直到(9)和(10)。 如图,实线表示调用动作,虚线表示返回动作(教材和上面实现的有点小差异,因为教材首项是从1开始,了解意思就行) 采用递归方式实现的程序具有结构清晰、可读性号、易于理解等优点,但一般而言较之于非递归程序无论是空间还是时间的要求都更高,因此在希望节省存储空间和追求执行效率的情况下,人们更希望使用非递归方式实现问题的解决。 一般而言,求解递归问题又两种方式,一种直接求值,无需回溯,这类我们称之为简单递归问题;另一种递归问题求解过程中不能直接求值,必须进行时探和回溯,这类则为复杂递归问题。 根据前面的学习可知,要使用递归机制实现问题的算法程序,其前提必须是使用分划技术,将求解的问题分化成若干和原问题结构相同,但规模较小的子问题,这样可以使原问题的解建立在子问题解的基础上,而子问题的解又建立在更小的子问题解的基础上。由于问题的求解是从原问题开始的,因此递归的求解方式为自顶向下产生计算序列的方式。 而非递归方式采用的是递推技术,递推技术同样以分划技术为基础,也同样需要求解问题分划成若干与原问题结构相同但规模较小的问题,但不同的递推方法是采用自底向上的方式产生计算序列,其首先计算规模最小的子问题的解,在此基础上依次计算规模较大的子问题的解,直到最后产生原问题的,这种方法也就是算法里比较重要的动态规划(Dynamic Programming,DP) 比如斐波那契数列,就是没有回溯的简单递归问题,我们可以以前两项为基础,利用循环依次求出后续第任意项的值 递归方式的思路可以这样:首先先将数组中下标为left+1到right-1的所有元素进行逆转,最后再进行下标为left和right的进行交换,而下标为left+1和right-1的实现过程完全相同,只是所处理的对象范围不同。 非递归方式就不说了 简单递归问题求解过程中,无需试探和回溯,因而通过递推技术就可以实现,然而大多数的递归问题均为复杂递归问题,其在求解过程中无法保证动作一直向前,往往需要设置一些回溯点,当求解无法进行下去或当前处理的工作已经完成时,必须退回到所设置的回溯点继续求解,因此常使用栈的特性来记录和管理所设置的回溯点。 先看一个简单的例子 按中点优先的顺序遍历线性表问题,首先输出线性表中点位置上的值,然后输出中点左部所有元素的值,再输出中点右部所有的值;例如 采用递归的思路十分简单,我们先输出表中点值后,将左部和右部视为另两张新表,按照同样规律递归输出即可 首先先定义栈的结构,用于存储数组的起始位置(左)和结束位置(右)public class SymmetricMatrix {
private static final int N = 4;
private static int[][] matrix = new int[N][N];
static{
matrix[0][0] = 1; matrix[0][1] = 3; matrix[0][2] = 5; matrix[0][3] = 9;
matrix[1][0] = 3; matrix[1][1] = -6; matrix[1][2] = 2; matrix[1][3] = 4;
matrix[2][0] = 5; matrix[2][1] = 2; matrix[2][2] = 0; matrix[2][3] = -2;
matrix[3][0] = 9; matrix[3][1] = 4; matrix[3][2] = -2; matrix[3][3] = 8;
}
}
public int[] compressMatrix(){
public int[] compressMatrix1(){
int m = N*(N+1)/2, n;
int [] tmp = new int[m];
for (int i = 0; i< matrix.length; i++){
for (int j = 0; j< matrix[0].length; j++){
if(i>=j)
n = i*(i+1)/2 + j;
else
n = j*(j+1)/2 + i;
tmp[n] = matrix[i][j];
}
}
return tmp;
}
public int[] compressMatrix(){
int m = N*(N+1)/2, n = 0;
int [] tmp = new int[m];
for (int i = 0; i< matrix.length; i++){
for (int j = 0; j<=i; j++){
tmp[n++] = matrix[i][j];
}
}
return tmp;
}

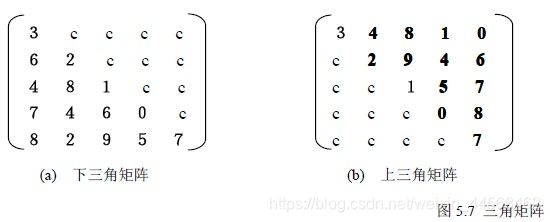
三角矩阵是方形矩阵的一种,因其非零系数的排列呈三角形状而得名。 三角矩阵分上三角矩阵和下三角矩阵两种。 上三角矩阵的对角线左下方的系数全部为零或常数,下三角矩阵的对角线右上方的系数全部为零或常数,如下图。三角矩阵的压缩跟对称矩阵的压缩差不多,自行实现。
稀疏矩阵
其中三元组表示法最常用,其表现形式为(i, j, value),i为非零元素所在的行号,j为非零元素所在的列号,value为非零元素的值,除此之外还需要记录稀疏矩阵的行数、列数和非零元素的总个数(刚好也为三个,可以用三元组表示,放在压缩数组的首行)。
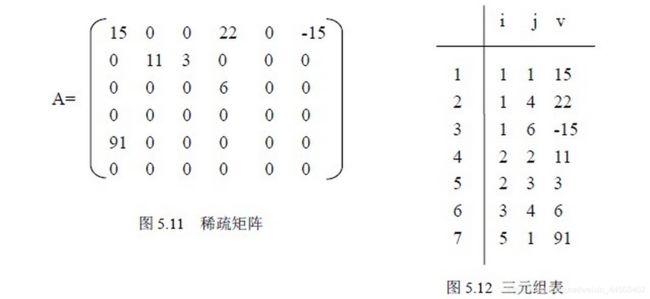
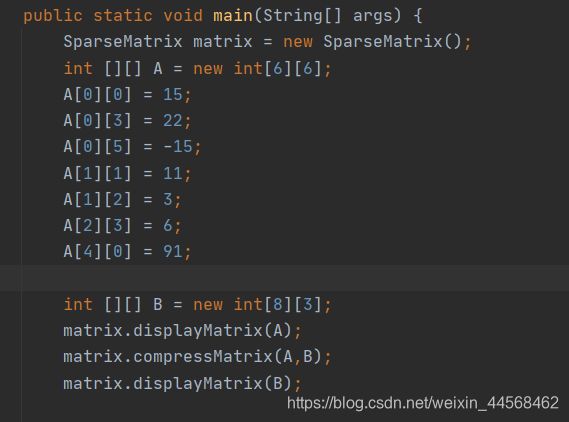
操作集
public void compressMatrix(int [][] pre, int [][] after){
int num = 0;
for (int i = 0; i<pre.length; i++){
for (int j = 0 ; j<pre[0].length; j++){
if(pre[i][j]!=0){
num++;
after[num][0] = i;
after[num][1] = j;
after[num][2] = pre[i][j];
}
}
}
after[0][0] = pre.length;
after[0][1] = pre[0].length;
after[0][2] = num;
}
public int[][] resumeMatrix(int [][] pre){
int [][] matrix = new int[pre[0][0]][pre[0][1]];
for (int i = 0; i< matrix.length;i++){
for (int j = 0; j< matrix[0].length; j++){
matrix[i][j] = 0;
}
}
for (int i = 1; i<pre.length; i++){
matrix[pre[i][0]][pre[i][1]] = pre[i][2];
}
return matrix;
}
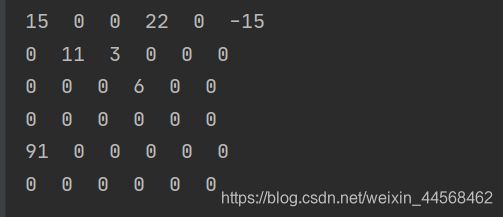
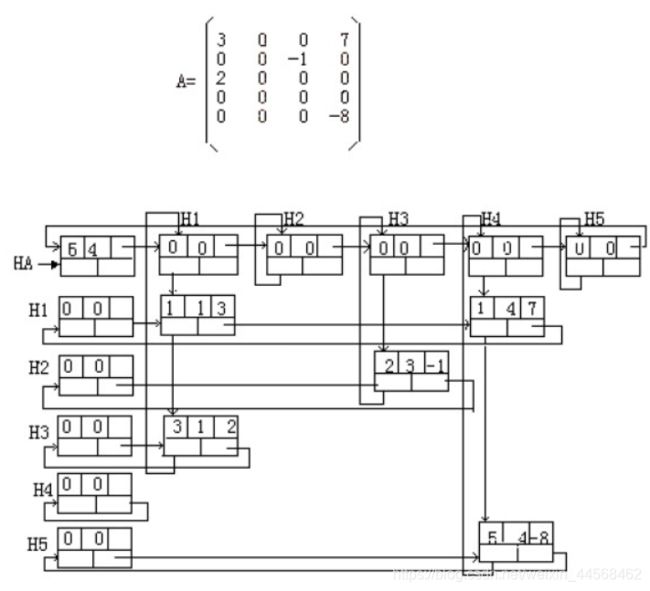
以上采用的是顺序存储三元组表示法,链式存储实现主要包含:带行指针向量的单链表表示法、行-列表示法和十字链表表示法,这里只介绍十字链表表示法。
为了程序实现方便,两者结构都包含五个域:行域(row)、列域(col)、值域(val)或指针域(next)、指向同列下一个非零元素的指针域(down)、指向同行下一个非零元素的指针域(right),如下图。
如果是非零元素结点,row和col分别记录的是该结点所在的行数和列数(因为有头结点,所以下标从1开始),val记录的是该结点的值
如果是表头结点,row和col都设置为0,因为表头结点没有数据域,所以可以将val改为指向本表头结点的下一个表头结点的指针域next。
最后是整个链表的总表头,其row和col分别记录矩阵的总行数和总列数,next域指向第一个表头结点

下图为实际例子
递归
如果一个函数的定义中出现了对自己本身的调用,称为直接递归,如public void A(){
...
A;
...
}
public void A(){
...
B;
...
}
public void B(){
...
A;
...
}
斐波那契数列是意大利数学家莱昂纳多·斐波那契(Leonardo Fibonacci)定义的数列,这个数列从第3项开始,每一项都等于前两项之和
![]()
归纳公式如下
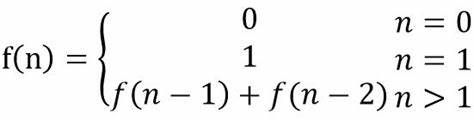
根据公式可知,当n>1时,第n项级数的值等于第n-1项和第n-2项级数的值相加,而第n-1项和第n-2项级数值的求解又分别取决于它们各自的前两项之和。总之f(n-1)和f(n-2)的求解过程与f(n)的求解过程相同,只是具体形参不同。利用以上的性质,进行程序设计时便可以使用递归技术实现public static int Fibonacci(int n){
if(n==0){
return 0;
} else if(n==1){
return 1;
}else {
return Fibonacci(n-1) + Fibonacci(n-2);
}
}
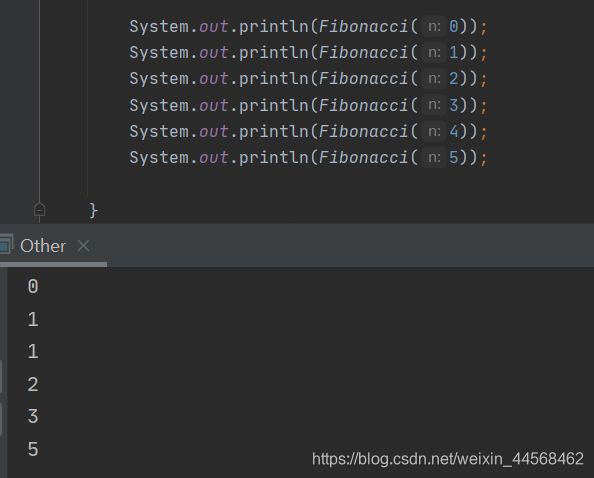

由以上例子可以看出来,要使用递归技术进行程序设计,首先必须要将要求解的问题分解成若干子问题,这些子问题的结构与原问题结构相同,但规模较原问题小。递归程序在执行过程中,通过不断修改参数进行自身调用,将子问题分解成更小的子问题进行求解,知道最终分解成的子问题可以直接求解为止,因此递归程序设计时需要有个终止条件,否则递归将无休止地进行下去。
汉诺塔问题

假如每秒钟移动一次,根据计算得需要移动 18446744073709551615 次,这表明移完这些金片需要5845.42亿年以上,而地球存在至今不过45亿年,太阳系的预期寿命据说也就是数百亿年。真的过了5845.42亿年,不说太阳系和银河系,至少地球上的一切生命,连同梵塔、庙宇等,都早已经灰飞烟灭。
n=2时,需要将小的移动到第二根柱子,大的随后移动到第三根柱子,最后小的移动到第三根柱子,总共移动m=3次
n=3时,也就是上图,总共移动m=7次
n=4时,m=15
n=5时,m=31次
……
通过归纳可以发现,当盘子的个数为n时,移动的次数应等于2ⁿ - 1 (n>0),但没用上递归的思想。
因为A固定为一片,所以m(A)=1,而a由剩下的n-1金片组成,所以还不知道移动多少次,这样移动次数m = 1+2m(a)public static int Hanoi(int n){
if(n==0)
return 0;
else if(n==1)
return 1;
else
return 2*Hanoi(n-1) + 1;
}
递归程序执行过程
public static void print(int n){
if(n!=0){
print(n-1);
for (int i=1; i<=n; i++){
System.out.print(n+ " ");
}
System.out.println();
}
}
由于(9)中的执行print(0)时,n=0满足递归的终止条件,递归将不再继续下去,而是下来执行(10),当(10)结束,意味着(7)中的print(1)完成,进而可以开始执行(8)……直到(2)完成后print(5)的执行才结束,所以函数最后的输出结果由(10)、(8)、(6)、(4)、(2)部分的输出结果顺序组成。

该例子没有函数的返回值,因此其执行过程相对比较简单,我们以斐波那契数列来看看由返回值的递归程序执行过程
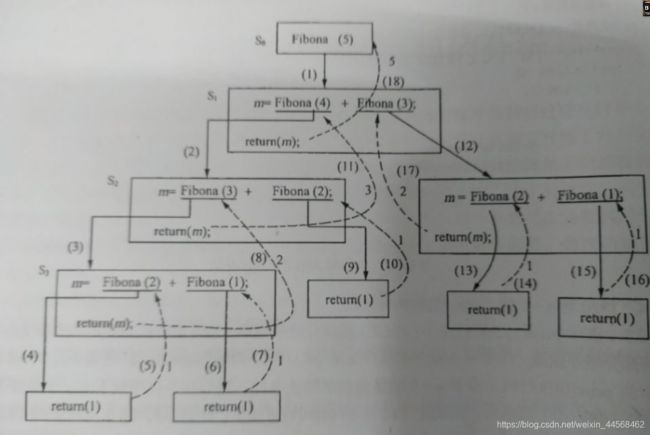
简单递归->非递归
public static int Fibonacci1(int n){
int first = 0, second = 1, third = 1 ;
if(n == 0)
third = 0;
for (int i = 2; i<=n; i++){
third = first + second;
first = second;
second = third;
}
return third;
}

我们来看时间差距,可以看出两者之间有十分巨大的差距(刚开始以为算错了,后面试验把非递归加到4百万项才花费7ms,而递归算法到100项已经卡住了)
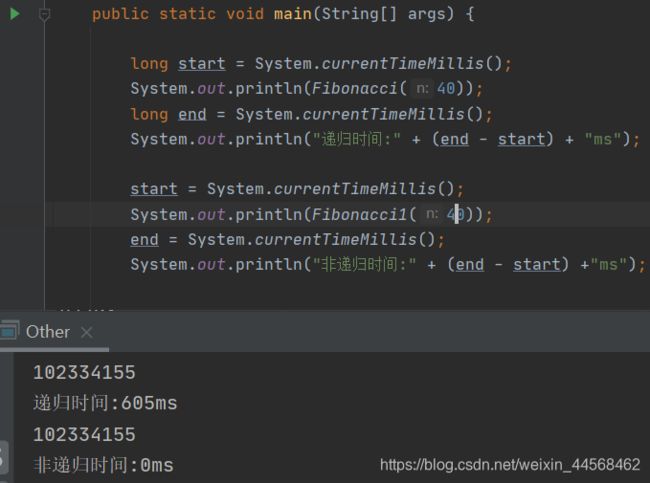
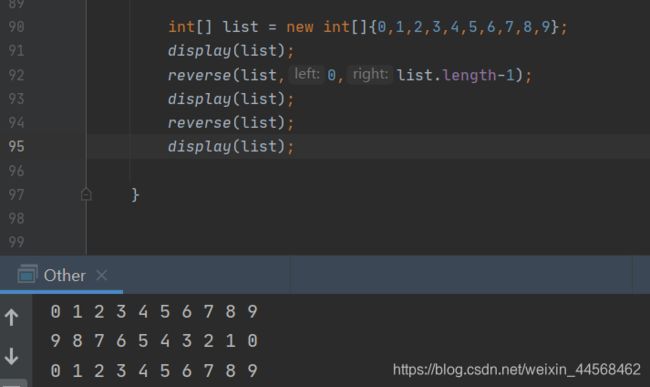
下面再看一个例子,实现顺序表所有元素的逆转public static void reverse(int[] list, int left, int right){
if(left<right){
reverse(list,left+1,right-1);
int tmp = list[left];
list[left] = list[right];
list[right] = tmp;
}
}
public static void reverse(int[] list){
int left = 0, right = list.length-1;
while (left<right){
int tmp = list[left];
list[left] = list[right];
list[right] = tmp;
left++;
right--;
}
}
复杂递归->非递归
18 42 4 9 26 6 10 30 12 8 45
输出结果应为
6 4 18 42 9 26 12 10 30 8 45public static void listOrder(int [] list, int left ,int right){
int mid;
if(left<=right){
mid = (left+right)/2;
System.out.print(list[mid] + " ");
listOrder(list,left,mid-1);
listOrder(list,mid+1,right);
}
}

而使用非递归方式实现,再遍历输出中点值后,中点将线性表分为左半部分和右半部分,根据题目要求,进行左半部分遍历前需要将右半部分先保存起来,以便访问完左半部分所有元素后,再进入右半部分访问,因此要在此设置一个回溯点,入栈保存,而终止条件就是栈空或者左指针大于右指针,没有回溯点,表示所有元素均已输出。static class Node{
int l;
int r;
public Node(int l, int r) {
this.l = l;
this.r = r;
}
}
public static void listOrder(int [] list){
Node[] stack = new Node[list.length];
int top = 0, left = 0, right = list.length-1, mid;
while (left<=right || top!=0){//当正在处理的数据段不为空或栈不为空
if (left<=right){
mid = (left+right)/2;
System.out.print(list[mid] + " " );
stack[top++] = new Node(mid+1, right);//记录右边部分的起始位置和结束位置
right = mid - 1;
}else {//当数据段为空时进行栈顶进行回溯
top--;
left = stack[top].l;
right = stack[top].r;
}
}
回溯
动态规划