详解二叉树

【本节目标】

• 1.树的概念和结构

• 2.二叉树的概念和结构

• 3.二叉树的顺序结构及实现

• 4.二叉树的链式结构及实现

---

1.树的概念及结构

1.1树的概念

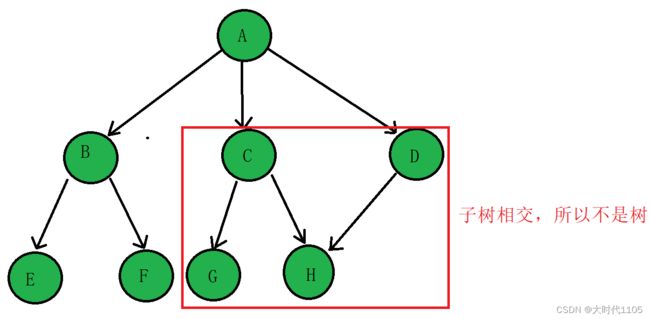
树是一种非线性的数据结构，它由一个根结点和n(>=0)个子树构成，之所以叫做树，是因为它很像生活中的树倒过来的样子

注意：

• 子树是不相交的
• 每个结点有且只有一个父结点

---

1.2树相关的概念：

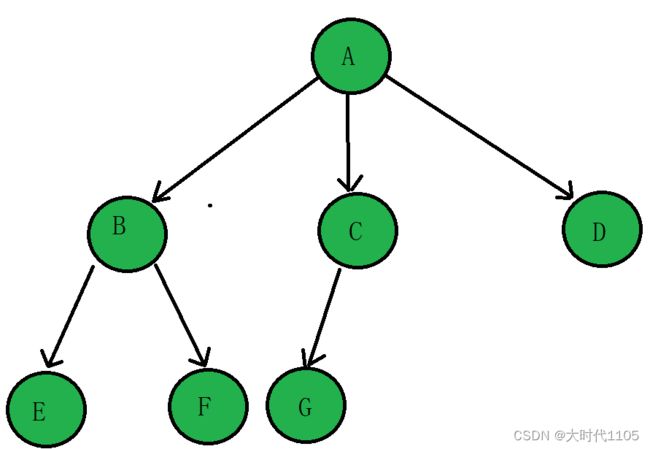
结点的度：一个结点拥有孩子的个数就叫该结点的度，比如A的度为6，E的度为0；

叶结点或终端结点：度为0的结点就是叶结点，比如B，H，I，J......就是叶结点

分支结点或非终端结点：度不为0的结点就是分支结点，比如A，C，D......就是分支结点

父结点：若一个结点含有子节点，则称该结点为其子结点的父结点，比如A就是B的父结点

子结点：一个结点其子树的根结点称为该结点的子结点，比如B就是A的子节点

兄弟结点：两个结点的父节点是同一个结点称为这两个结点是兄弟结点，比如I和J就是兄弟结点

树的度：一颗树中所有结点的度中最大值就是树的度，比如上面的树的度是6

结点的层次：从根结点开始定义，根为第一层，往下依次递增，比如I结点所在的层次为3

树的高度或深度：树中结点的最大层次，比如上面的树的高度为3

堂兄弟结点：两个结点的父结点在同一层，并且这两个结点不为兄弟结点，称这两个结点为堂兄弟结点，比如H和I是堂兄弟结点

结点的祖先：从根结点到该结点的路径上所有的结点都叫该结点的祖先，比如I的祖先是A和D

子孙：以某结点为根的子树下，所有的结点都是该节点的子孙，比如所有的结点都是A的子孙

森林：m(>0)颗互不相交的树的集合叫做森林

---

1.3树的结构

• 由于每个结点我们并不知道它有几个子节点，可以定义一个指针数组，规定了每个结点有SIZE个子节点

typedef int TreeDataType;

#define SIZE 5

struct Node
{
	TreeDataType val;
	struct Node* a[SIZE];
};

这样定义的问题是，实际上每个结点的子节点树是不确定，有可能某些结点的子节点没有SIZE个，就造成了空间的浪费

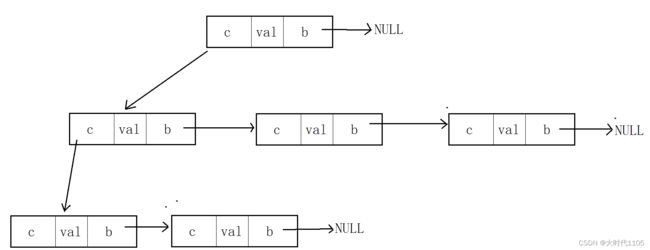
在使用中，我们更常用名为左孩子右兄弟的结构表示法：

typedef int TreeDataType;

typedef struct Node
{
	TreeDataType val;
	struct Node* leftChild;
	struct Node* rightBrother;
}Node;

---

2.二叉树的概念和结构

2.1二叉树的概念

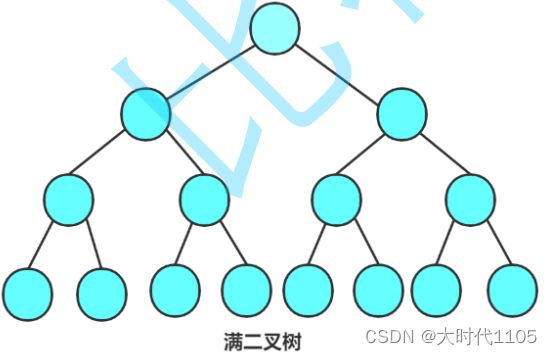
度数<=2的树叫做二叉树

1. 

2.2特殊的二叉树

1. 满二叉树：一个二叉树，如果每一层的结点数都达到最大值，也就是说，如果一个高度为h的二叉树，它的总结点数为，则称该二叉树为满二叉树
2. 完全二叉树：一个二叉树的高度为h，如果它的前h-1层是满二叉树，且h层的结点从左到右是连续的，则称该二叉树为完全二叉树

2.3二叉树的性质：

规定二叉树的层数从1开始

1. 一颗非空二叉树，第i层最多有个结点
2. 深度为h的二叉树最多有个结点
3. 一颗满二叉树，有N个结点，它的高度是
4. 一颗完全二叉树，有N个结点，它的高度范围是
5. 对于任何一颗二叉树，如果它度数为0的结点的个数为，度数为2的结点的个数为，则
6. 若将一个二叉树从上到下，从左到右按照数组的方式依次编号，则父结点和子结点之间的关系：
   1）假设父结点的下标为i，由父结点算子结点：左孩子为2*i+1，右孩子为2*i+2
   2）假设子结点下标为j，由子结点算父结点：父结点为(j-1)/2

2.4二叉树的存储结构

二叉树的存储结构由两种：

1.顺序结构存储

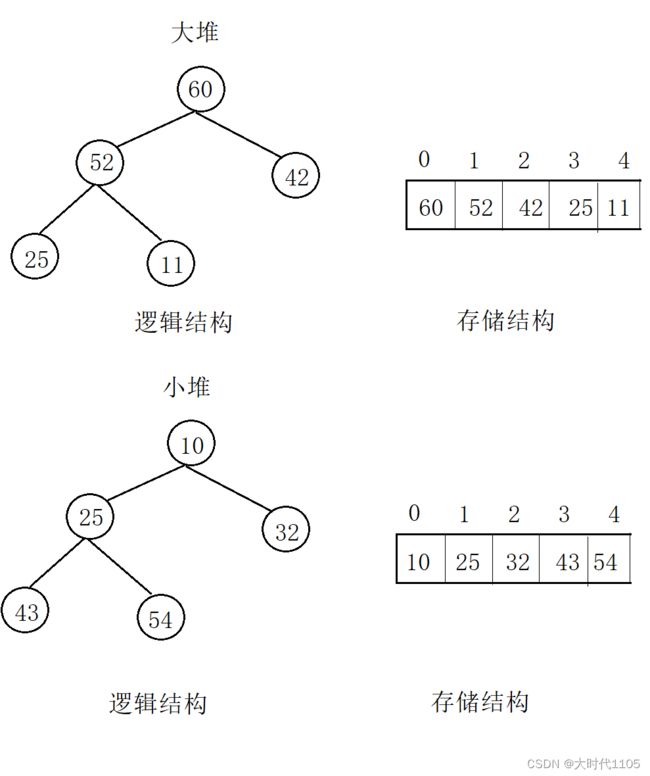
所谓用顺序结构存储，就是用数据存储，但是用数组存储的二叉树最好是满二叉树或完全二叉树，因为这两个二叉树的结点是连续的，正好与数组连续相对应；如果是普通的二叉树用数组存储，数组中间有的位置需要空出来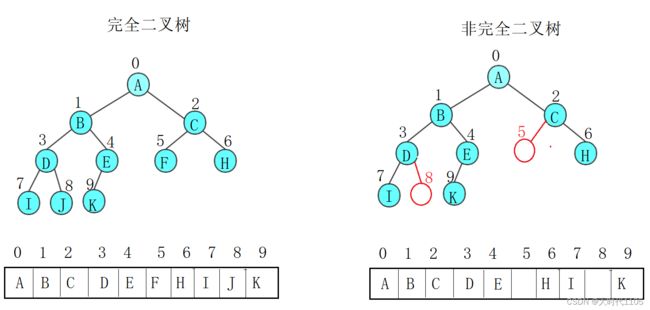

2.链式结构存储

链式结构存储就是用链表将数据串起来；通常有二叉链，三叉链，二叉链是一个结点中两个指针，一个指针指向左子树，另一个指向右子树；而三叉链在二叉链的基础上又加了一个指向父节点的指针，目前我们只考虑二叉链。

结构定义：

//二叉链
typedef int BTNDataType;

typedef struct BinaryTreeNode
{
	BTNDataType val;//值
	struct BinaryTreeNode* leftChild;//指向左孩子
	struct BinaryTreeNode* rightChild;//指向右孩子
}BinaryTreeNode;

---

2.5二叉树顺序结构的应用

2.5.1堆的概念

• 堆是一种完全二叉树，分为大堆和小堆
• 由于完全二叉树的特性，堆中的数据适合用数组来进行存储

2.5.2堆的性质

• 大堆中，所有父结点均大于子结点；小堆中，所有父结点均小于子结点

2.5.3堆的实现

结构定义：

• 前面说过，堆适合用数组存储，因此我们堆的结构就类似一个顺序表

typedef int HeapDataType;

typedef struct Heap
{
	HeapDataType* a;
	int size;//有效数据个数
	int capacity;//容量
}Heap;

---

实现接口：

//初始化
void HeapInit(Heap* php);

//销毁
void HeapDestroy(Heap* php);

//入数据
void HeapPush(Heap* php, HeapDataType x);

//出数据
void HeapPop(Heap* php);

//判空
bool HeapEmpty(Heap* php);

//获取堆顶数据
HeapDataType HeapTop(Heap* php);

//获取堆的数据个数
int HeapSize(Heap* php);

---

初始化：

//初始化
void HeapInit(Heap* php)
{
	assert(php);

	php->a = NULL;
	php->capacity = php->size = 0;
}

---

入数据：

我们以大堆为例，小堆同理

• 假设入数据前，我们的数据是一个大堆，此时入的数据有两种情况：
  1）入的数据比其父结点大：那么为了保持大堆的性质，我们得将其和其父结点交换；如果此时该数据还比其父结点大，那么还要进行交换，直到比其父结点小或其成为根结点
  2）入的数据小于等于其父结点：此时就相当于尾插，不需要动数据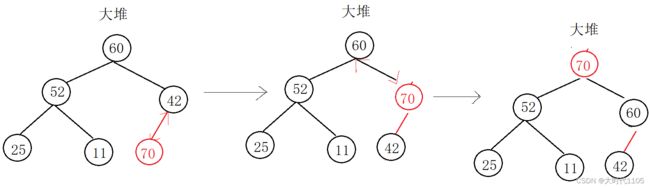

我们把插入的数据往上调整的过程叫做向上调整算法

向上调整算法的实现：

•  如果孩子比父亲大，则交换两者，再更新孩子和父亲，直到父亲大于孩子或孩子成为根结点

void Swap(HeapDataType* p1, HeapDataType* p2)
{
	HeapDataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

//向上调整算法
void AdjustUp(HeapDataType* a, int child)
{
	int parent = (child - 1) / 2;

	while (child > 0)
	{
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (parent - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

//入数据
void HeapPush(Heap* php, HeapDataType x)
{
	assert(php);

	//判断是否需要扩容
	if (php->capacity == php->size)
	{
		int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HeapDataType* tmp = (HeapDataType*)realloc(php->a, sizeof(HeapDataType) * newCapacity);
		if (tmp == NULL)
		{
			perror("HeapPush:realloc fail");
			exit(-1);
		}
		php->capacity = newCapacity;
		php->a = tmp;
	}

	php->a[php->size] = x;
	php->size++;

	AdjustUp(php->a, php->size - 1);
}

---

出数据：

很多人会想，出数据不就是size--吗？在之前的顺序表，链表等数据结构中，出数据的确就只是移除数据；但是，到了这个阶段，我们得考虑到，出数据不仅仅是为了出数据了，要进一步想，我做这个操作有什么作用？

在堆中，如果出数据就只是移除堆尾的元素，那出了数据有什么意义呢？

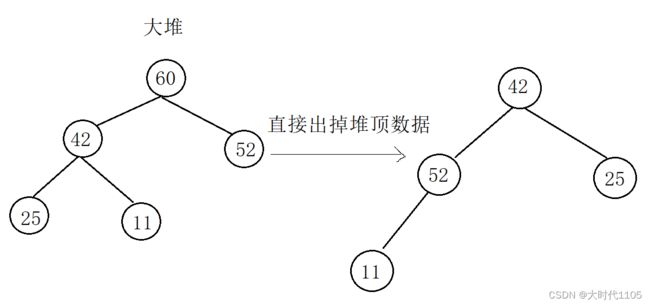
因此，在堆中，我们的出数据是出掉堆顶的数据，那这样做有什么意义呢？根据堆的性质，堆顶的数据是数组中的最大值(最小值)，将最大值(最小值)删除，接下来就可以筛选次大值(次小值)了......往下一一筛选，是不是就能降序(升序)我们的数据

那么是不是直接出掉堆顶的数据呢？如果直接出掉堆顶的数据，此时所有结点的父子关系都乱了，且此时的二叉树不一定是一个堆了；因此，我们出数据的操作是，先将堆顶数据和堆尾数交换，再出掉堆尾数据，就相当于出掉堆顶数据，且此时根结点的子树的关系不变

• 此时的二叉树有可能不是大堆，但其子树肯定都是堆，需要我们调整，我们将根结点向下调整叫做向下调整算法

向下调整算法：

• 我们需要将孩子当中较大的那个与父亲交换，按照常规写法，需要先将其中一个孩子与父亲比较，如果孩子大于父亲，则交换，否则和另一个孩子比较；要求我们写两个逻辑，但这两个逻辑的本质又是一样的，就显得有些冗余，于是想到我们之前写过的假设法
  先假设比较的孩子为左孩子，如果右孩子大于左孩子，则将待比较的孩子换成右孩子
• 如果孩子大于父亲，则交换，之后更新孩子和父亲，直到孩子小于父亲或者孩子越界了
• 有种特殊情况，孩子正好在堆尾，此时比较右孩子和左孩子时，右孩子越界了；应当控制一下比较的条件
  

void AdjustDown(HeapDataType* a, int size, int parent)
{
	int child = parent * 2 + 1;

	while (child < size)
	{
		if (child + 1 < size && a[child + 1] > a[child])
		{
			child++;
		}

		if (a[parent] < a[child])
		{
			Swap(&a[parent], &a[child]);
			parent = child;
			child = child * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

因此我们的出数据代码就是：

//出数据
void HeapPop(Heap* php)
{
	assert(php);

	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;

	AdjustDown(php->a, php->size, 0);
}

---

判空：

//判空
bool HeapEmpty(Heap* php)
{
	assert(php);

	return php->size == 0;
}

---

获取堆顶数据：

//获取堆顶数据
HeapDataType HeapTop(Heap* php)
{
	assert(php);

	return php->a[0];
}

---

获取堆的数据个数：

//获取堆的数据个数
int HeapSize(Heap* php)
{
	assert(php);

	return php->size;
}

---

销毁：

//销毁
void HeapDestroy(Heap* php)
{
	assert(php);

	free(php->a);
	php->a = NULL;
	php->capacity = php->size = 0;
}

想要排序数据：

void TestHeap()
{
	int a[] = { 3, 4,7,2,1,8,9,22,73,24 };
	Heap hp;
	HeapInit(&hp);
	for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++)
	{
		HeapPush(&hp, a[i]);
	}

	while (!HeapEmpty(&hp))
	{
		HeapDataType ret = HeapTop(&hp);
		printf("%d ", ret);
		HeapPop(&hp);
	}
	printf("\n");
}

 

---

2.5.4堆的应用

堆的常见应用：

1. 堆排序
2. TOPK问题

上面我们用堆的插入和删除操作完成了数据的排序，但实际上改变的只是堆里面的数据，对外面的a数组并没有改变，当然了，我们也可以在最后拷贝到原数组；但其实不需要那么麻烦，在下篇博客，我将会讲讲堆真正强大的功能——堆排序

还有一个非常经典的问题，在N个数据中，取出最大的前K个数：

我们常见的思路是，将该数据弄成一个大堆，然后再PopK次

时间复杂度是：，也就是，好像效率也还行

但如果N取非常大，10亿，甚至100亿呢？此时我们的内存是存不下这么多数据的，这些数据只能放在文件中，此时我们的思路是：

1. 先取数据中的前K个数据，将这K个数据建小堆，再将后面的数据依次跟堆顶数据比较，如果大于堆顶数据，就替换堆顶数据进堆，再调整成小堆
2. 依次往后比较，最后比完的这K个数就是最大的前K个数

可能有人疑惑的是为什么是建小堆，如果是建大堆，由于大堆的性质，堆顶的数是最大值，如果这N个数中的最大值在第一次建堆时进去了，那么后面比较时就没有数据比堆顶数据更大，我们的堆就不能完成更新；只有建小堆，堆顶的数据是这K个数中最小的，那么最大的前K个数一个会将其他数排挤出去

时间复杂度：

具体代码的实现也会在下篇博客详解

需要堆的实现的源码的小伙伴可以去我的Gitee主页获取

Heap/Heap · baiyahua/LeetCode - 码云 - 开源中国 (gitee.com)